Trong lịch trình Toán học tập lớp 10, các em học sinh được học không ít kiến thức mớ lạ và độc đáo về đại số cùng hình học. Kì thi cuối năm sắp tới đây mà nhiều người học sinh vẫn cảm thấy choáng ngợp trước lượng kiến thức và kỹ năng mà các em đề xuất học và chần chừ phải ôn tập bắt đầu từ đâu. Hiểu được điều đó, loài kiến Guru đã biên soạn tài liệu tóm tắt những công thức toán lớp 10 dành bộ quà tặng kèm theo cho các bạn học sinh.
Bạn đang xem: Tổng hợp kiến thức toán lớp 10
Tài liệu tóm tắt một cách đầy đủ và gọn ghẽ nhất những công thức toán vẫn học theo hai phần đại số cùng hình học. Hy vọng, đây sẽ là cẩm nang nhỏ tuổi gọn mà không thiếu thốn kiến thức để các em ôn tập giỏi và để dành ôn lại cho trong thời gian học tiếp theo sau khi quên.

I, bí quyết toán lớp 10 phần Đại số
1. Các công thức về bất đẳng thức:
+ đặc thù 1 (tính chất bắc cầu): a > b và b > c
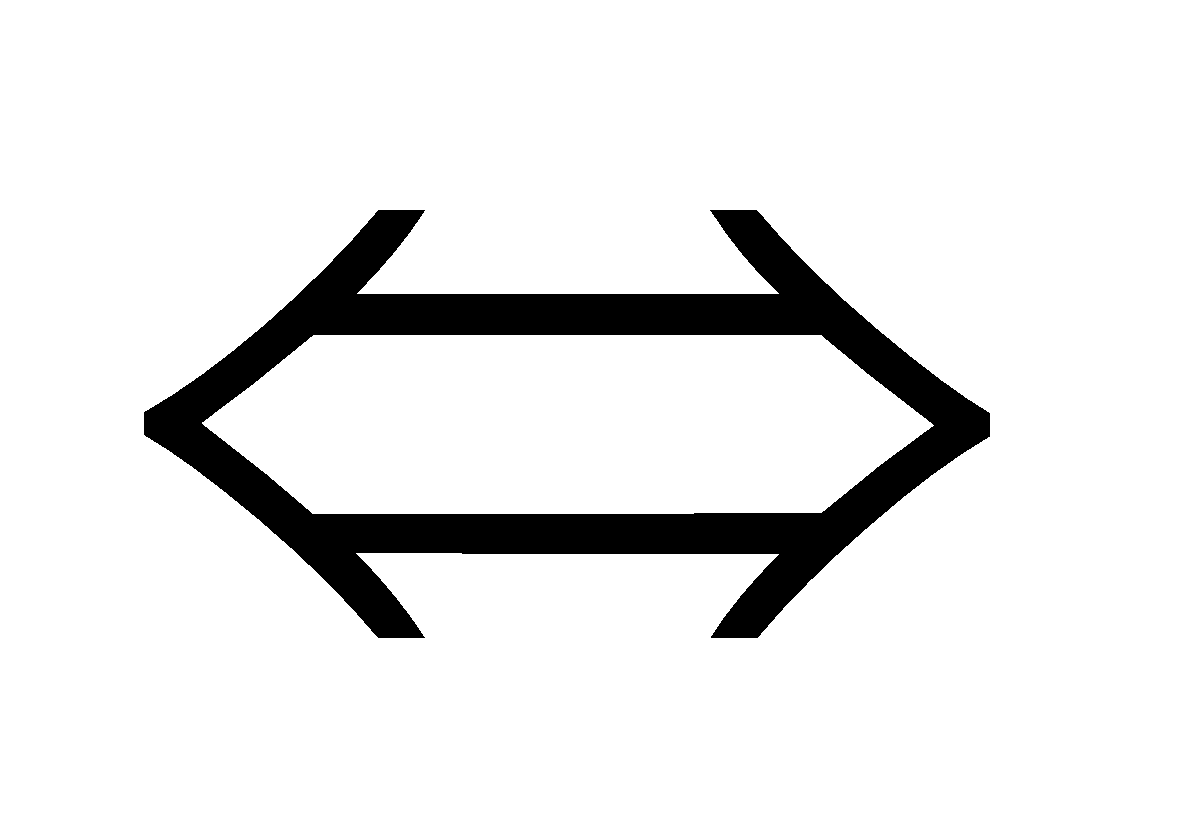
+ đặc điểm 2: a > b
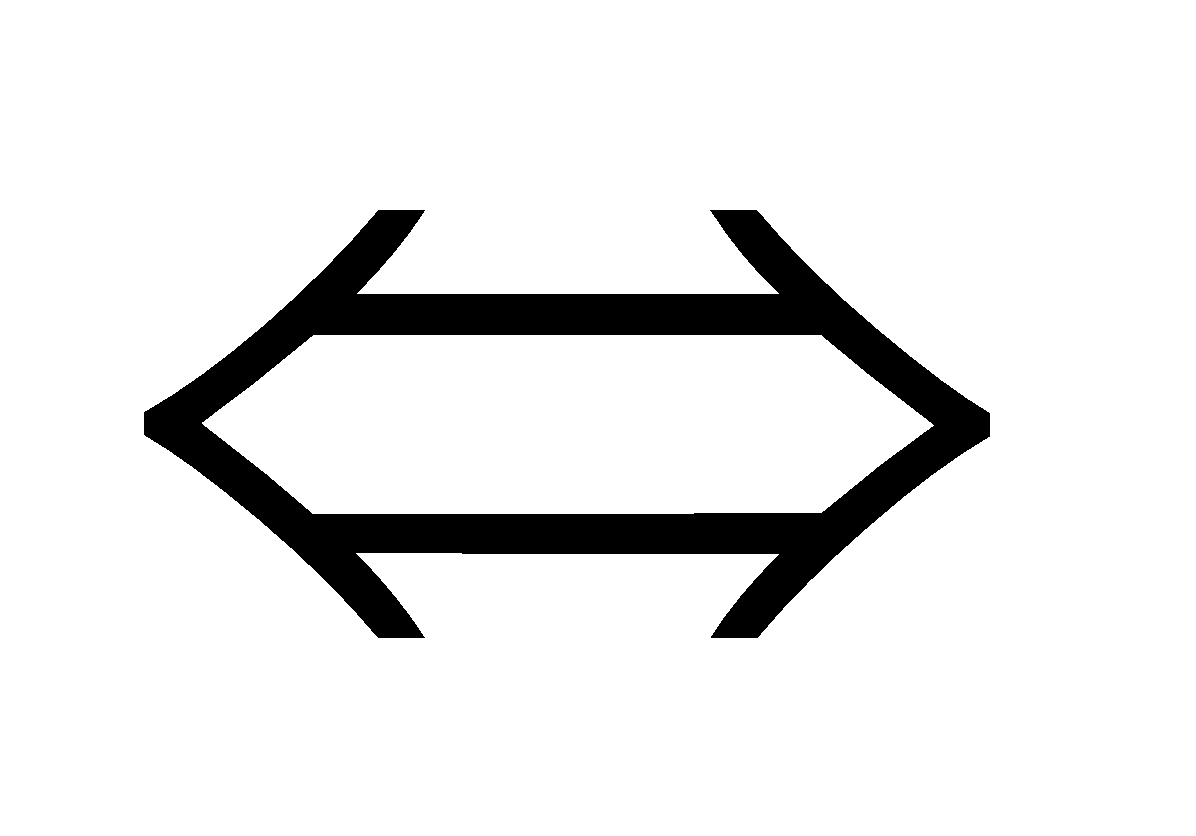
Tức là: Nếu cộng 2 vế của bắt đẳng thức với cùng một trong những ta được bất đẳng thức cùng chiều và tương đương với bất đẳng thức sẽ cho.
Hệ quả (Quy tắc chuyển vế): a > b + c
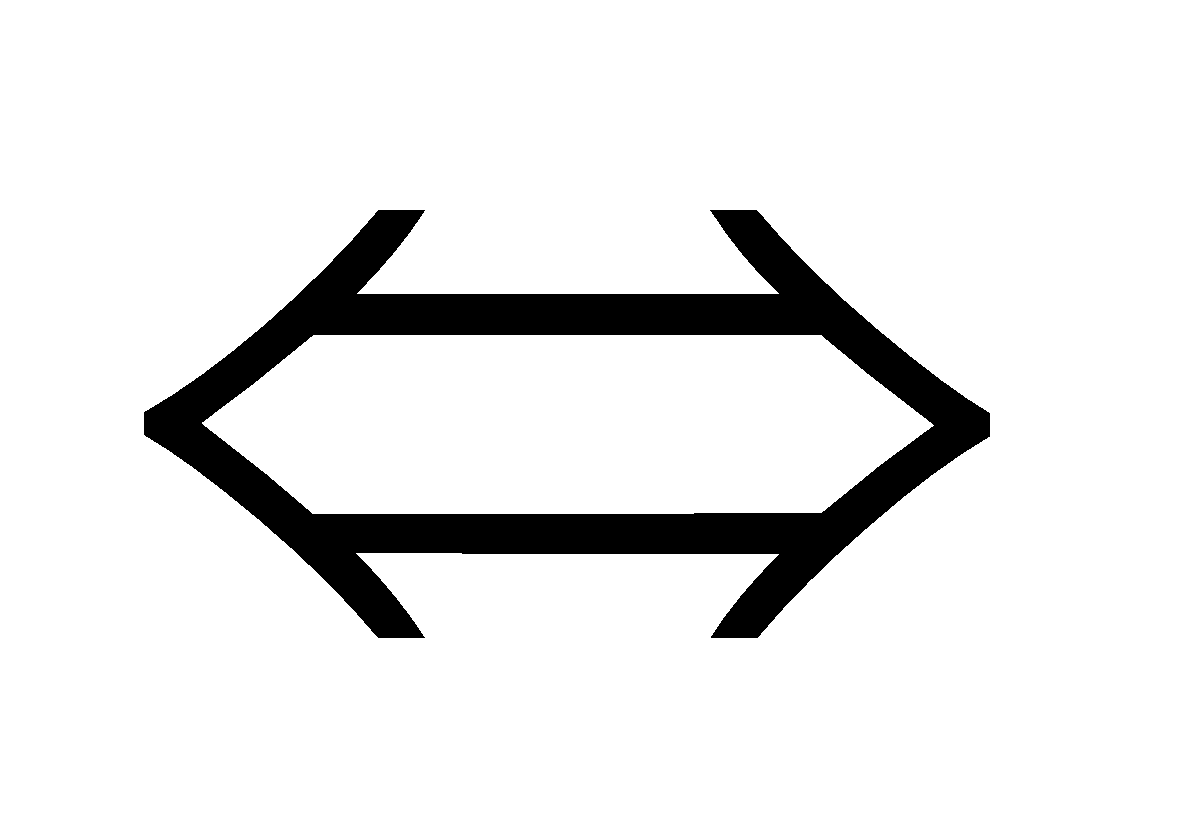
+ đặc thù 3:
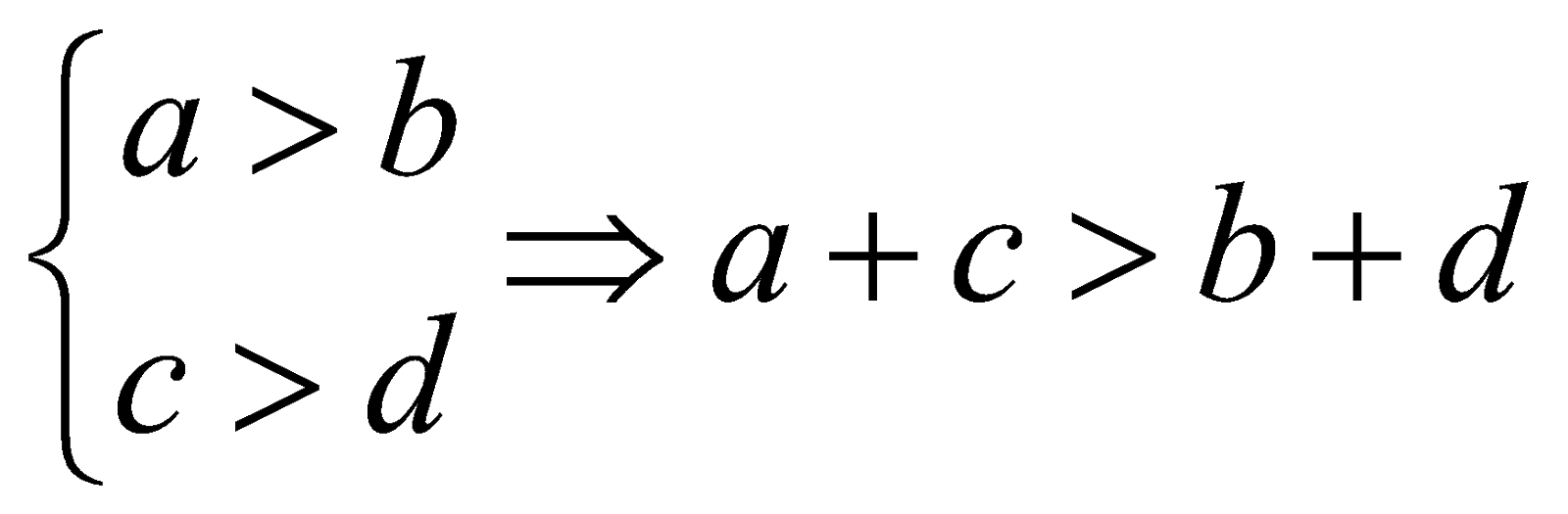
+ đặc điểm 4:
a > b
hoặc a > b
+ đặc điểm 5:
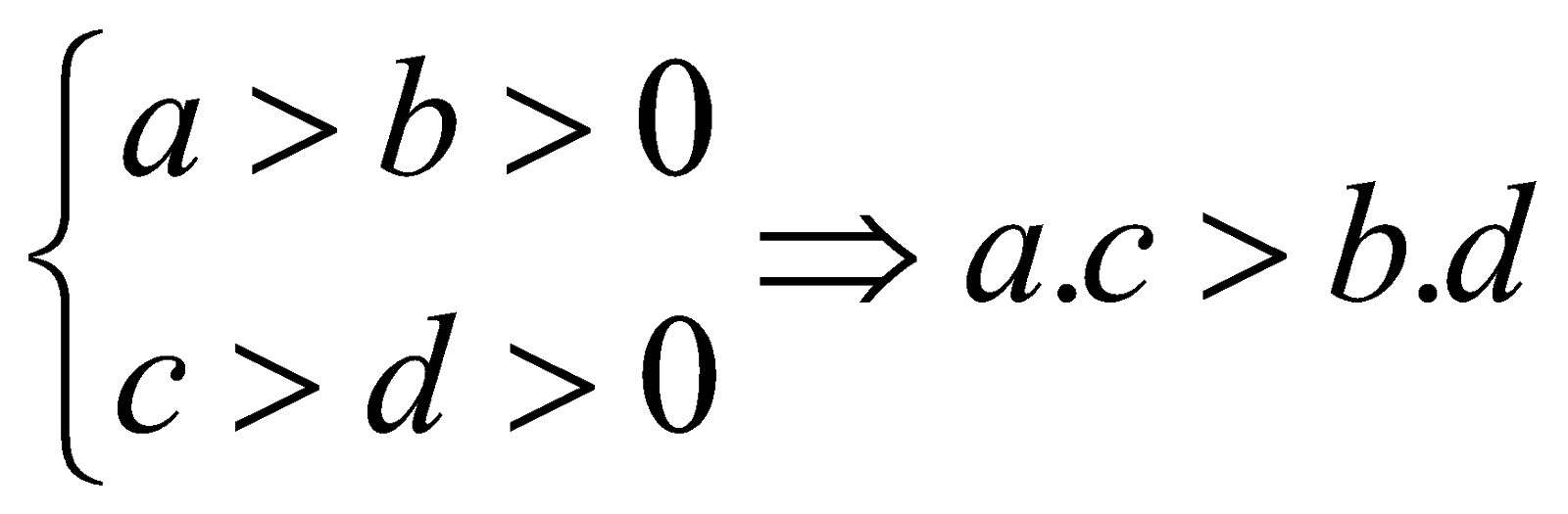
Nếu nhân những vế tương xứng của 2 bất đẳng thức thuộc chiều ta được một bất đẳng thức cùng chiều. Chú ý: KHÔNG gồm quy tắc phân tách hai vế của 2 bất đẳng thức thuộc chiều.
+ đặc thù 6:
a > b > 0

+ đặc thù 7:
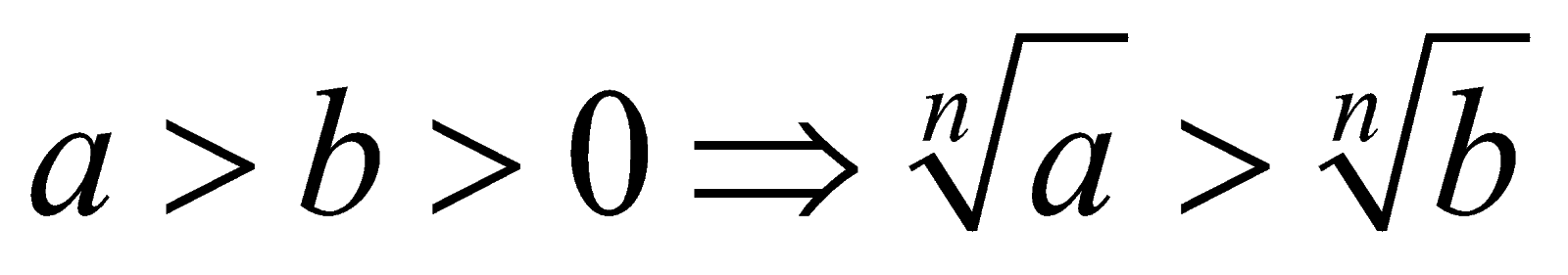
+ Bất đẳng thức Cauchy (Cô-si):
Nếu
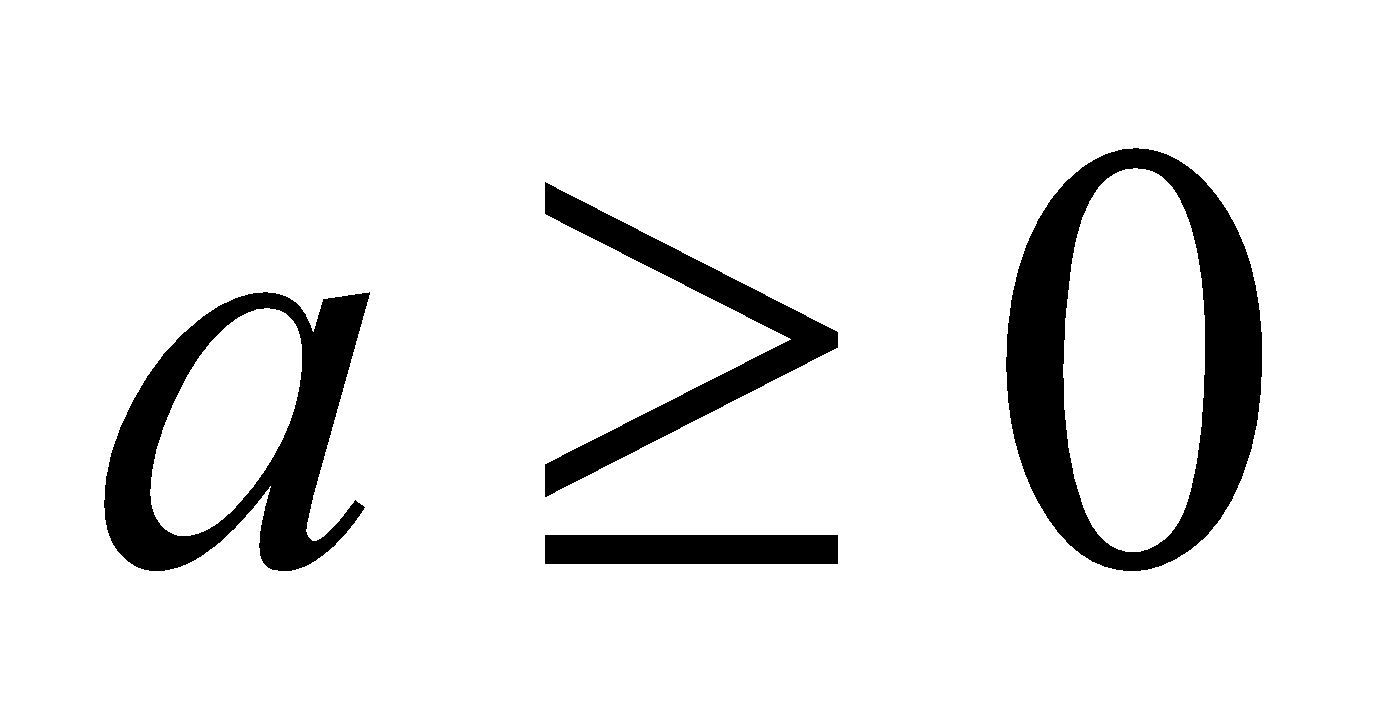

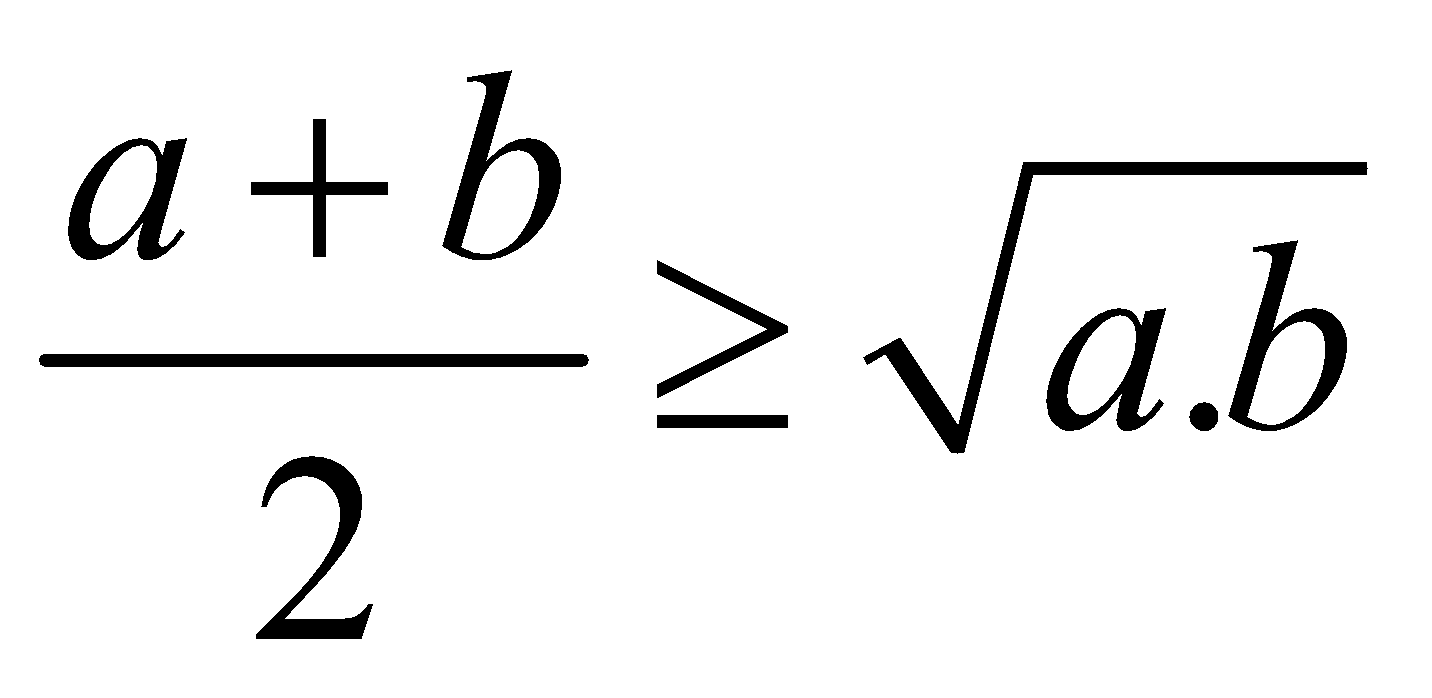
Tức là: Trung bình cùng của 2 số không âm to hơn hoặc bởi trung bình nhân của chúng.
Hệ quả 1: giả dụ 2 số dương bao gồm tổng không đổi thì tích của chùng lớn nhất khi 2 số đõ bẳng nhau.
Ý nghĩa hình học: Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích s lớn nhất.
Hệ quả 2: nếu 2 số dương gồm tích không đổi thì tổng của chùng nhỏ dại nhất lúc 2 số đó bởi nhau.
Ý nghĩa hình học: Trong tất cả các hình chữ nhật tất cả cùng diện tích hình vuông vắn có chu vi nhỏ nhất.
+ Bất đẳng thức cất giá trị trị xuất xắc đối:
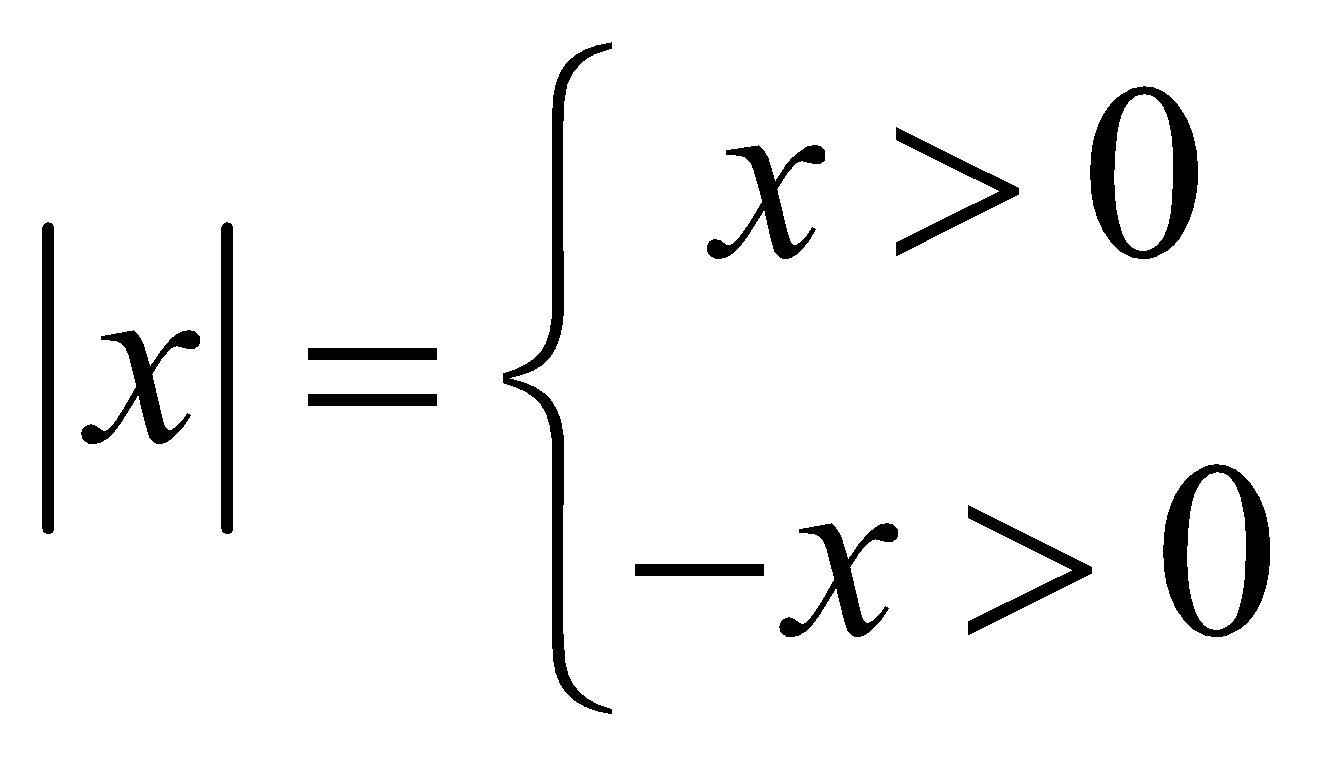
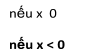
Từ khái niệm suy ra: với tất cả

a. |x|
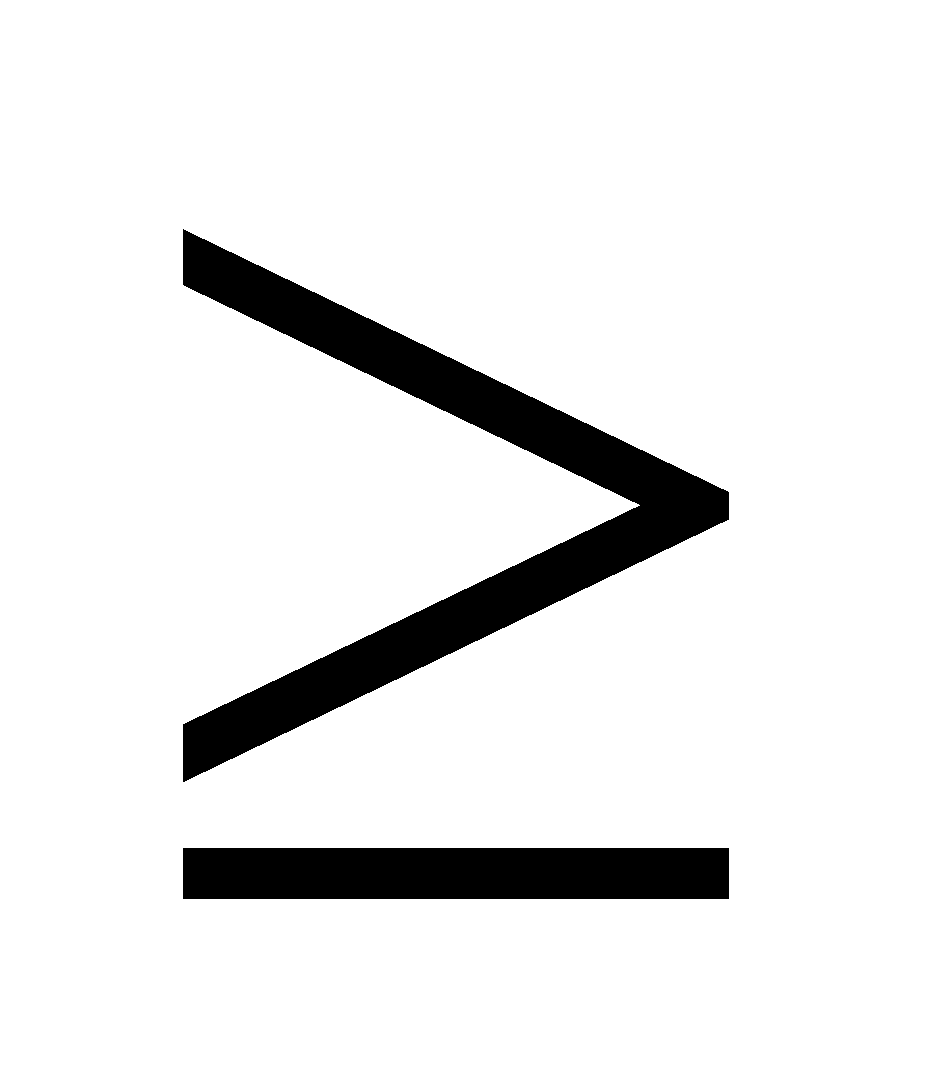
b. |x|2 = x2
c. X
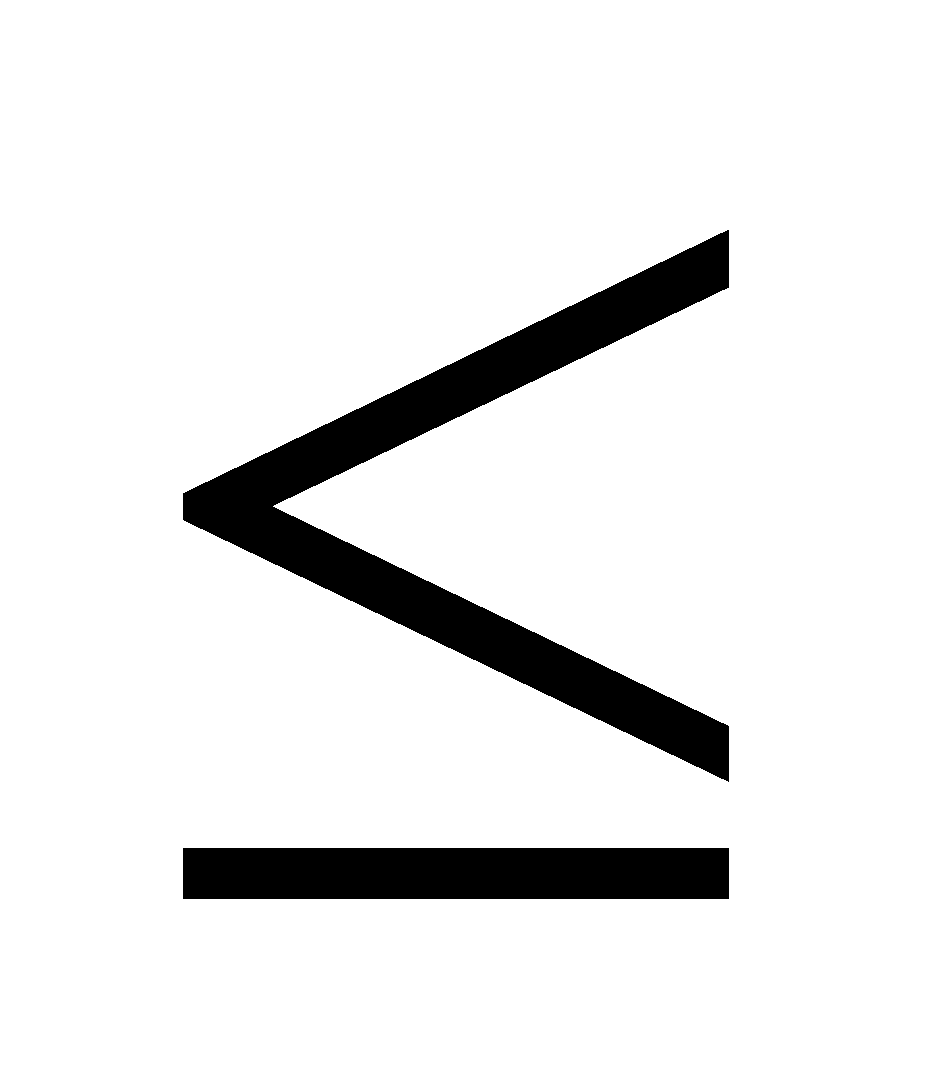
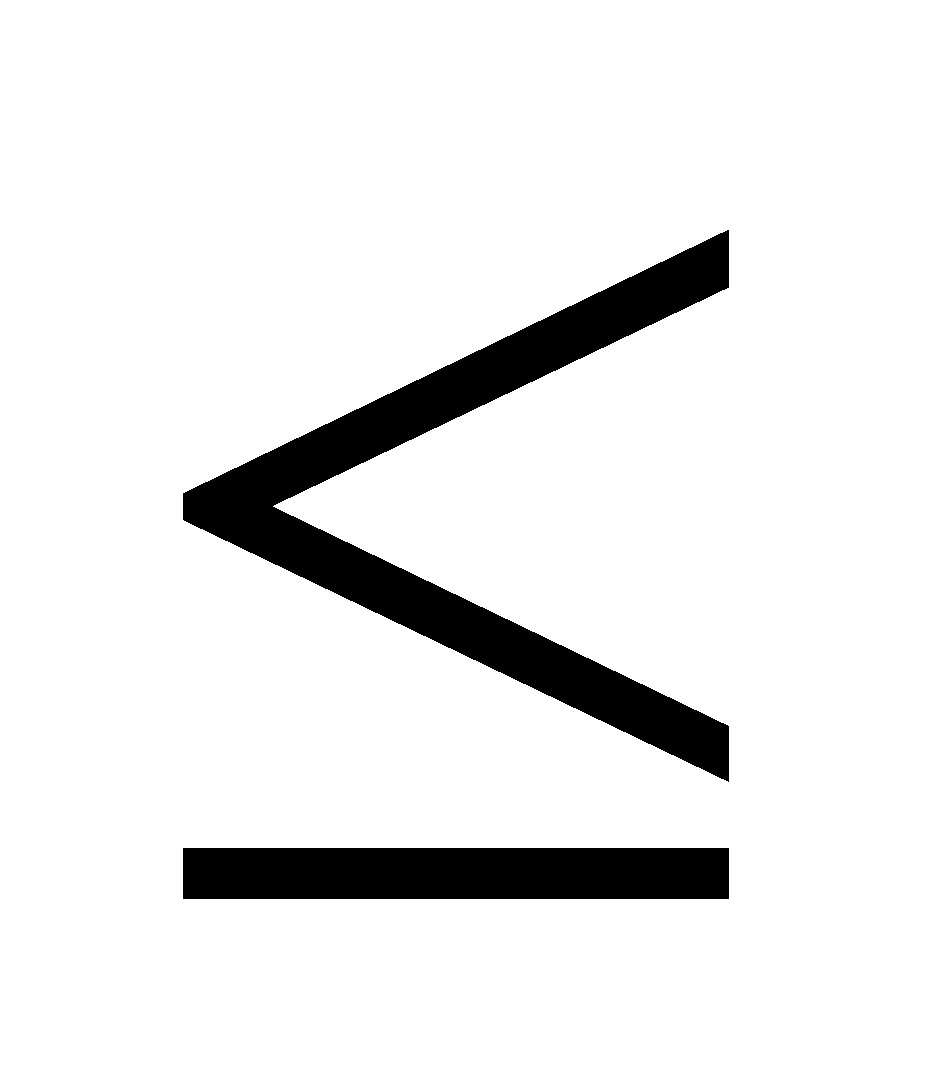
Định lí: với đa số số thực a với b ta có:
|a + b|
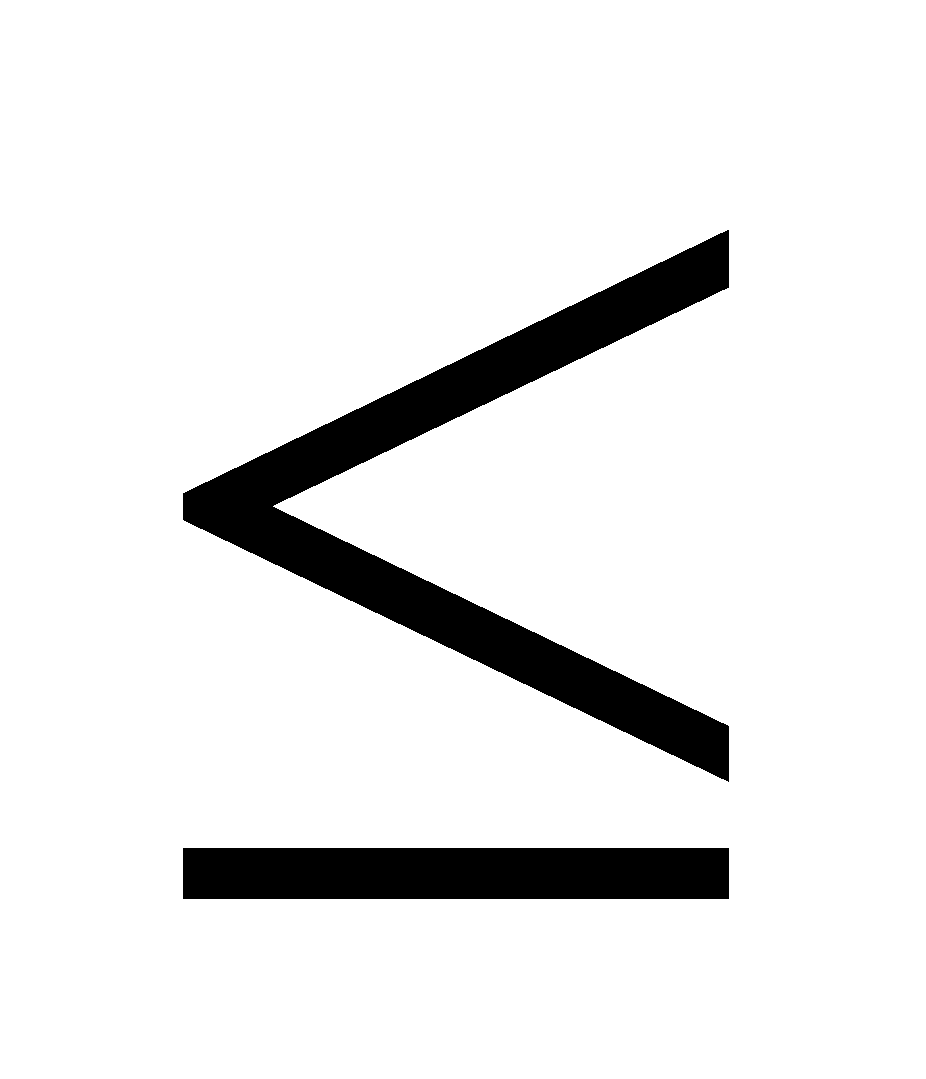
|a – b|
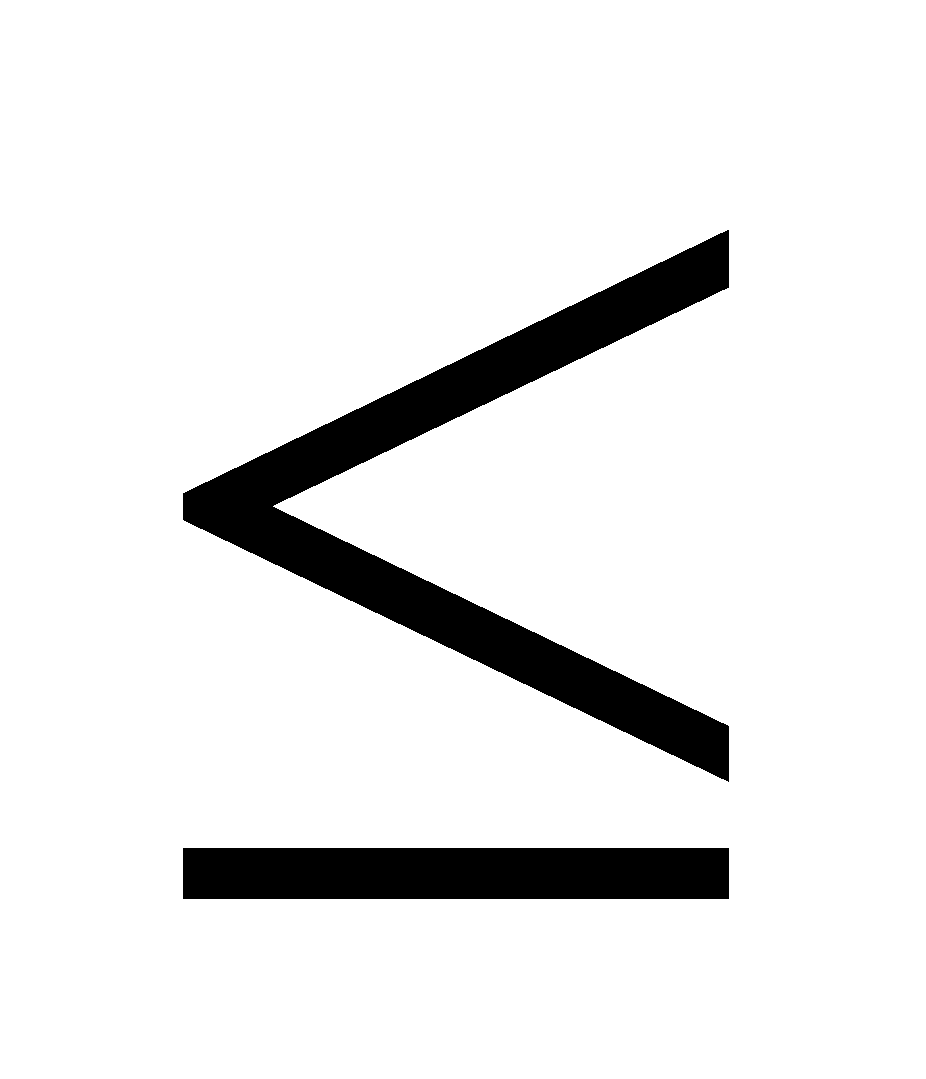
|a + b| = |a| + |b| khi còn chỉ khi a.b
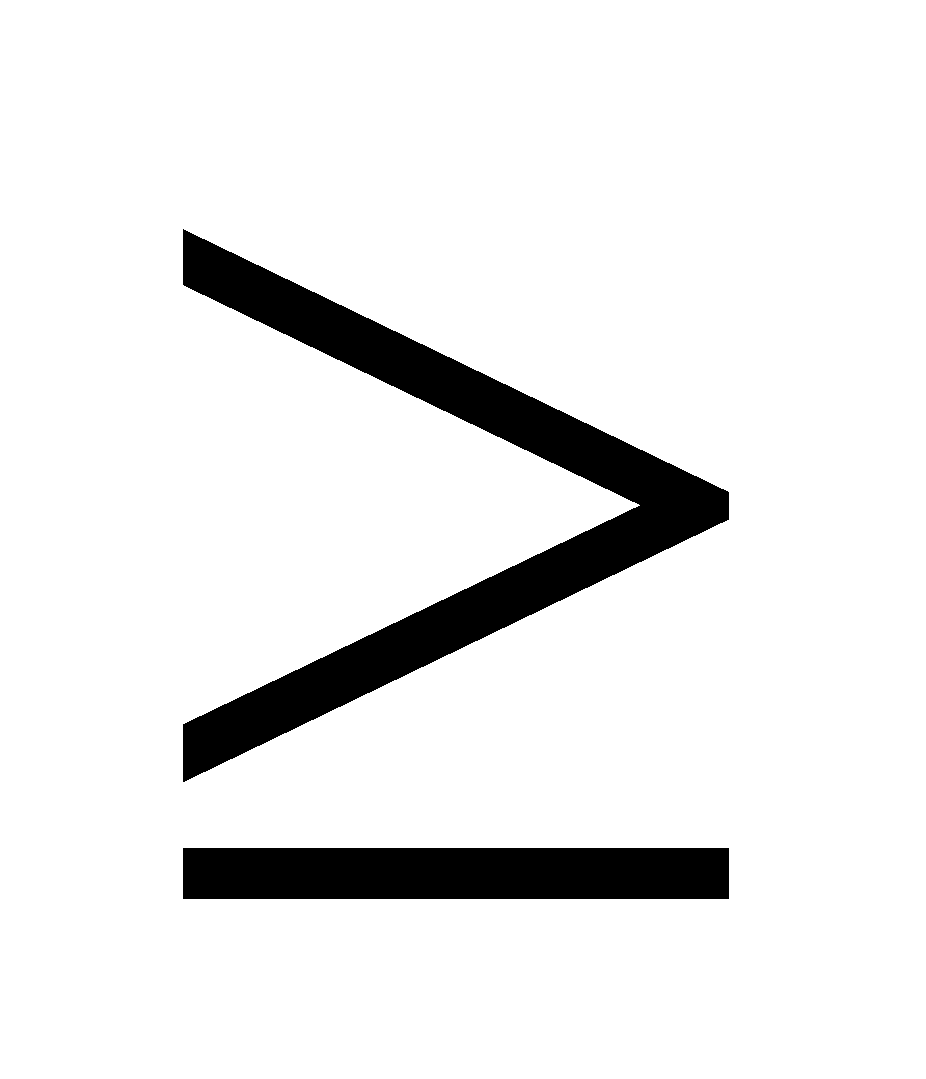
|a – b| = |a| + |b| khi và chỉ còn khi a.b
2. Các công thức về phương trình bậc hai: 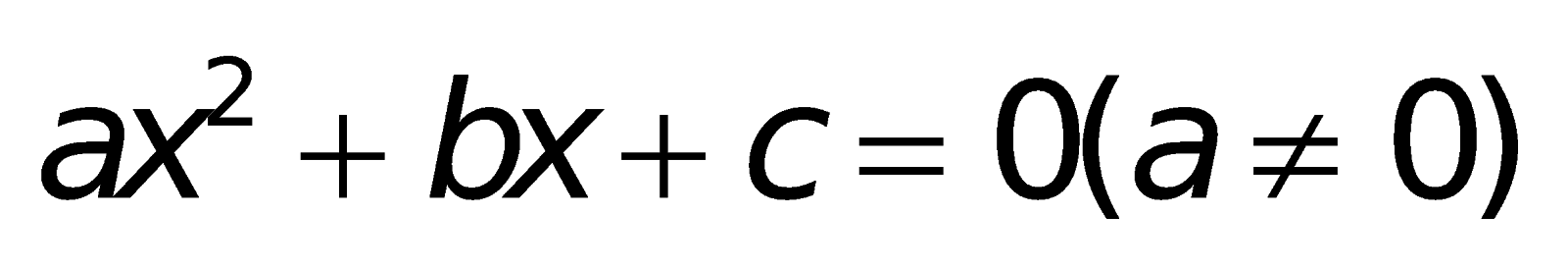
a. Công thức nghiệm của phương trình bậc hai: 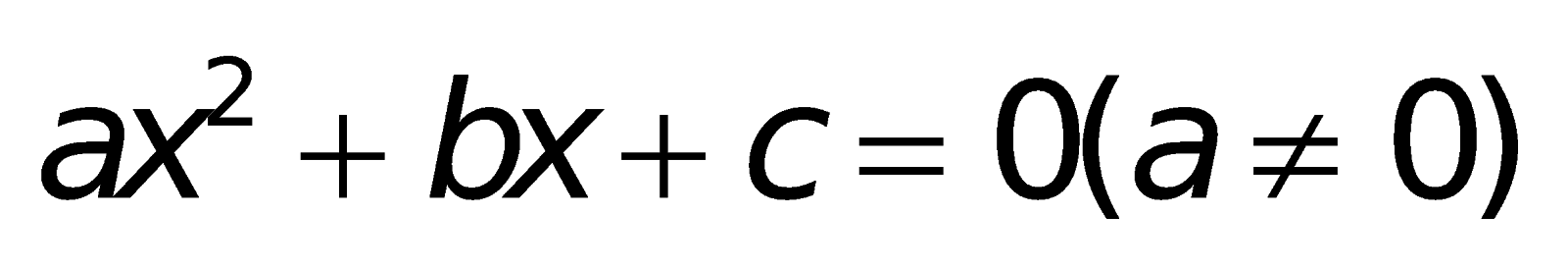
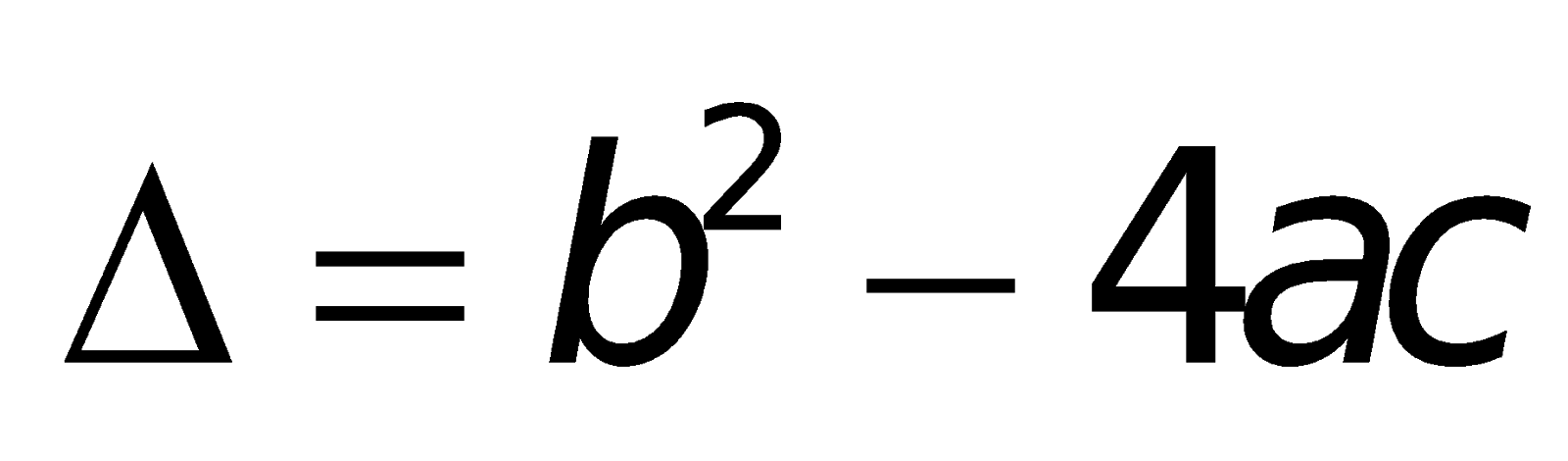
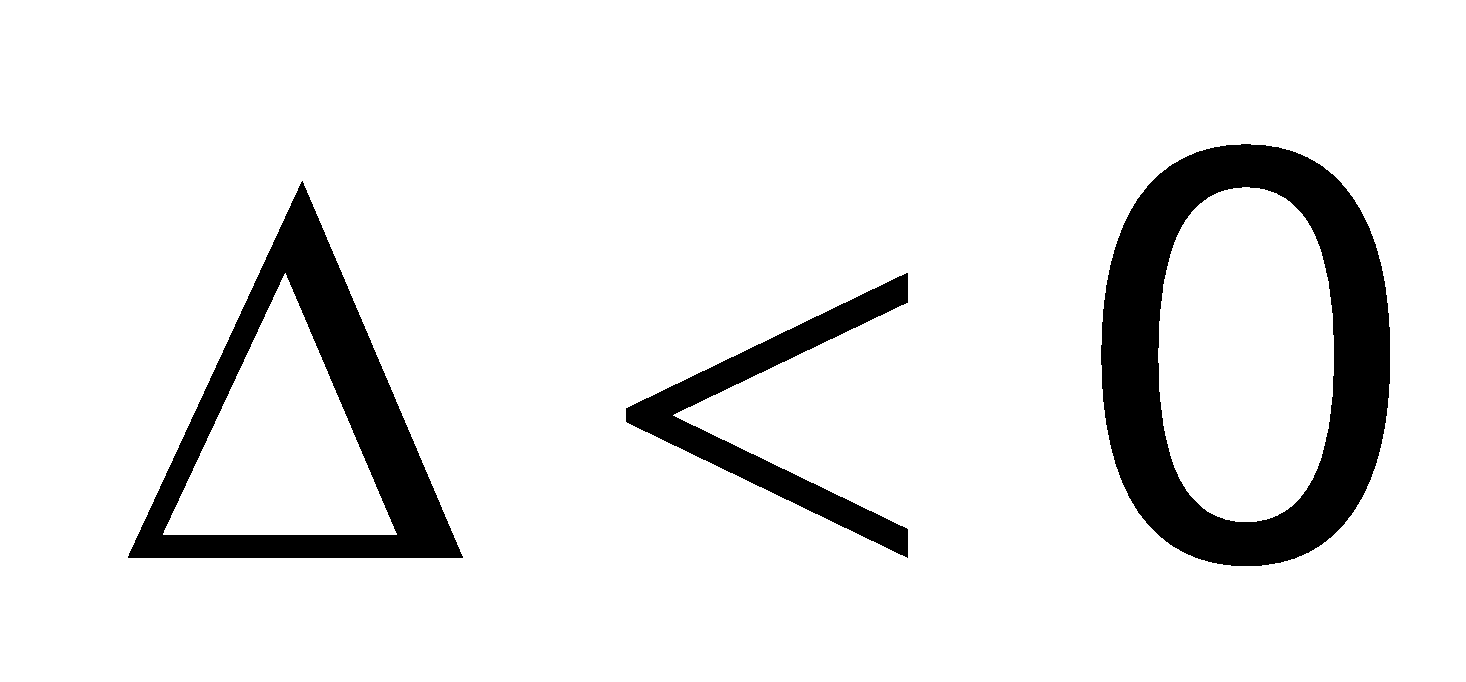
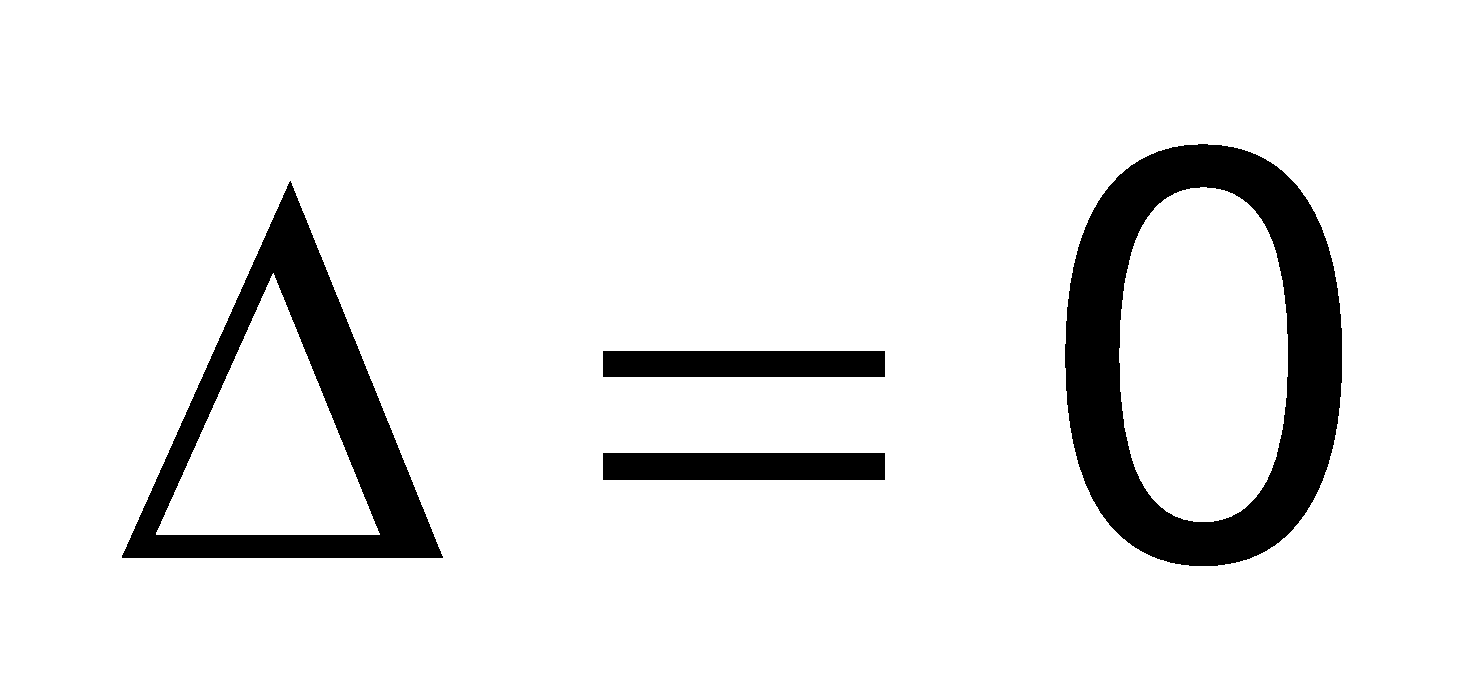
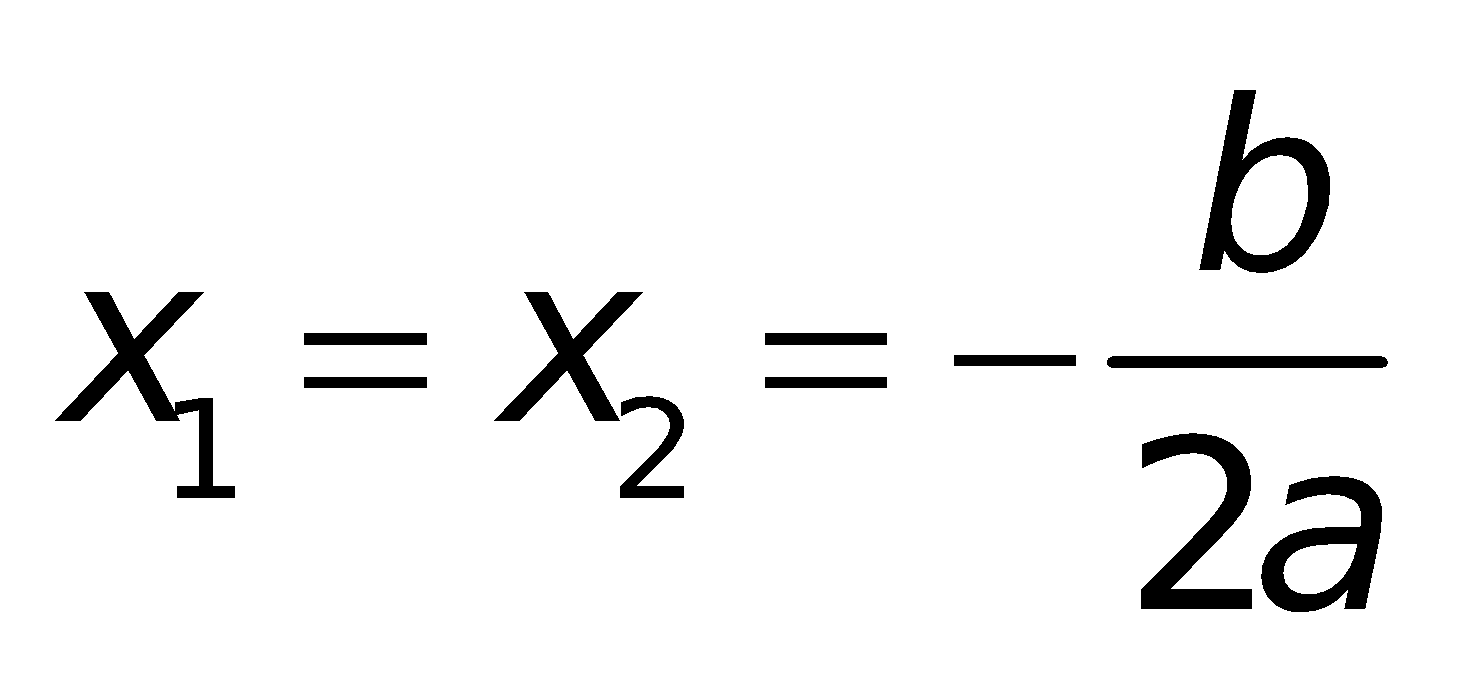
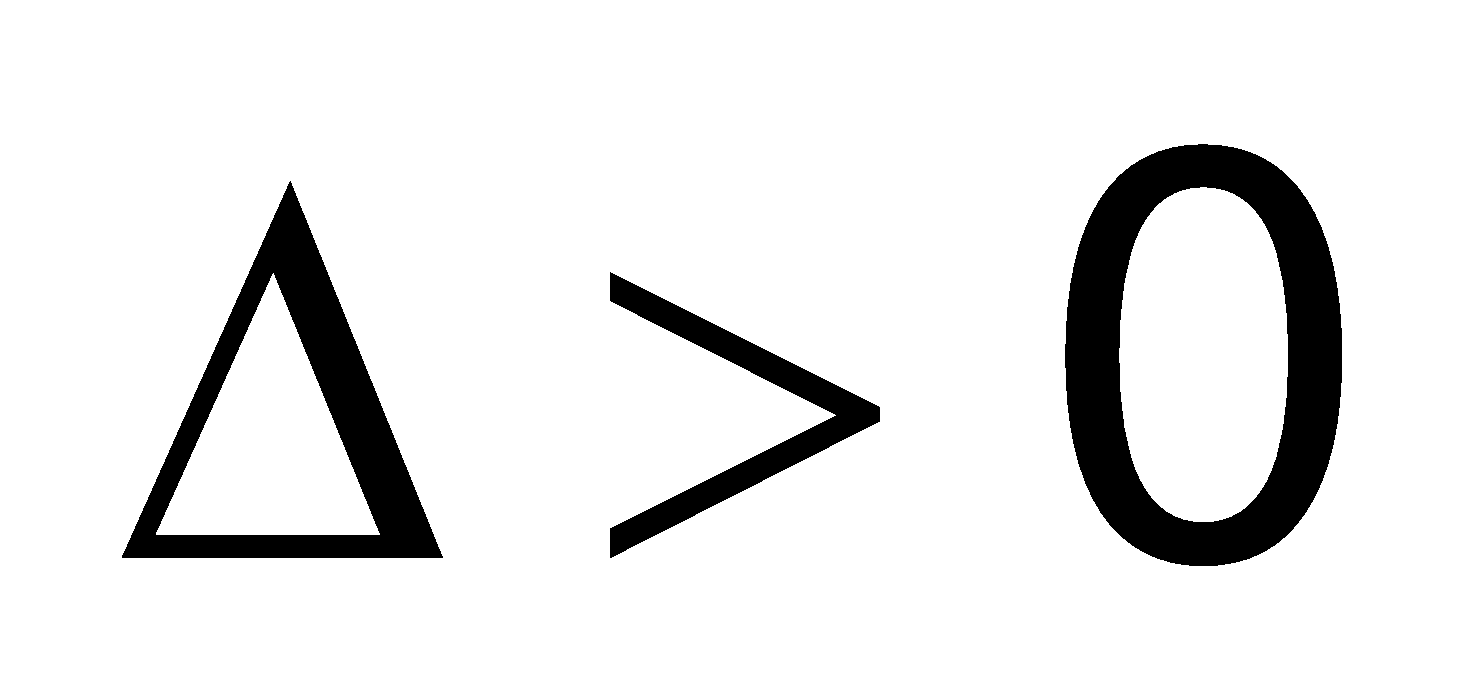
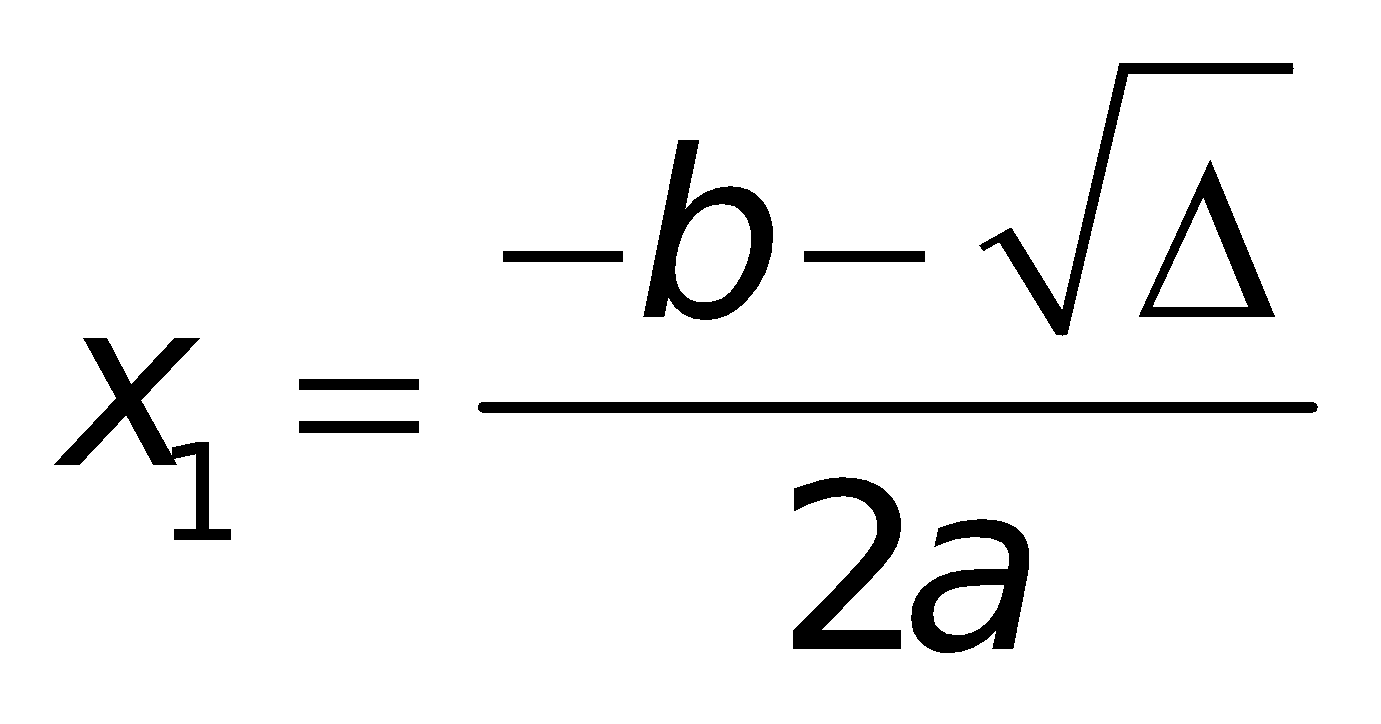

Nếu “b chẵn” (ví dụ
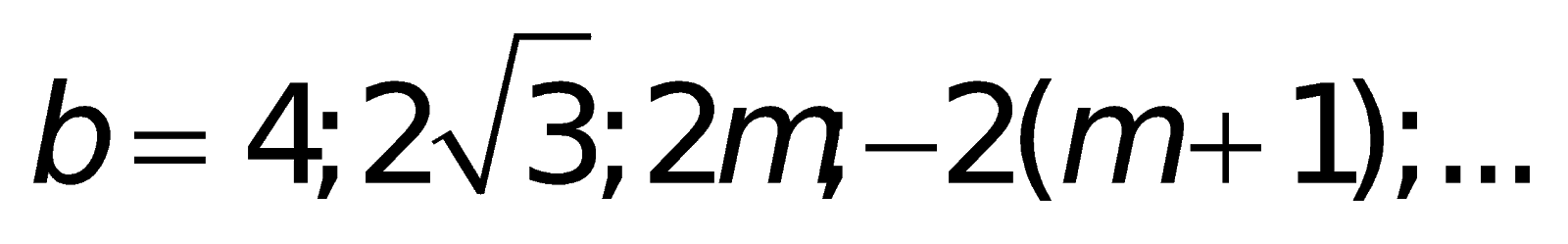
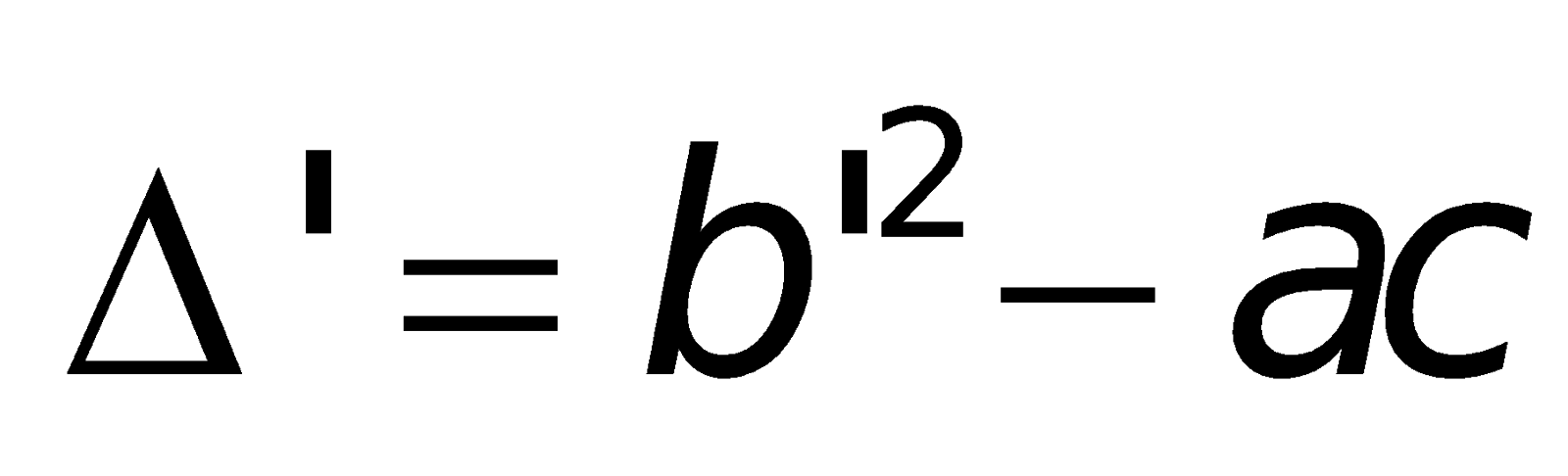
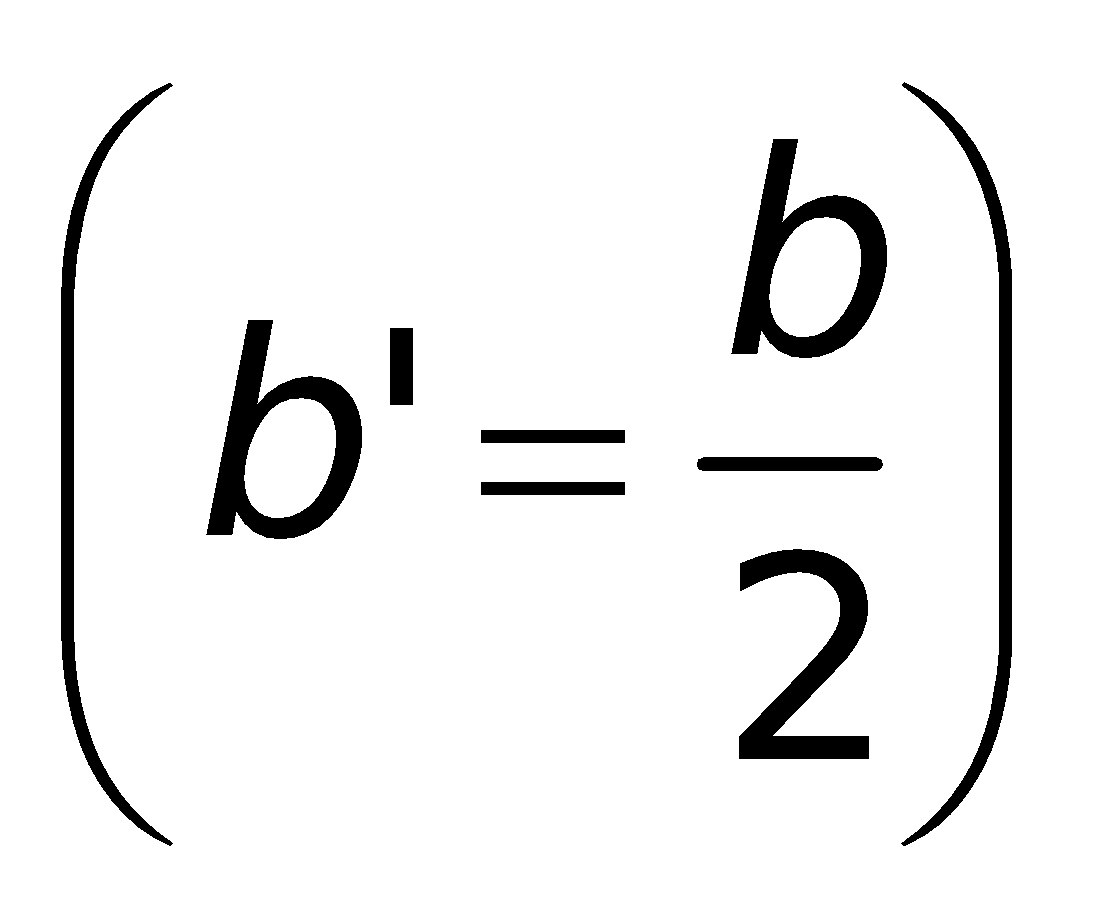
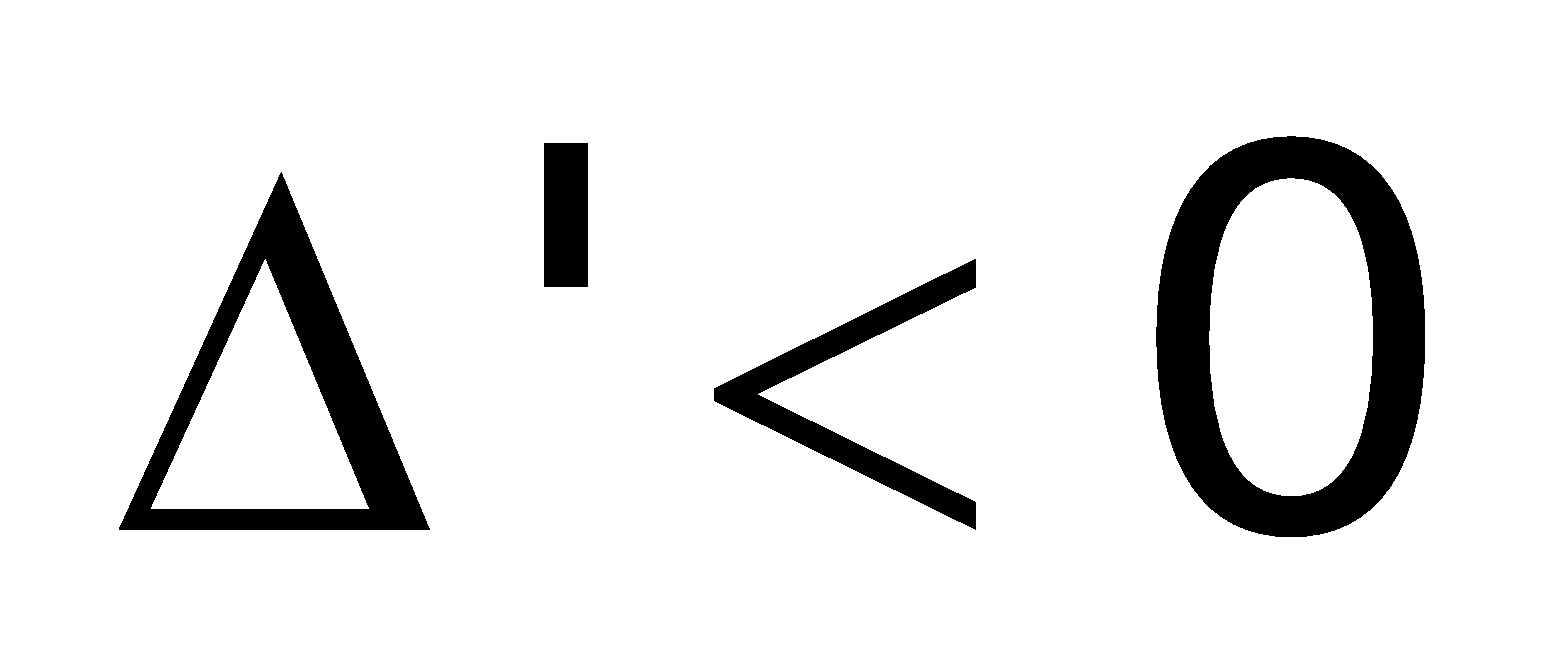
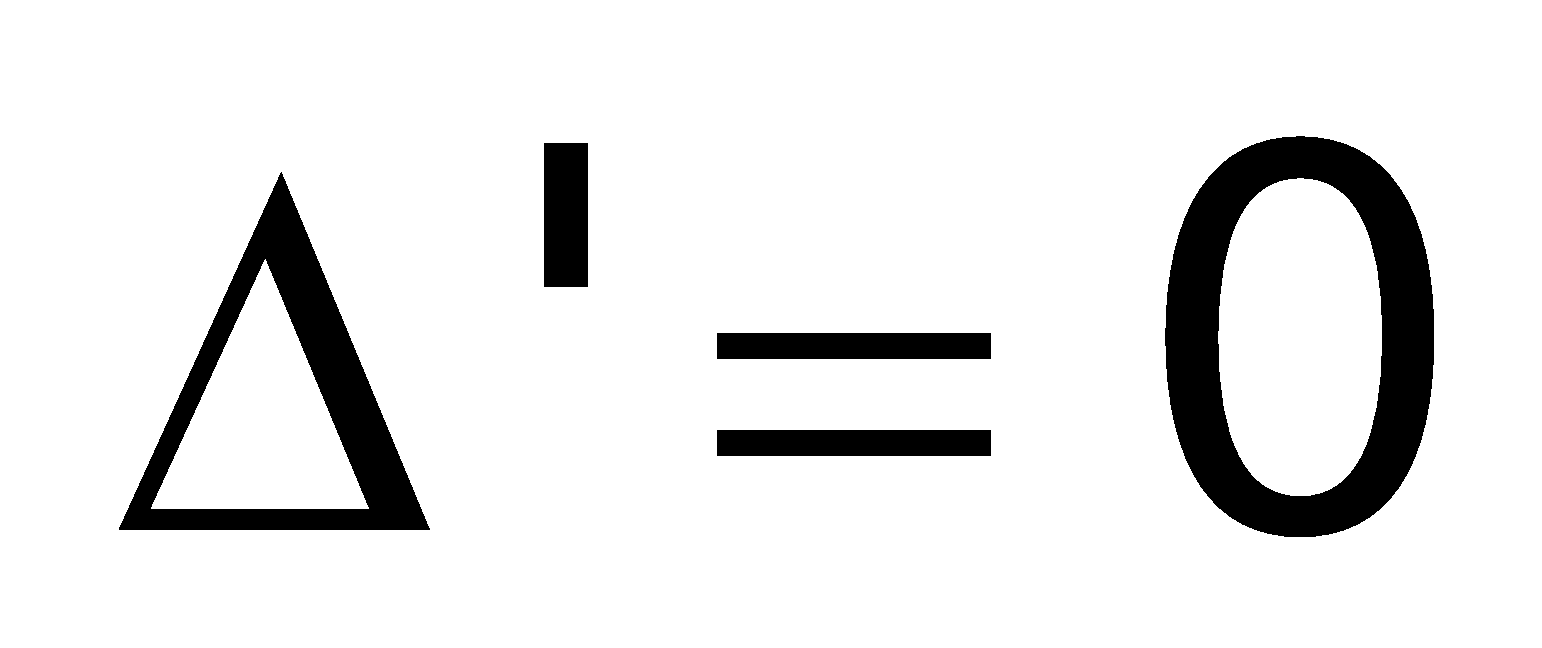
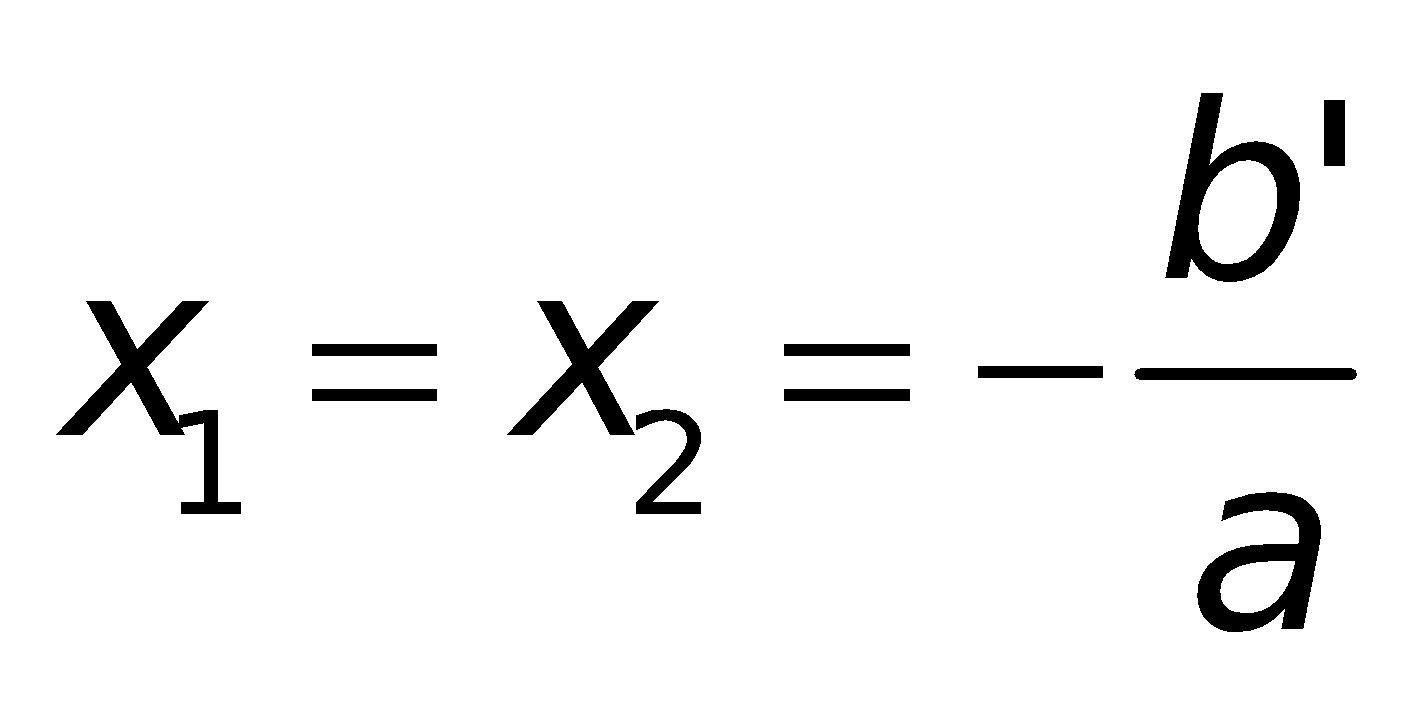
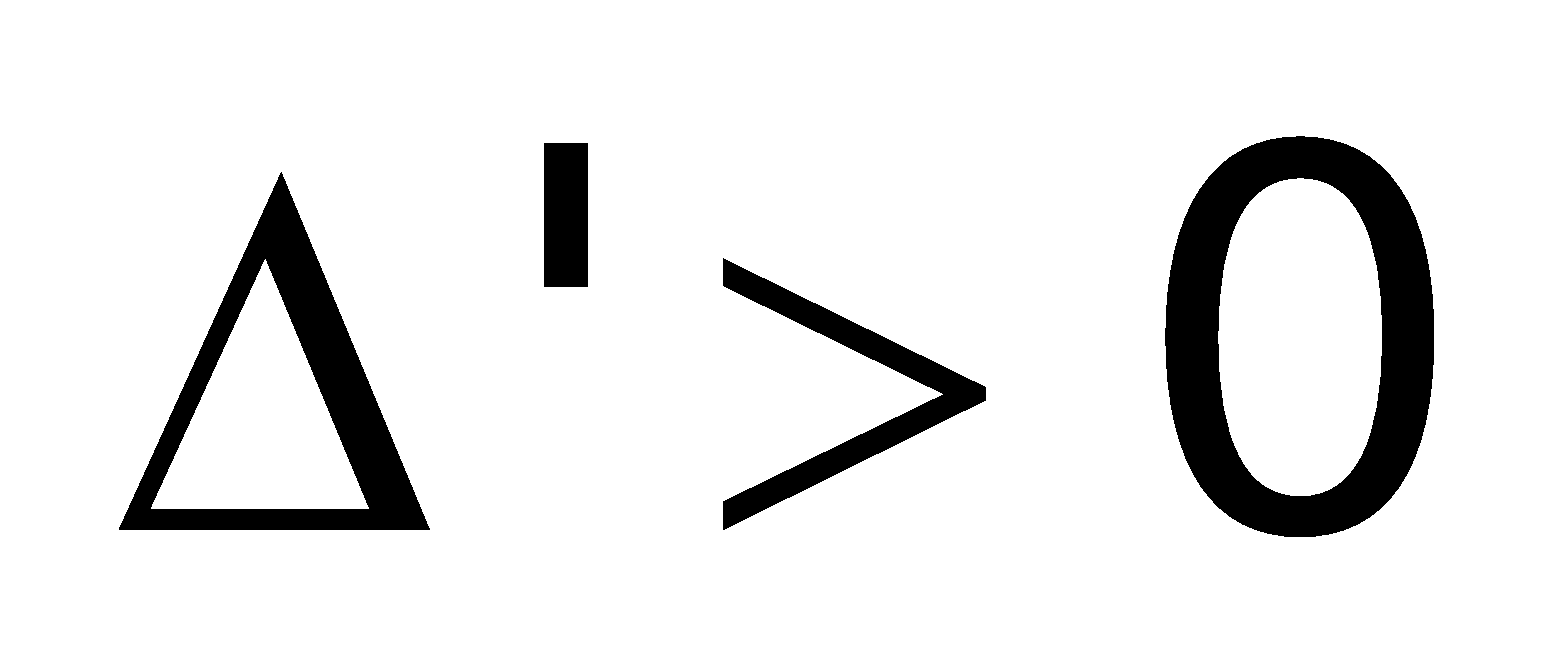
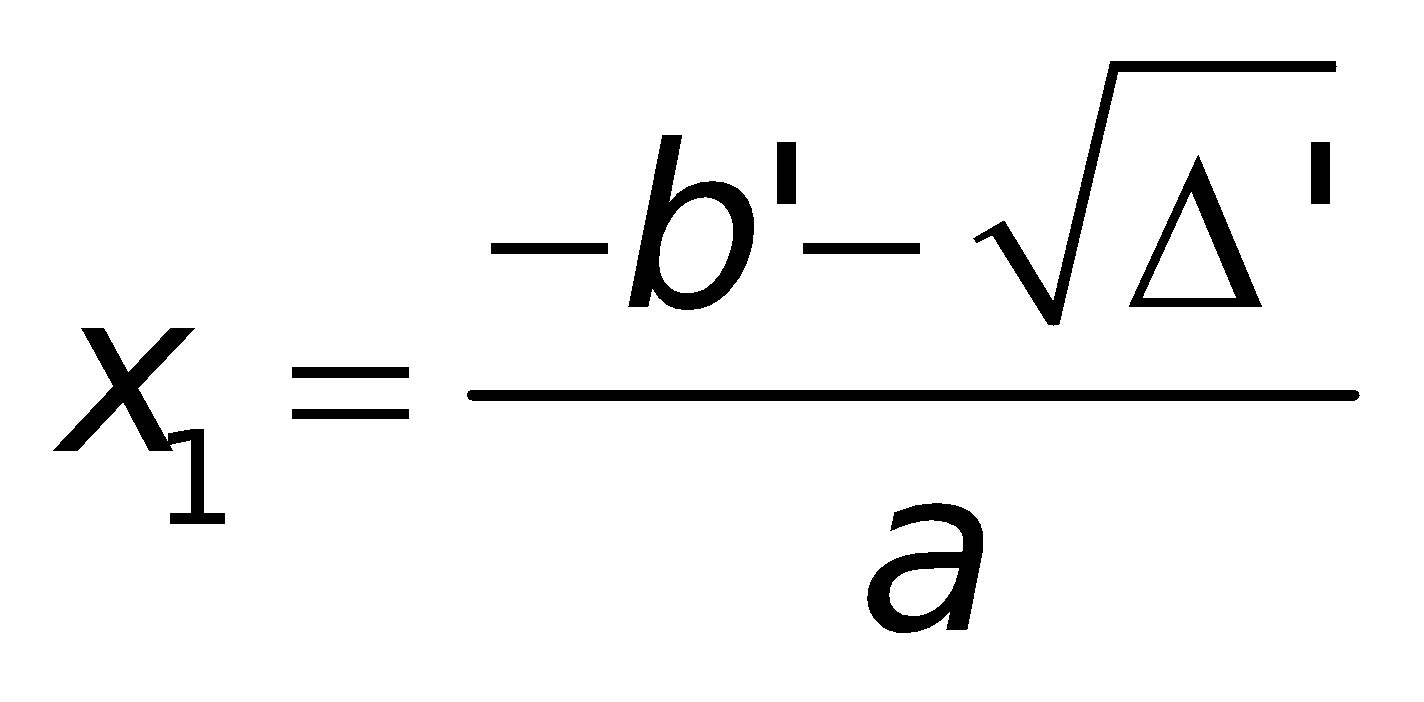
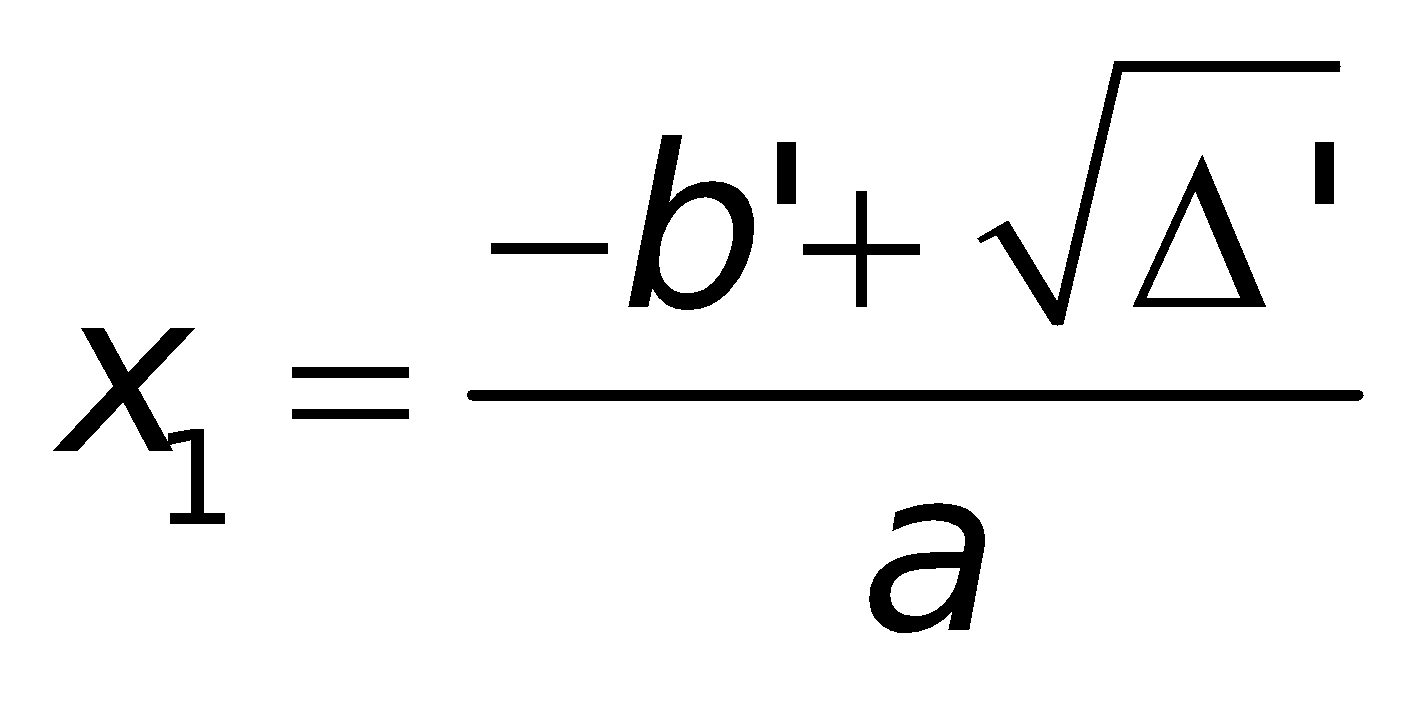
Chú ý:
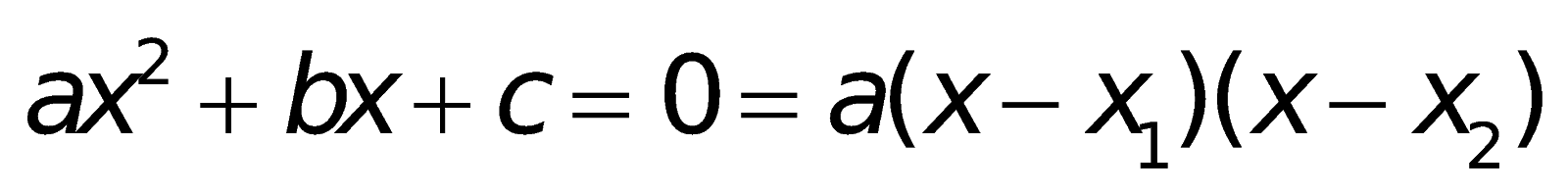
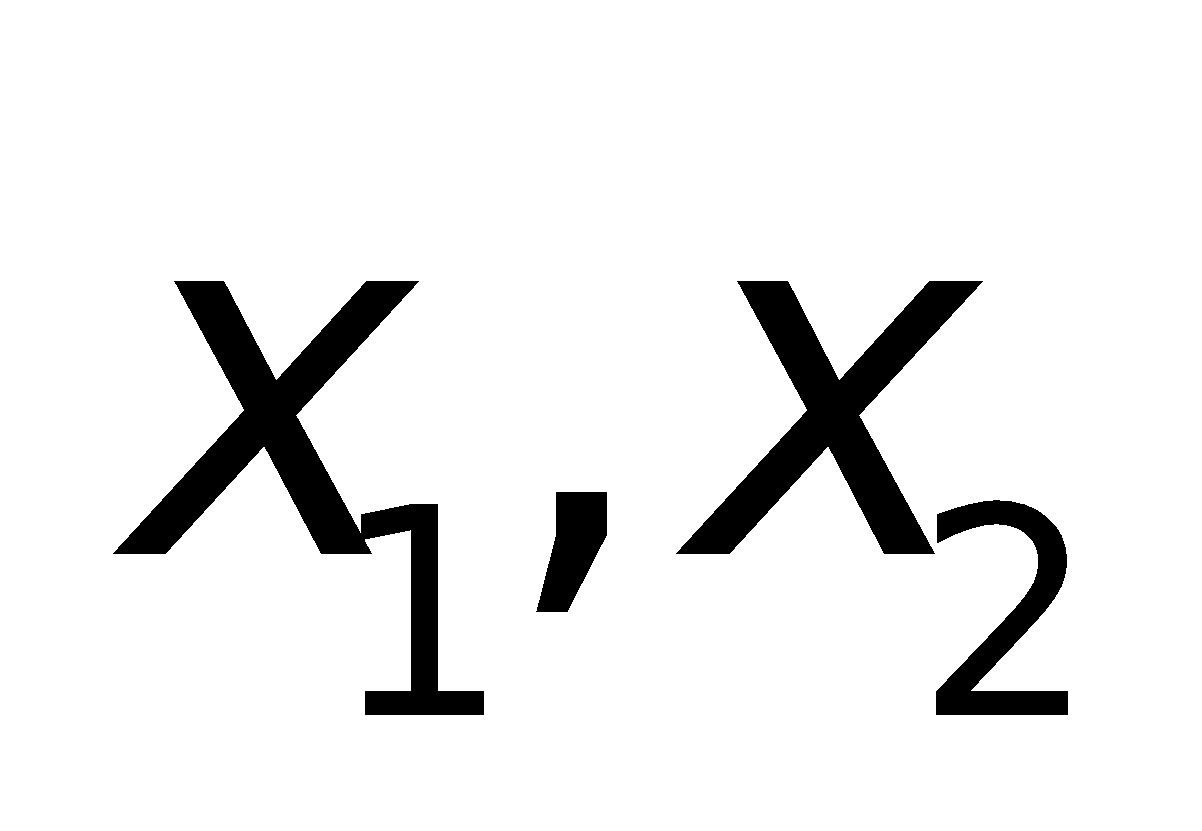
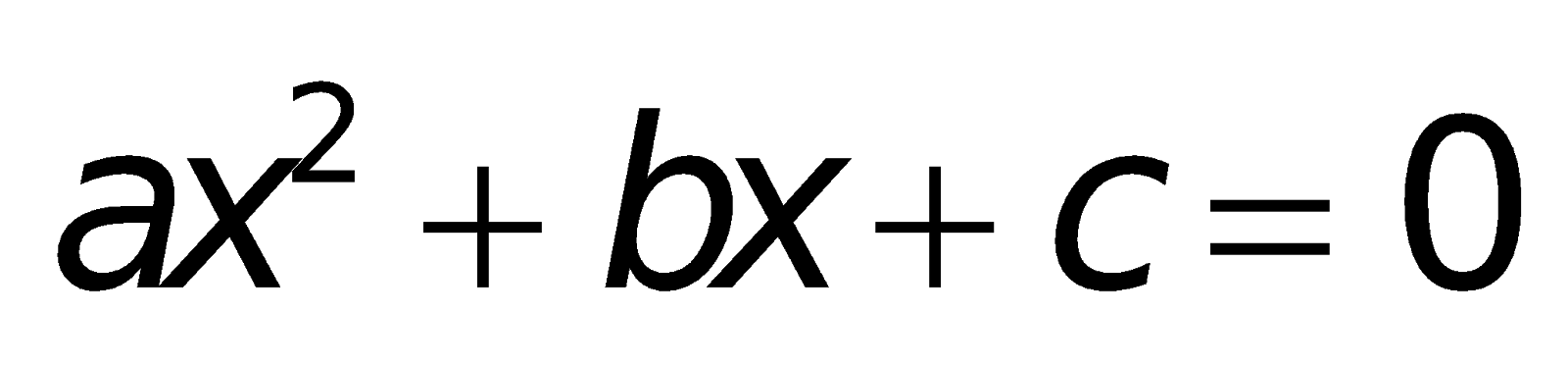
Nếu phương trình bậc 2
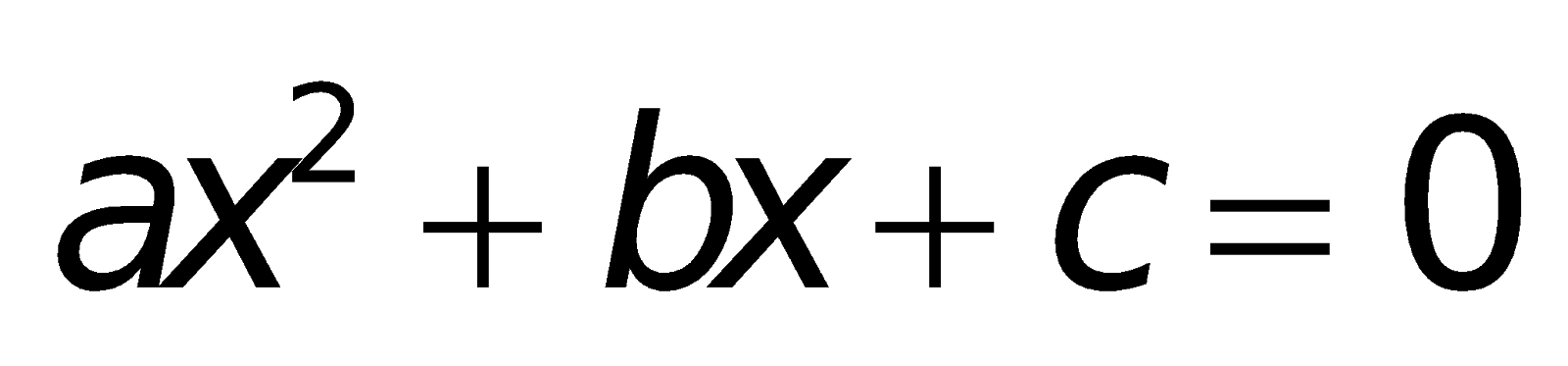
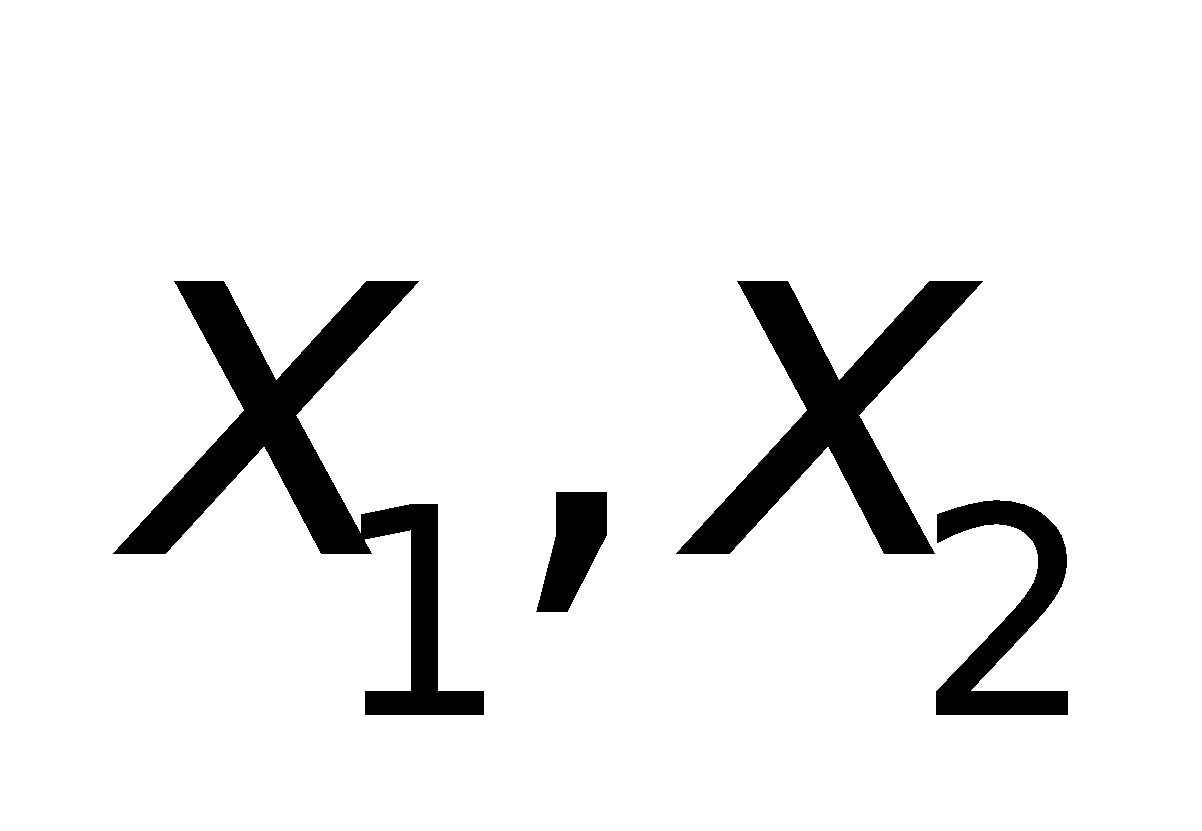
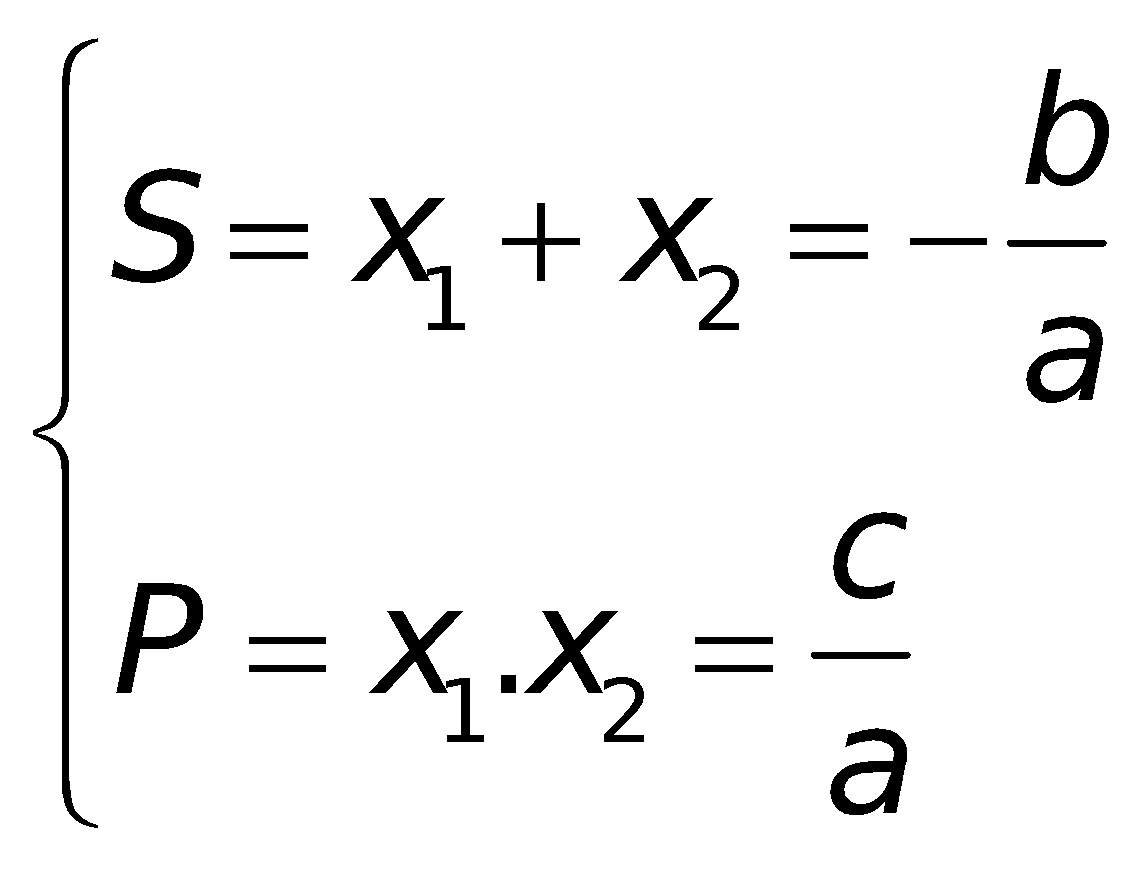
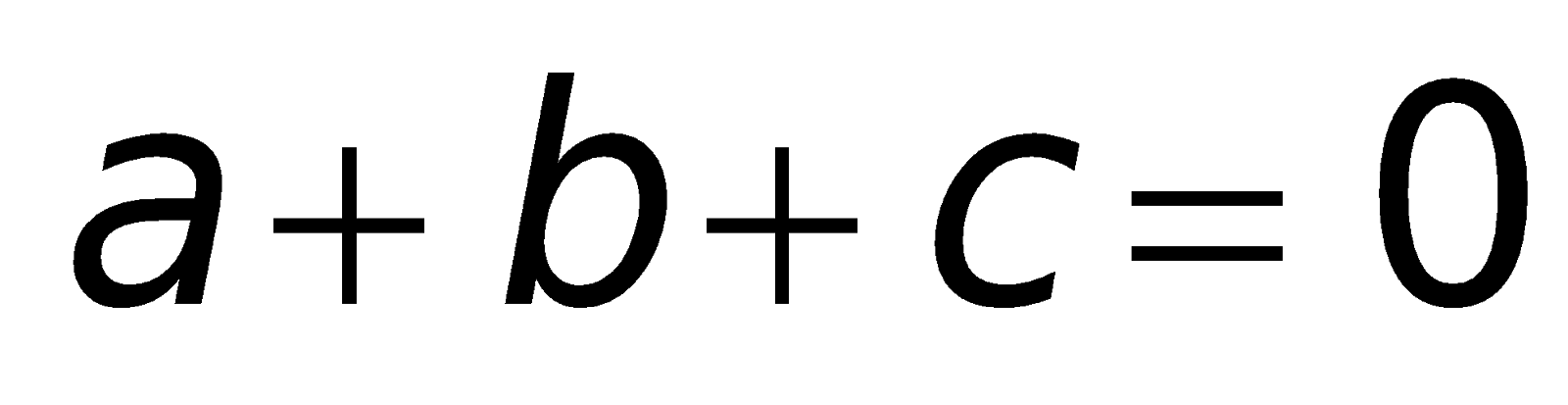
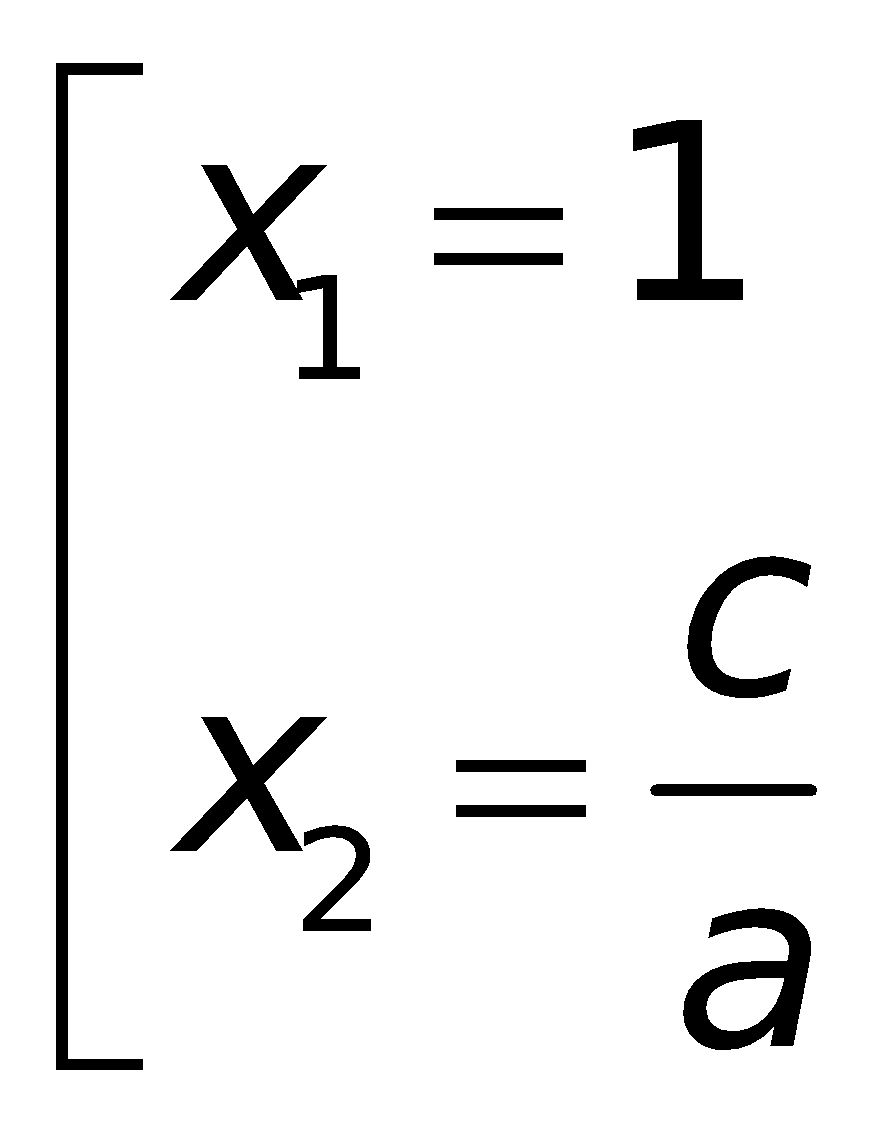
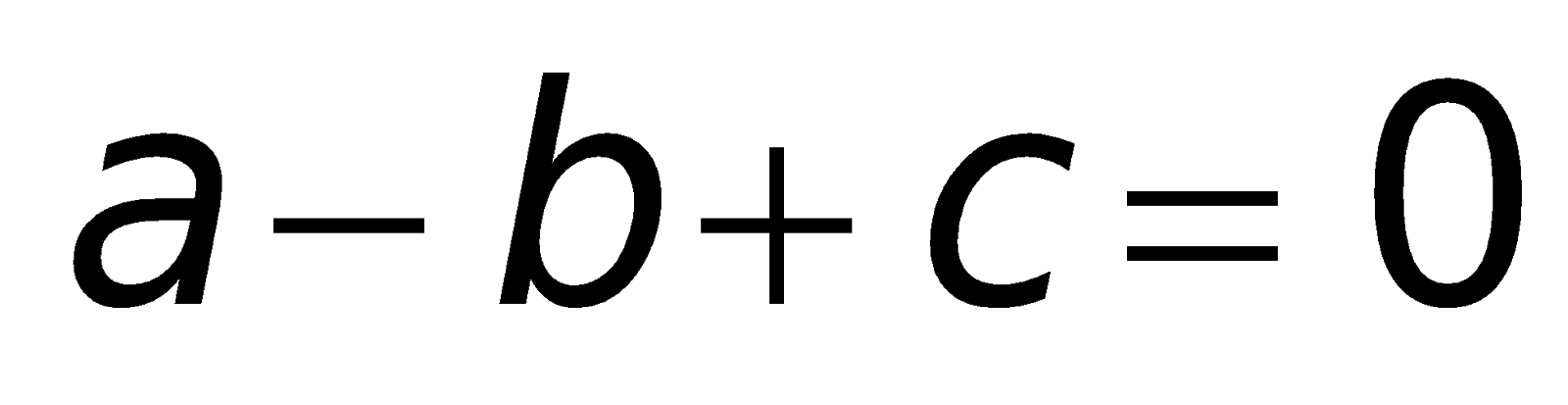
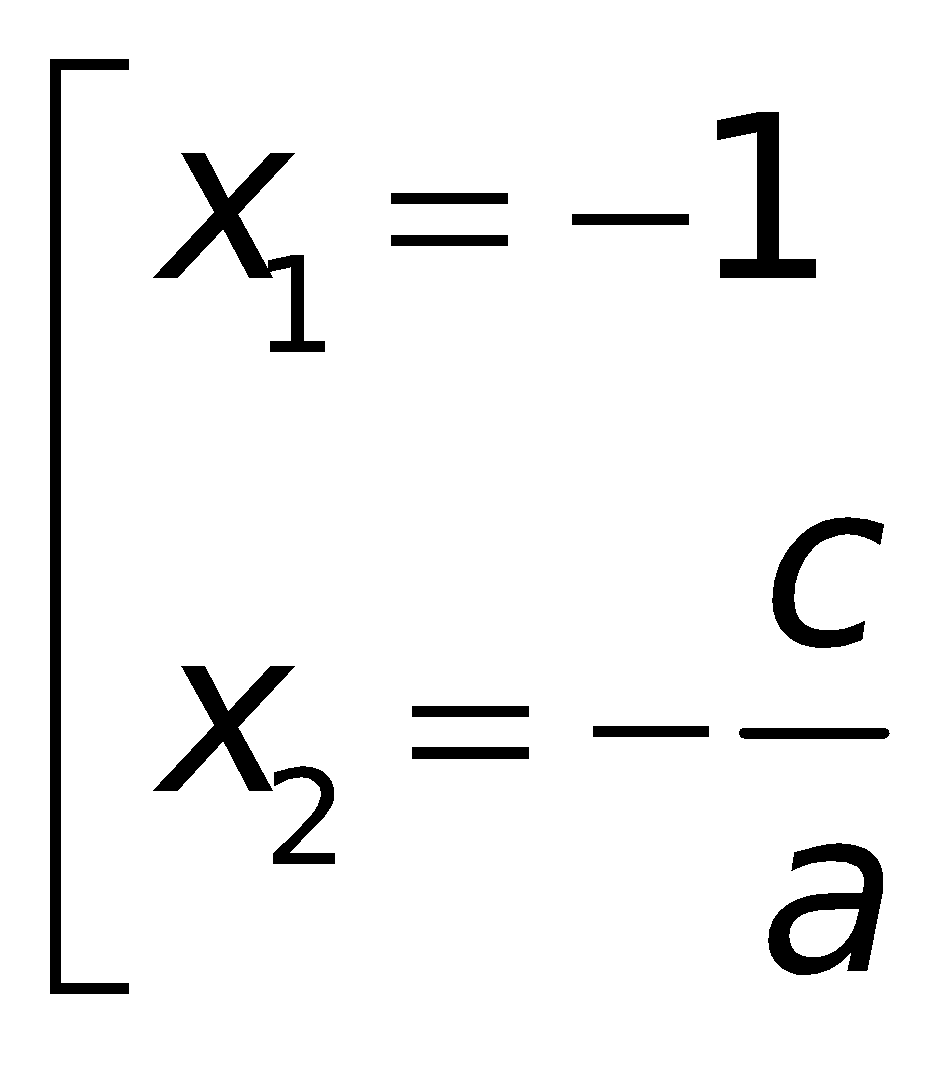
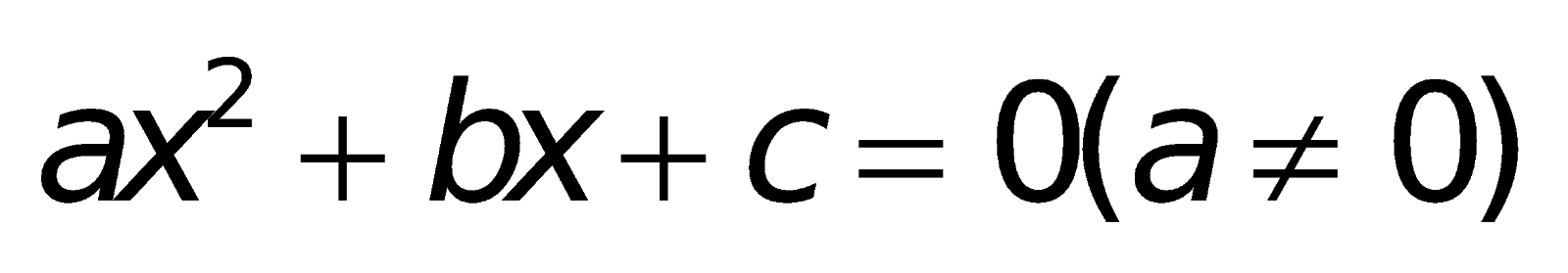
- Phương trình gồm 2 nghiệm trái dấu:
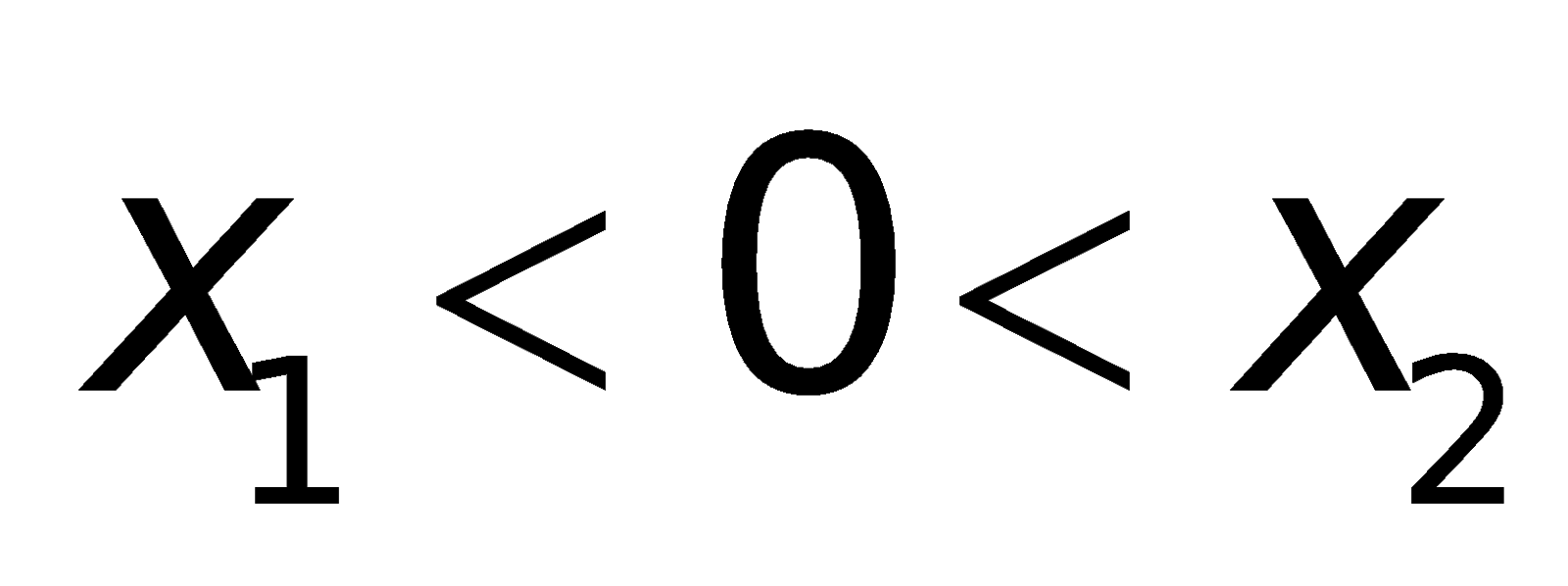
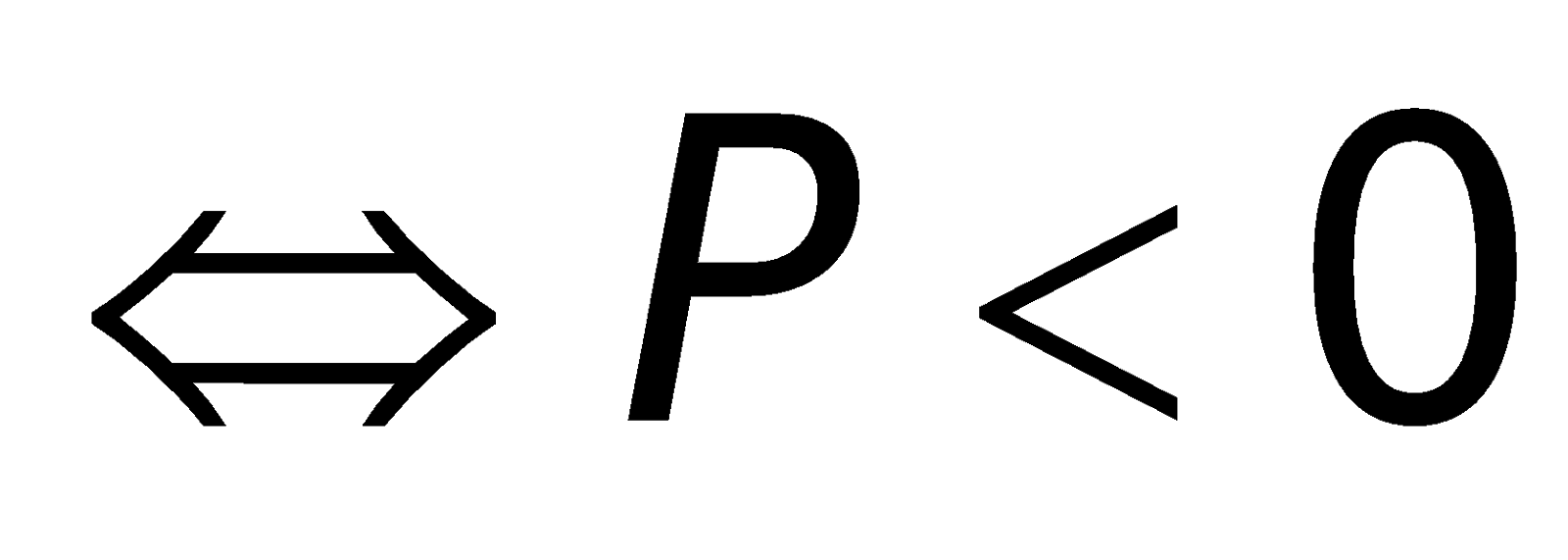
- Phương trình gồm 2 nghiệm dương phân biệt:
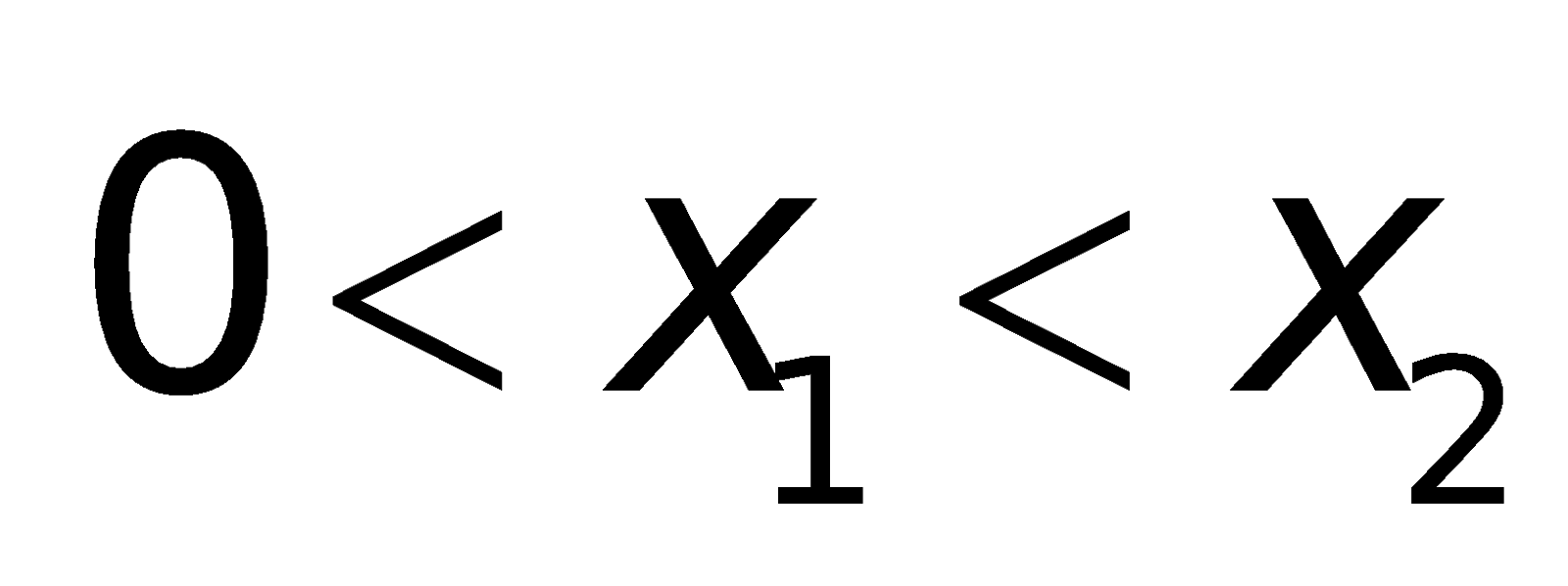
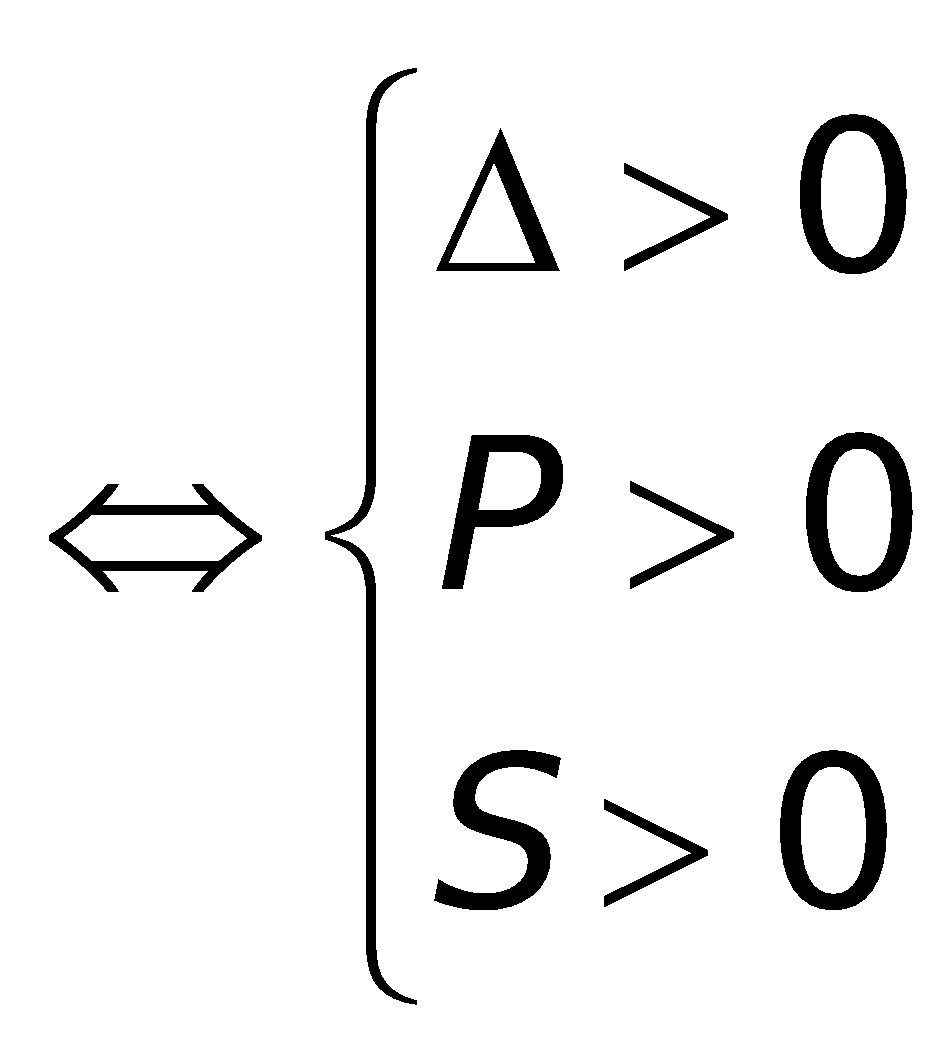
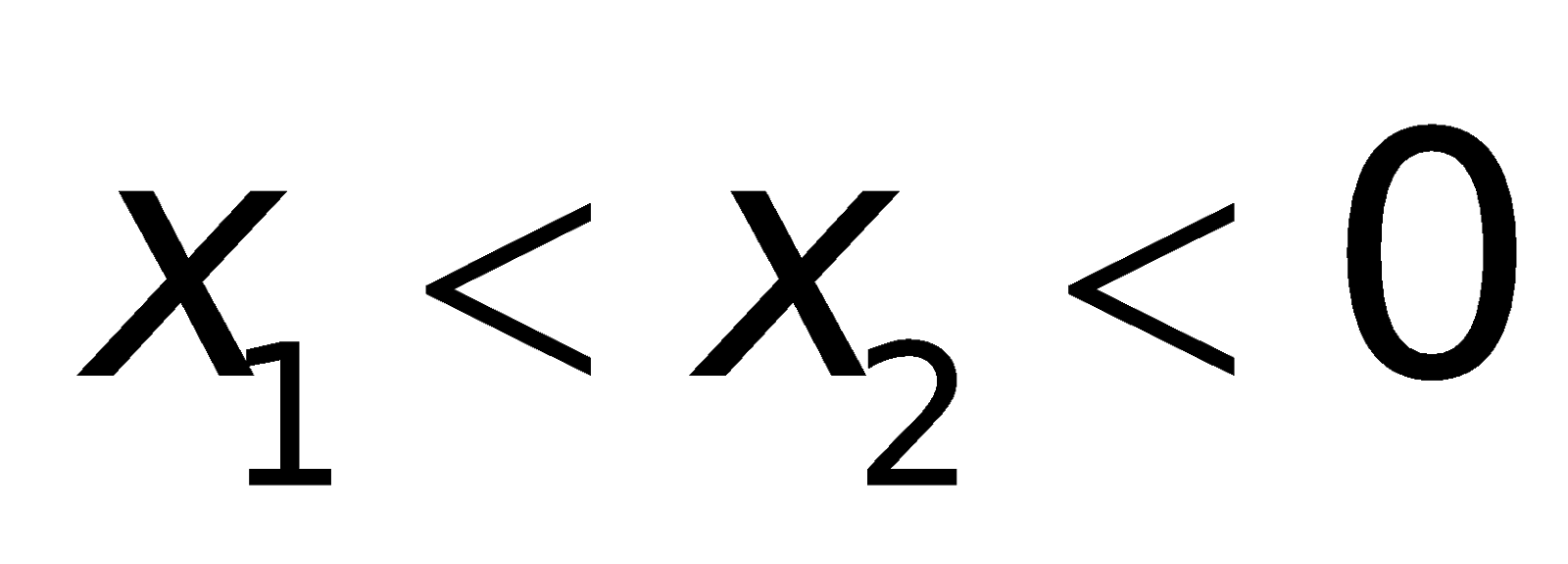
3. Các công thức về dấu của nhiều thức:
a. Dấu của nhị thức bậc nhất:
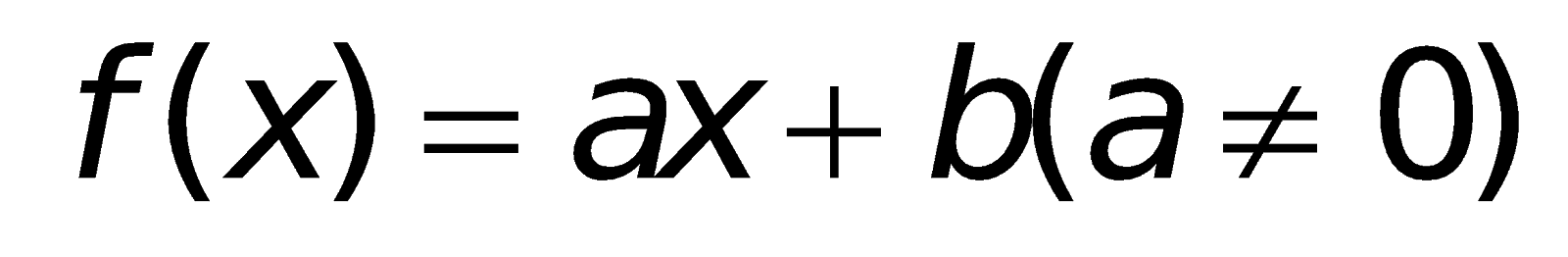
 |  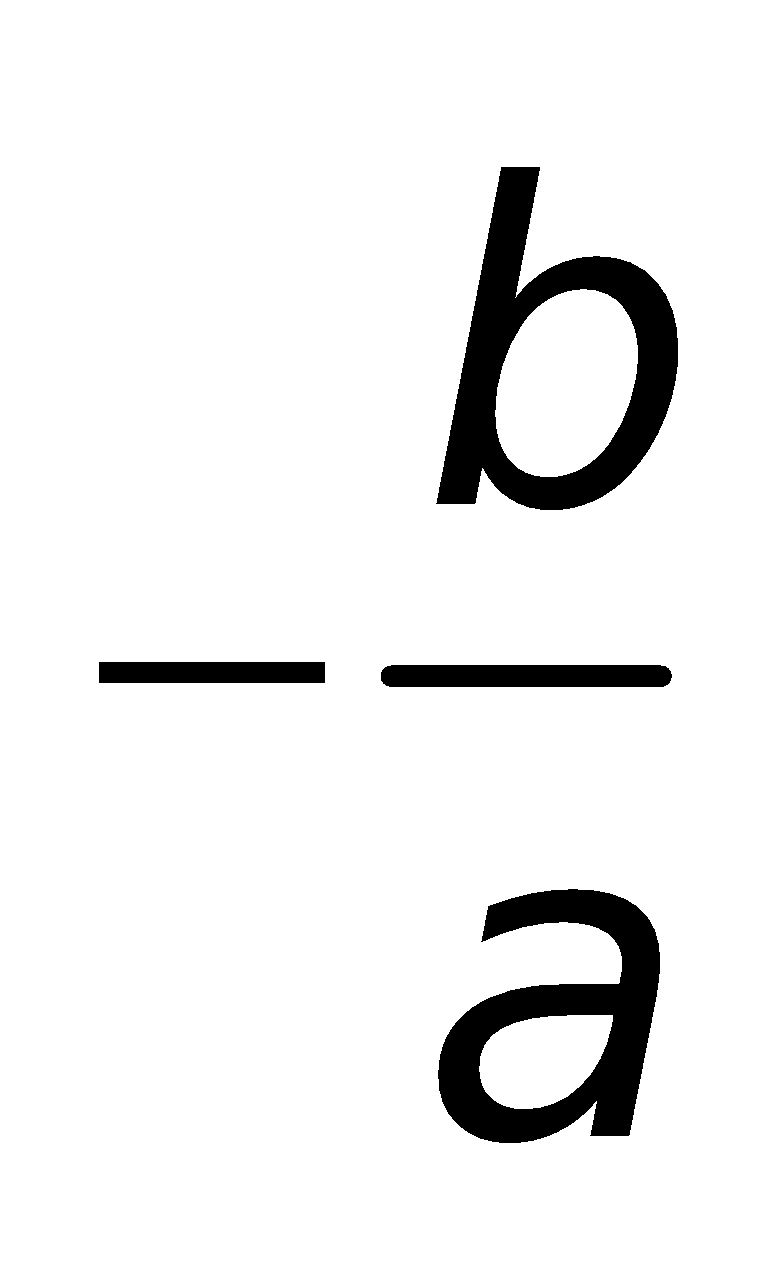  |
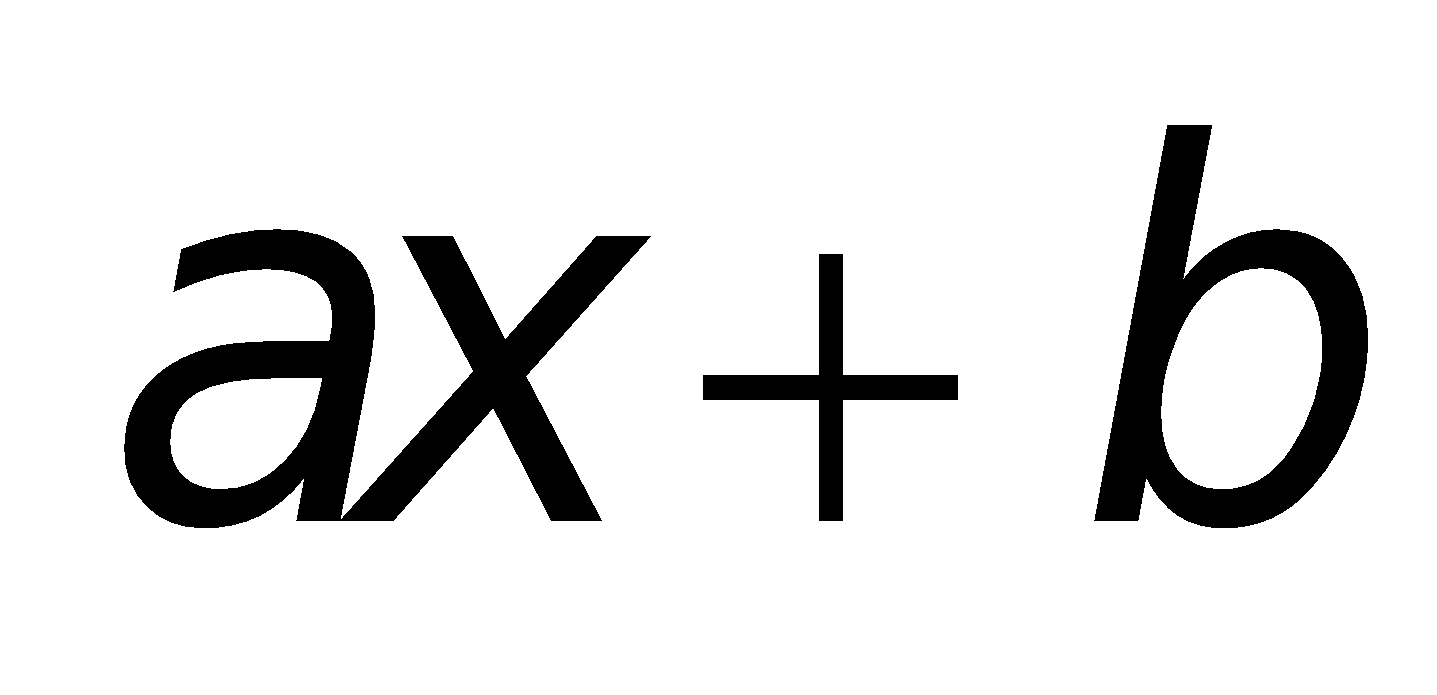 | trái dấu a 0 thuộc dấu a |
“Phải cùng, trái trái”
b. Lốt của tam thức bậc hai:
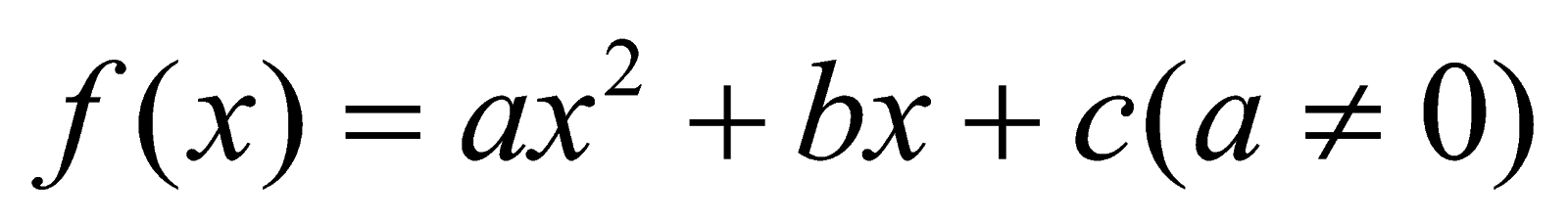
△
△=0: f(x) cùng dấu với thông số a với mọi
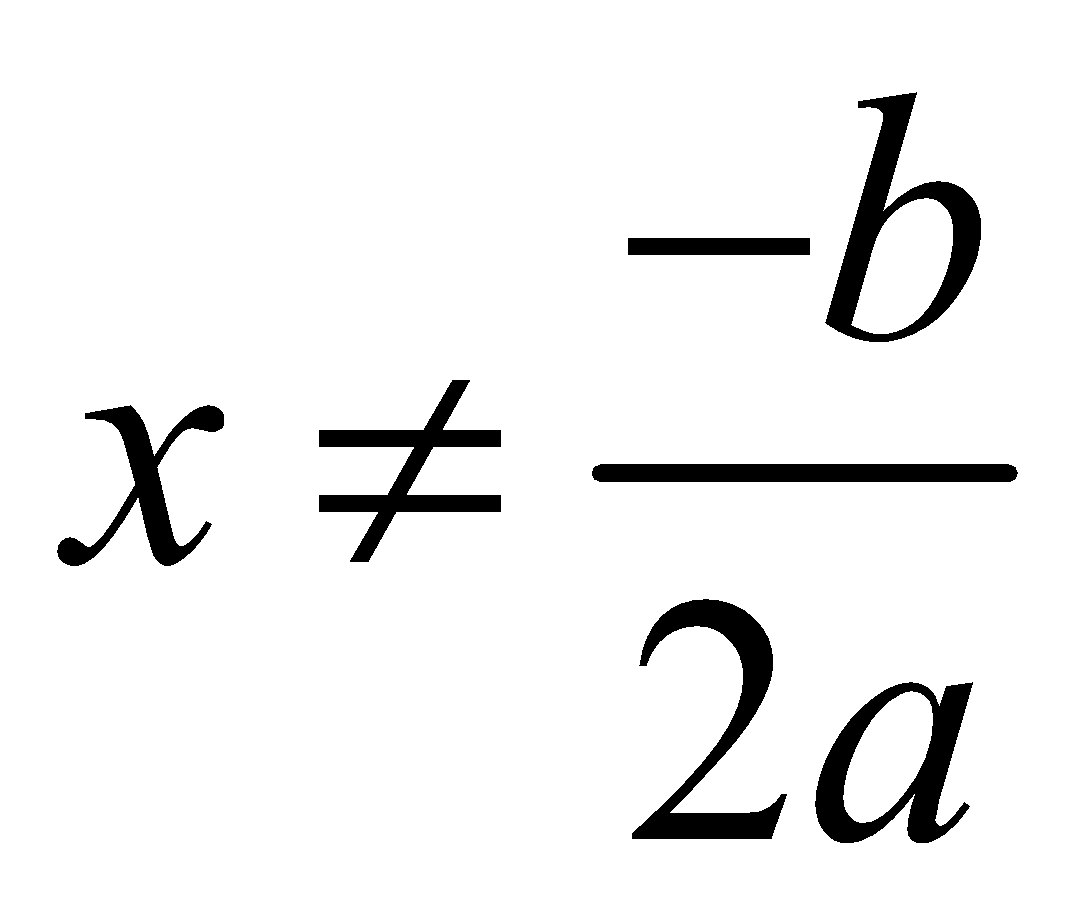
△=0: f(x) gồm 2 nghiệm x1 , x2
 | 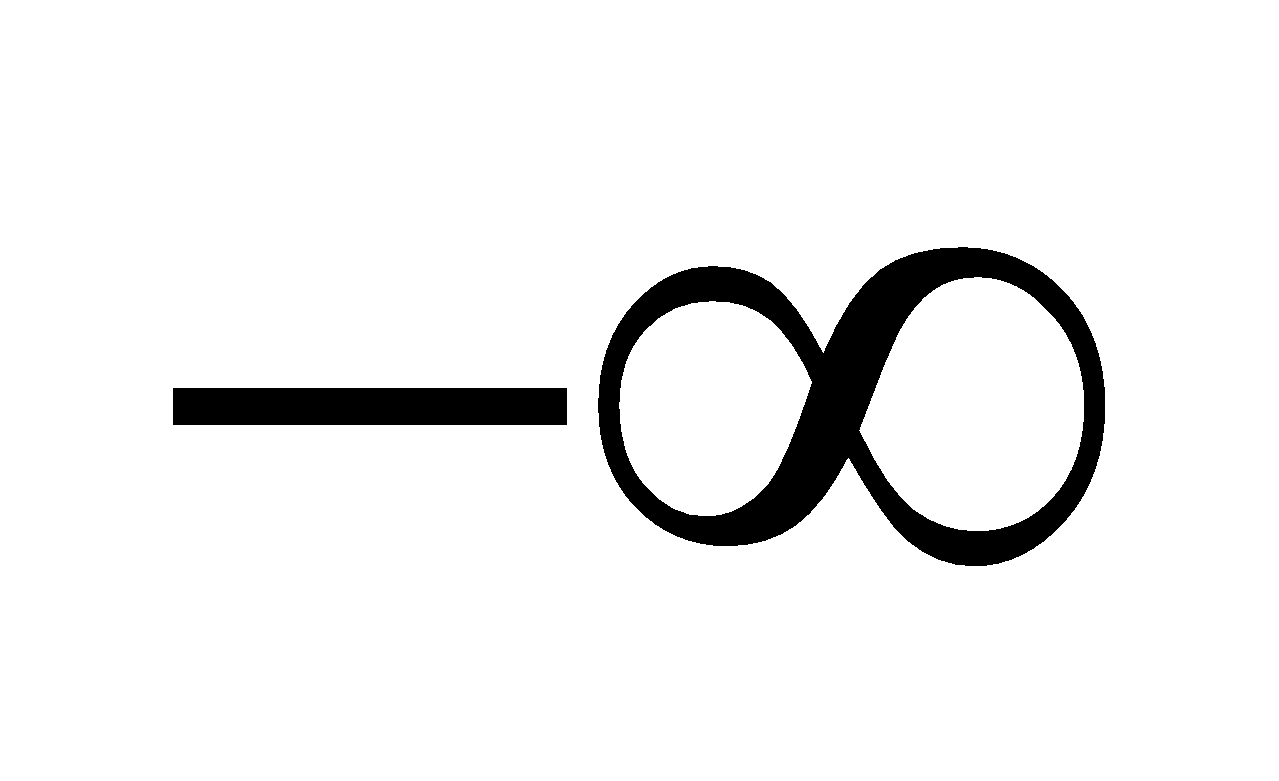 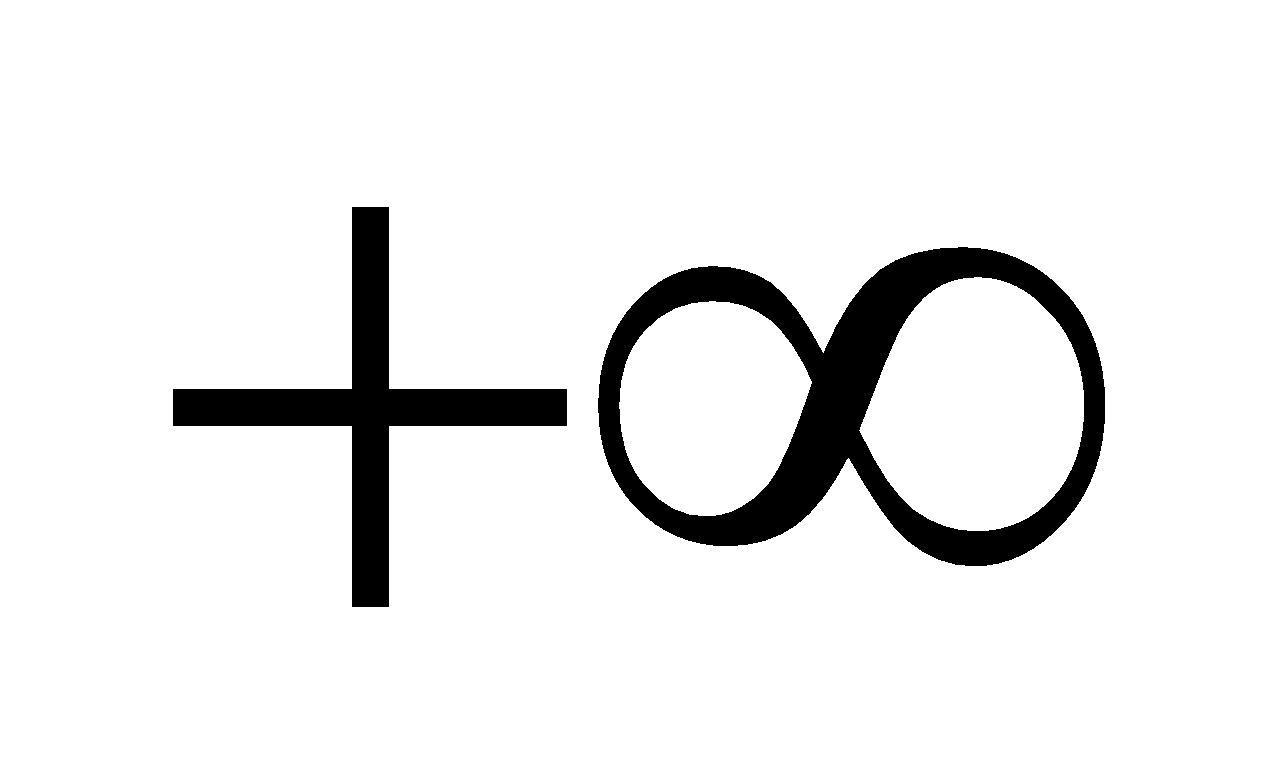 |
F(x) | cùng dấu a 0 trái vệt a 0 cùng dấu a |
c. Dấu của đa thức bậc ≥3: bước đầu từ ô bên buộc phải cùng vệt với hệ số a của số nón cao nhất, qua nghiệm đối kháng đổi dấu, qua nghiệm kép không thay đổi dấu.
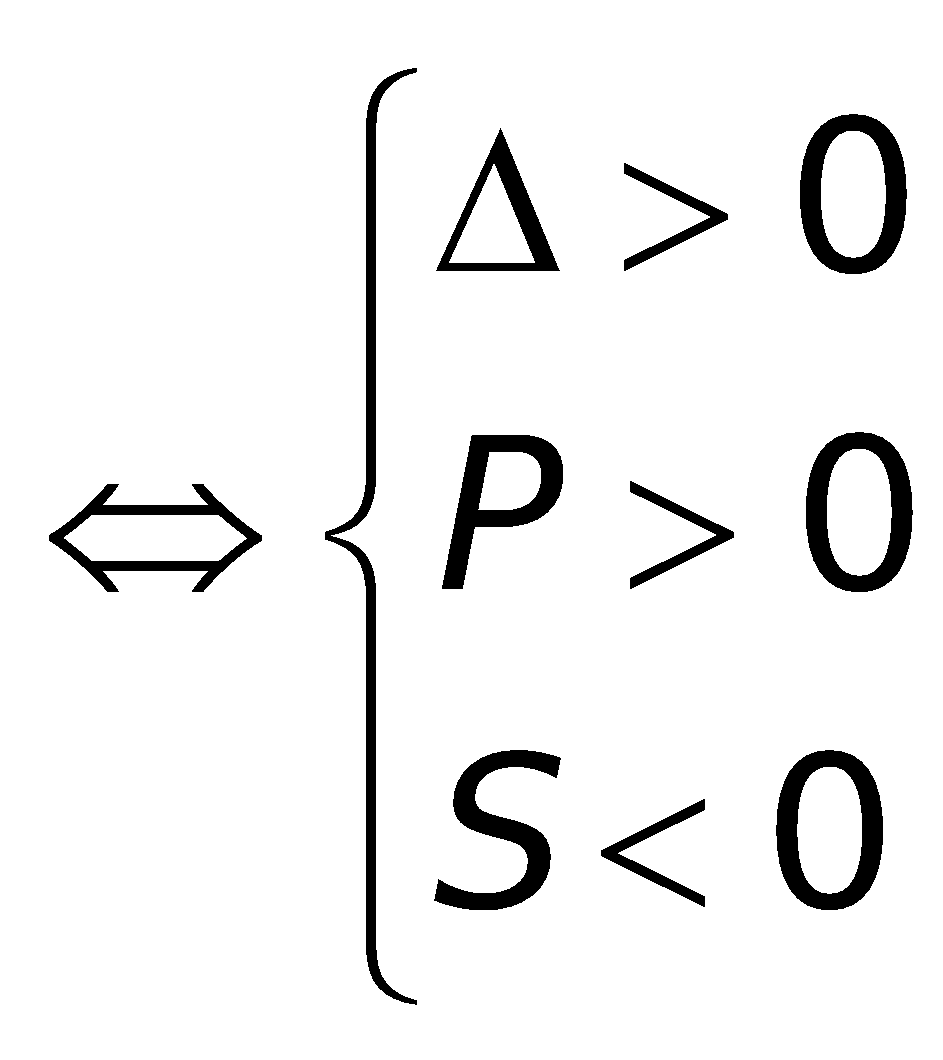
4. Những công thức về đk để tam thức không đổi vết trên R.
Cho tam thức bậc hai:
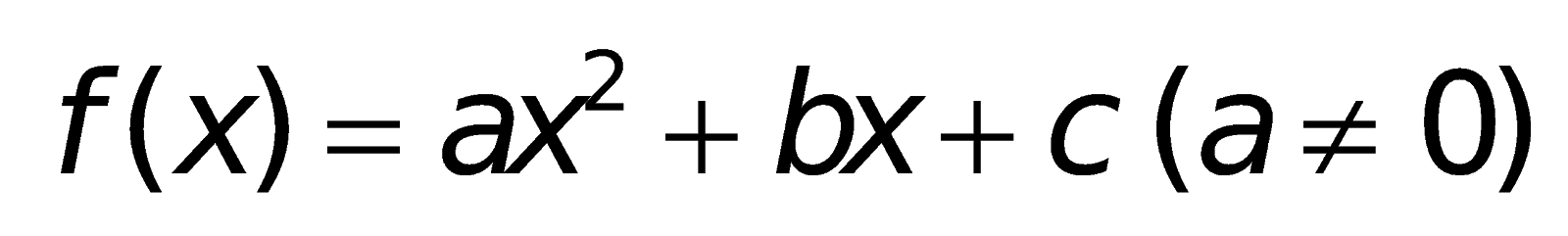
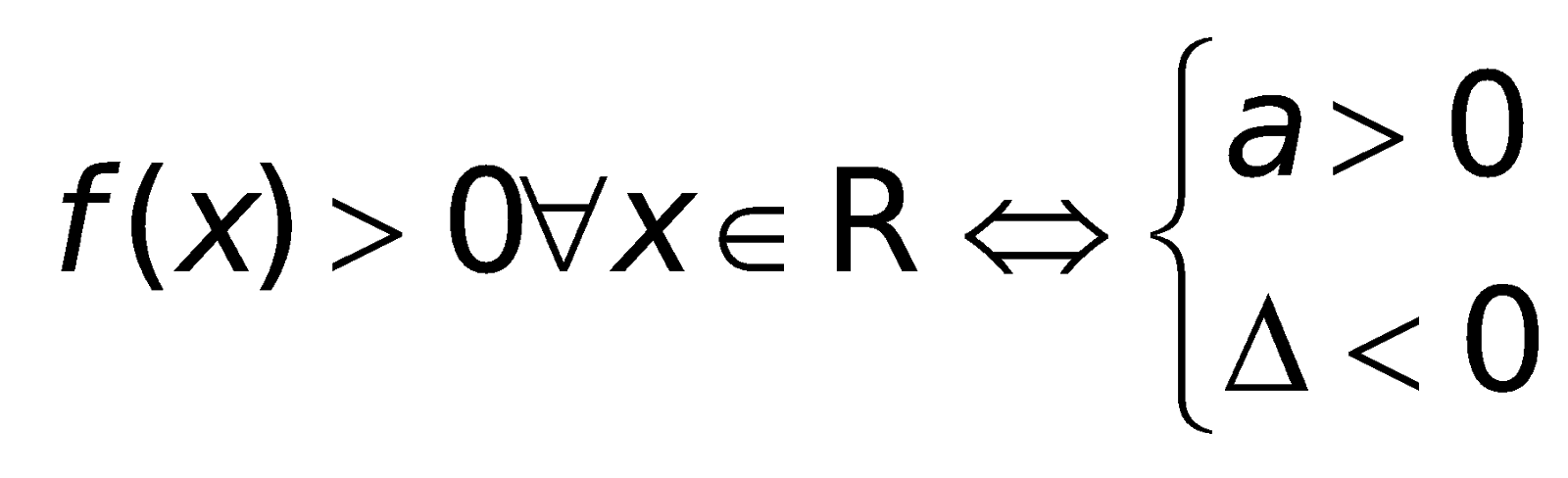
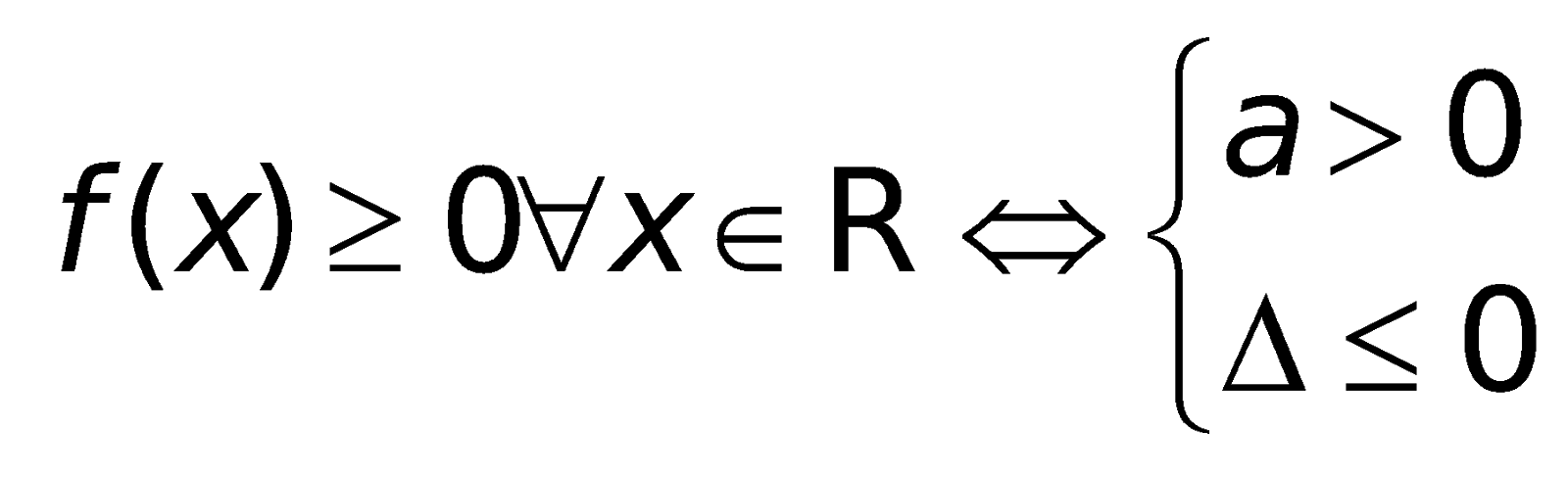
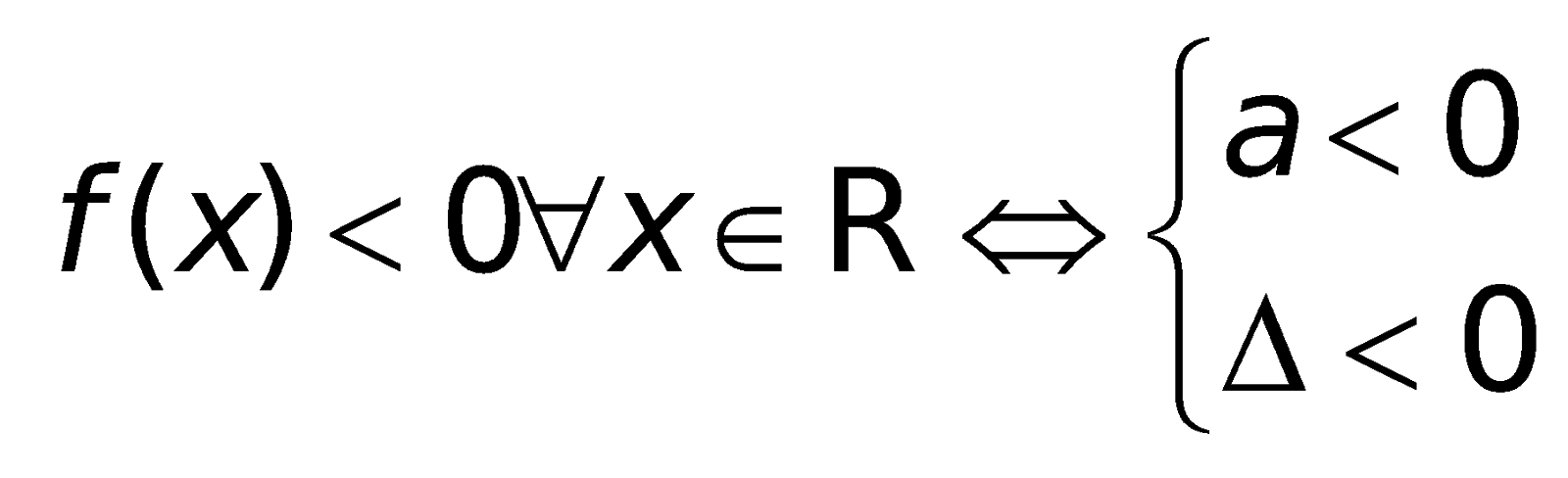
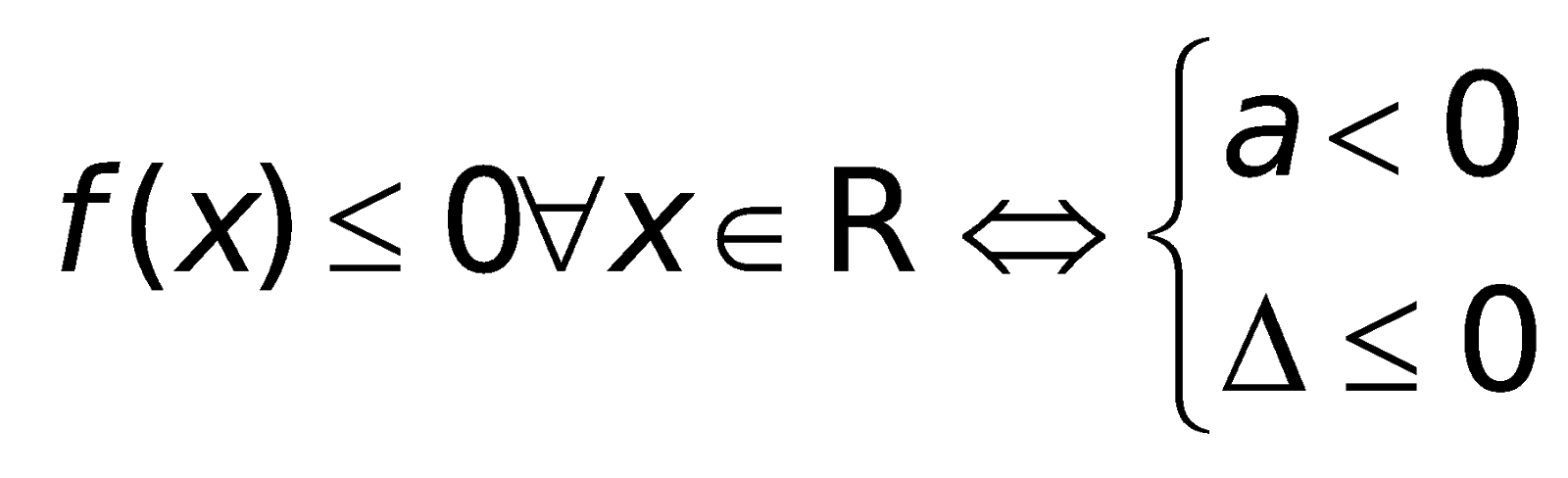
5. Những công thức toán lớp 10 về phương trình và bất phương trình đựng trị hay đối
a. Phương trình :
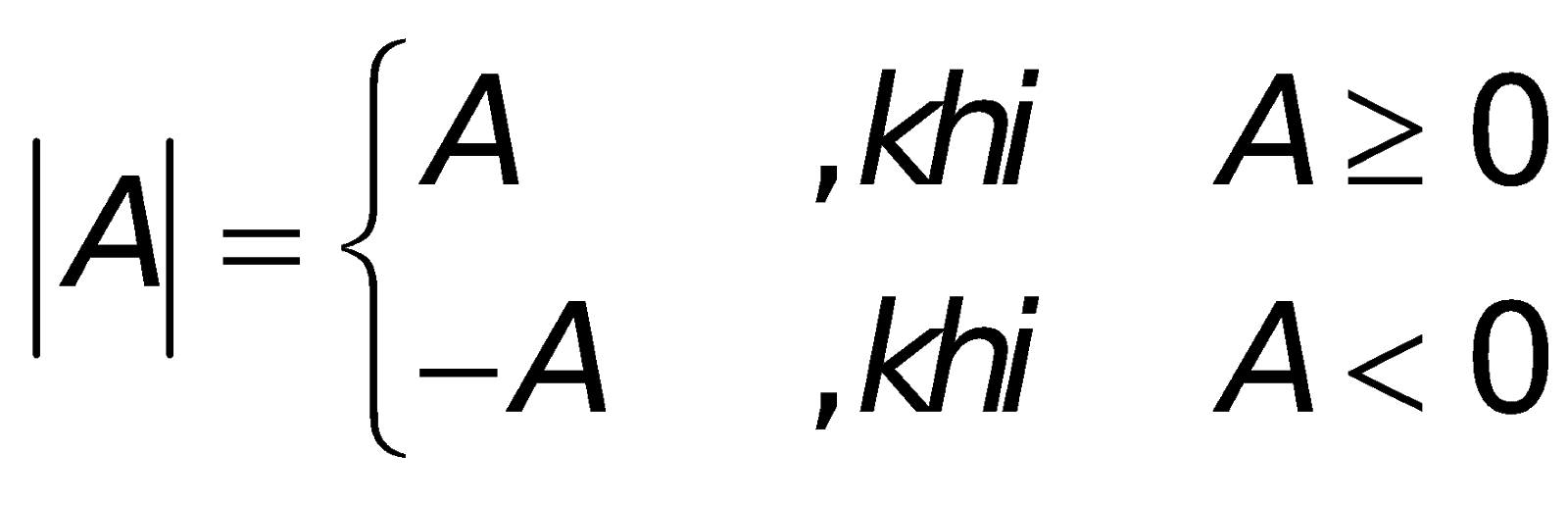
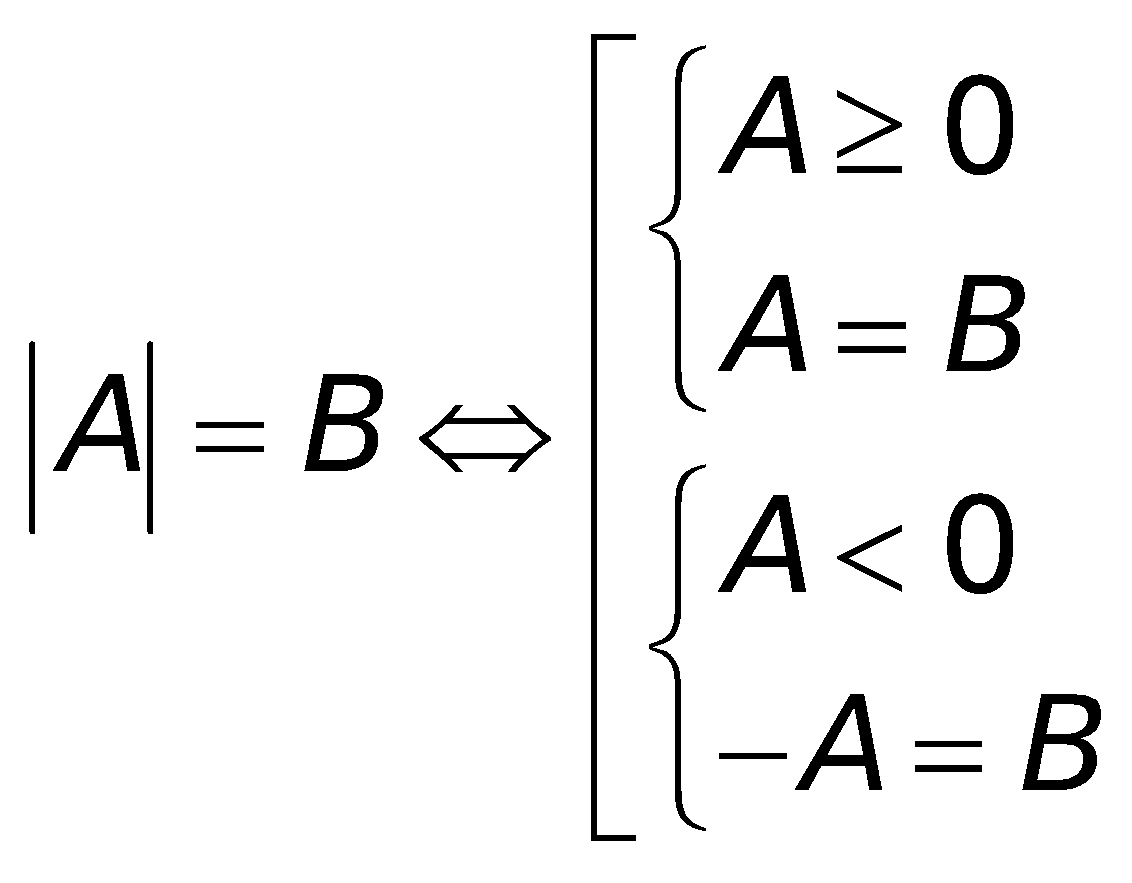
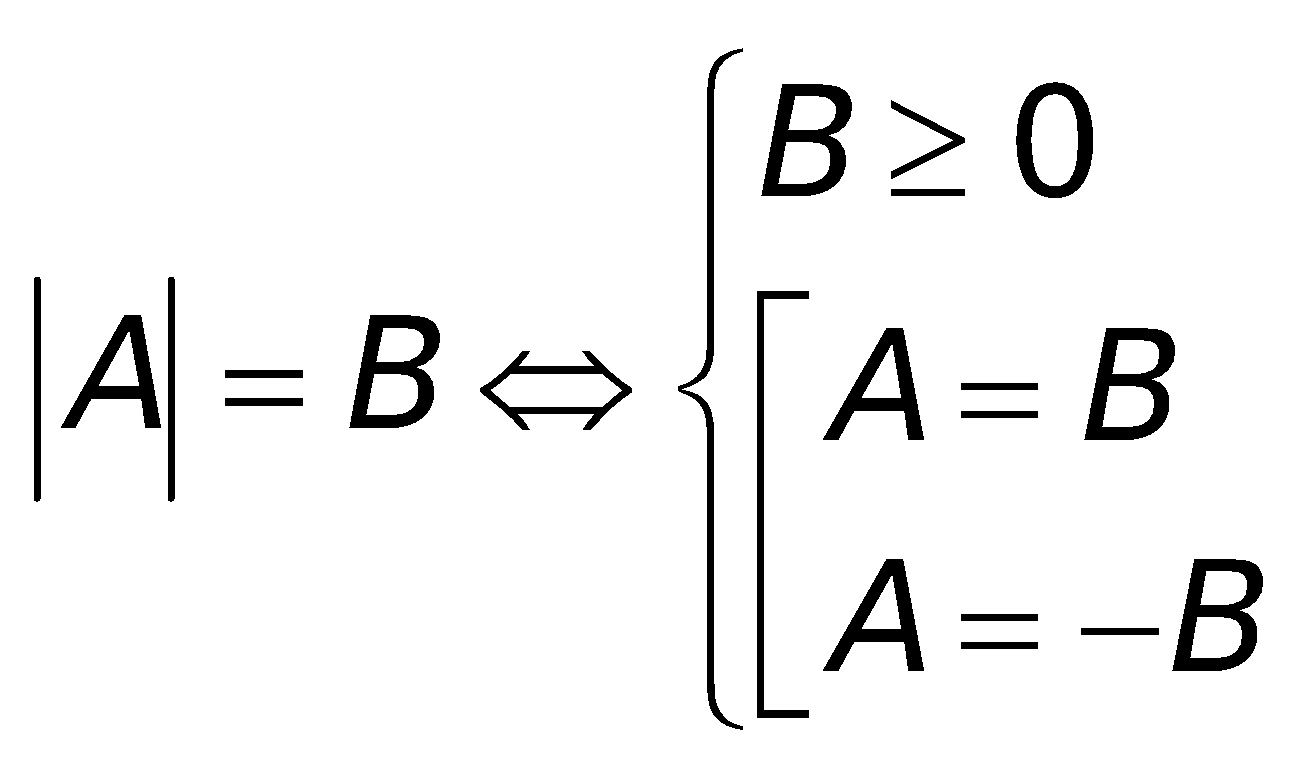
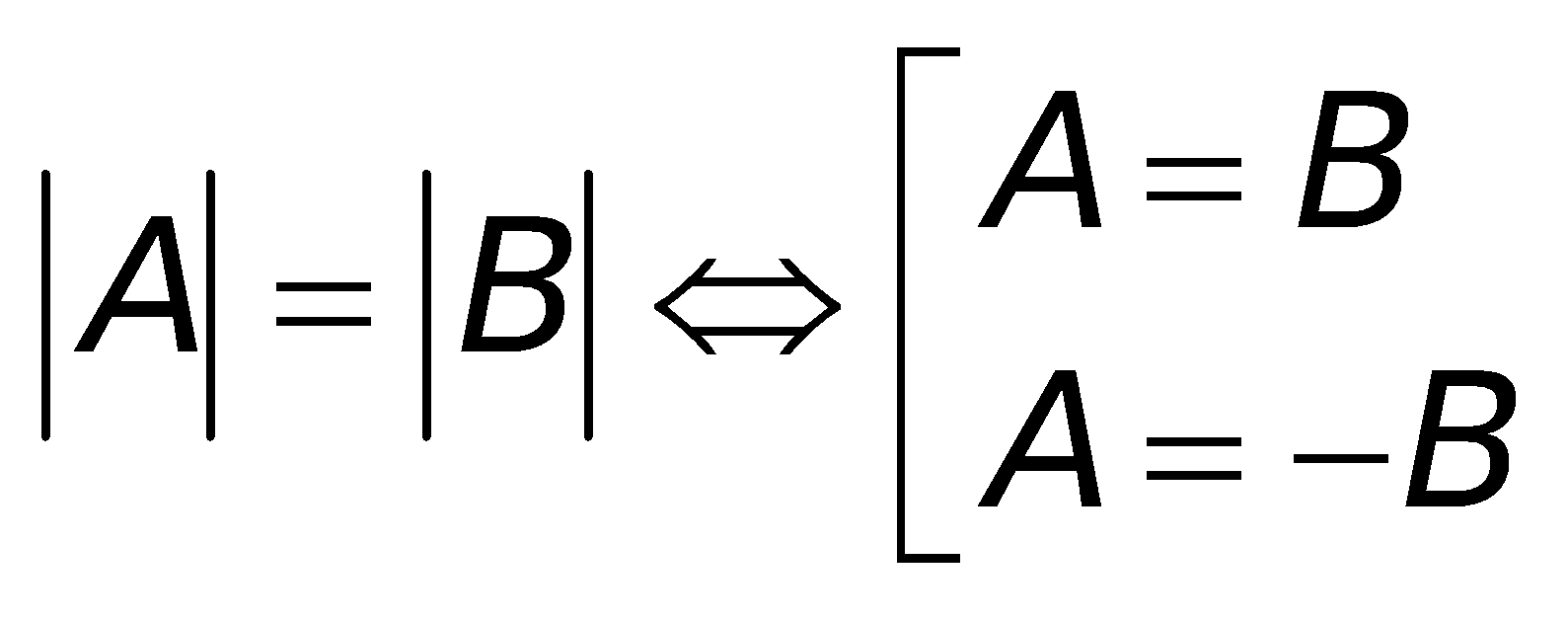
b. Bất phương trình:
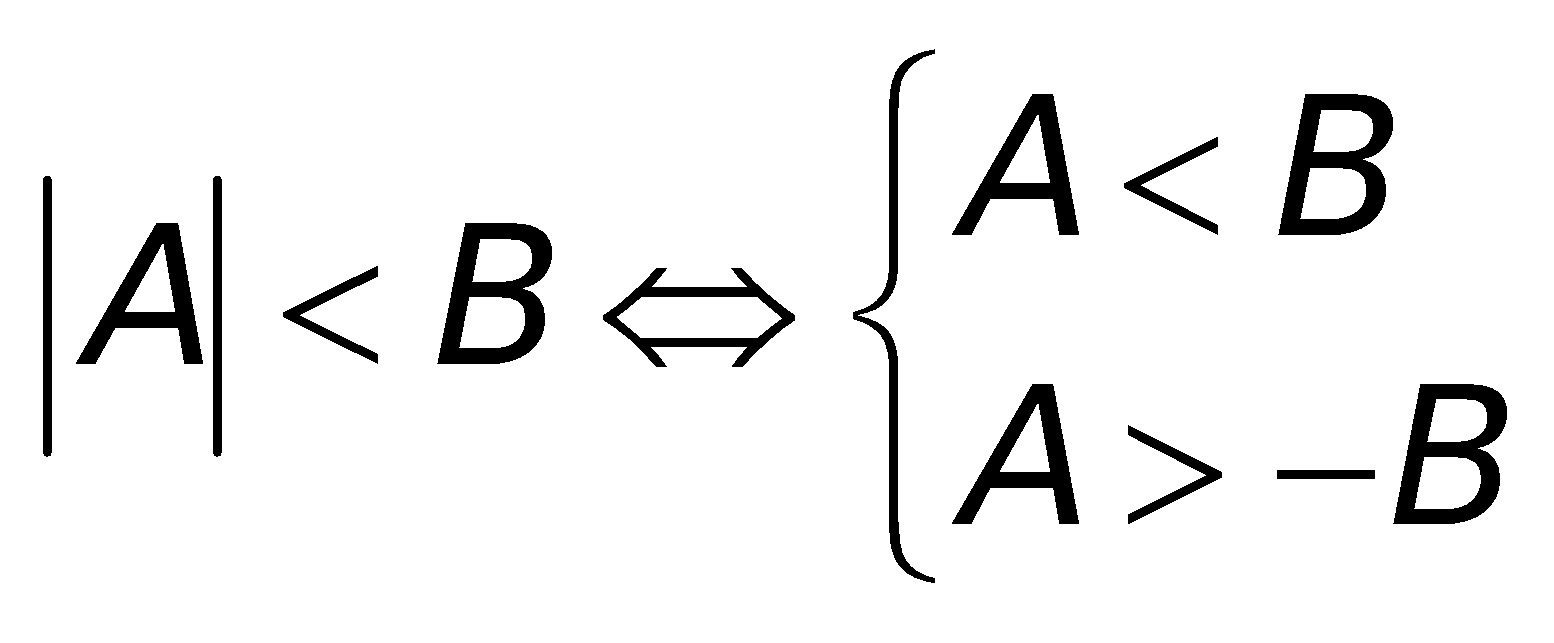
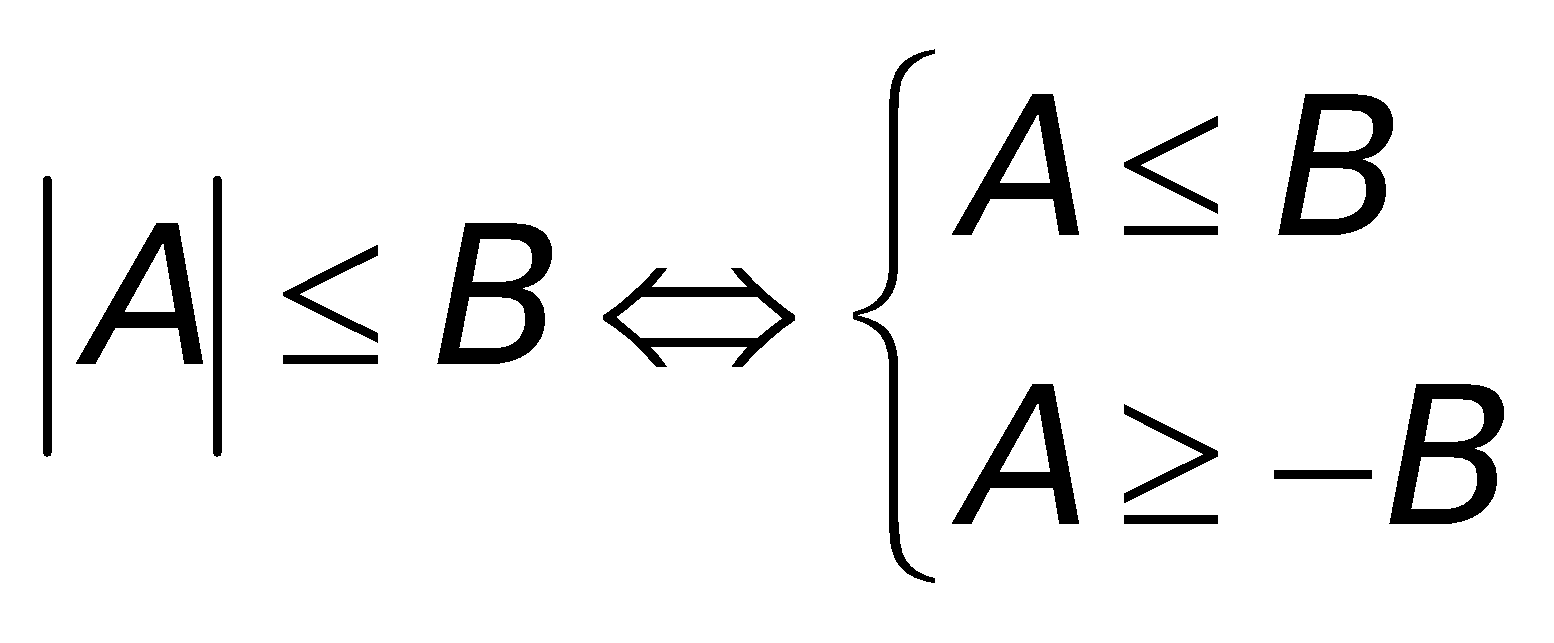
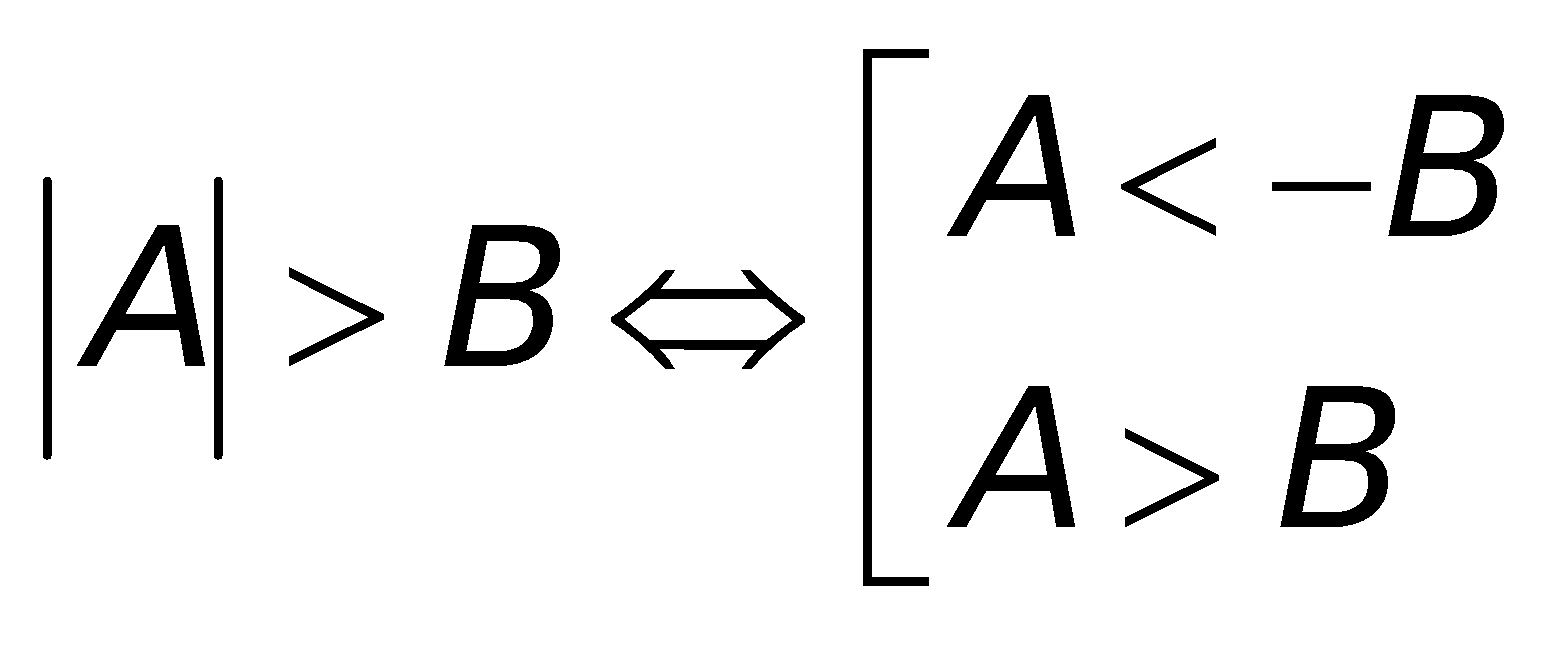
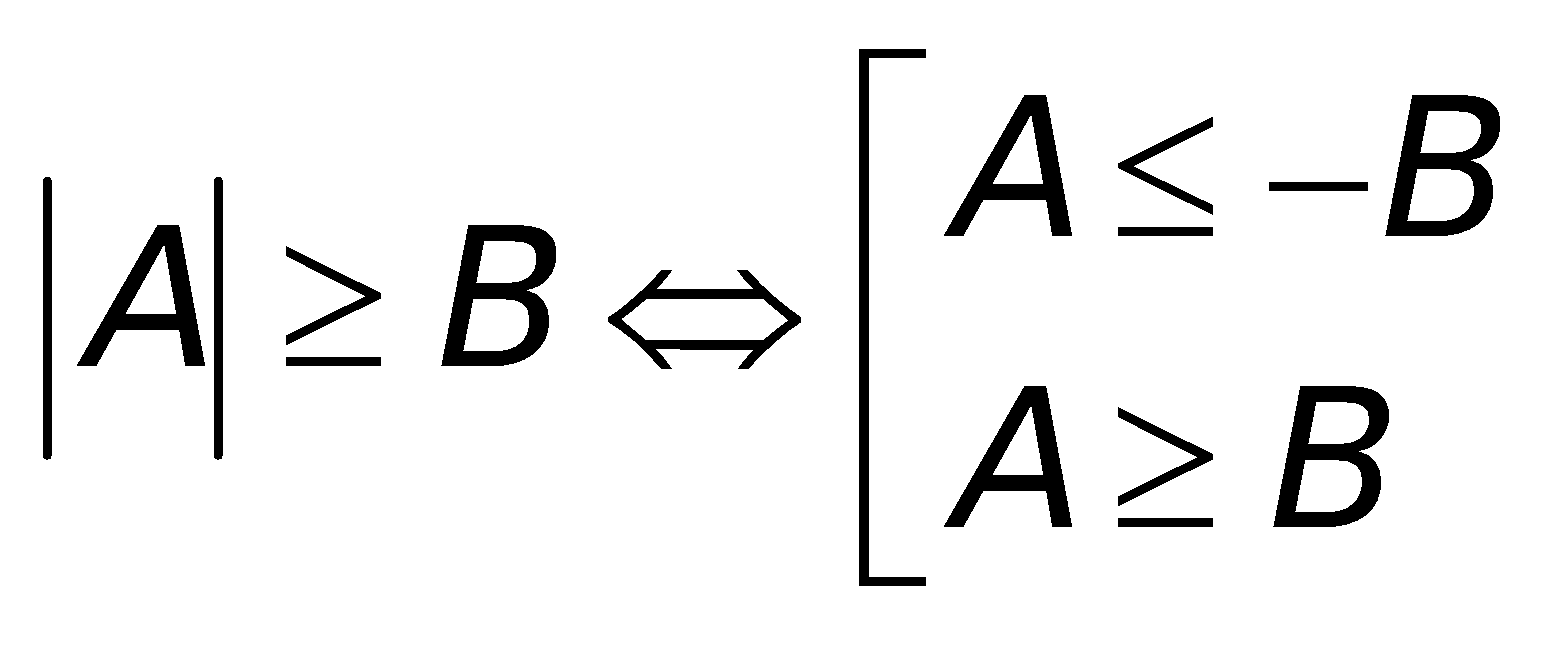
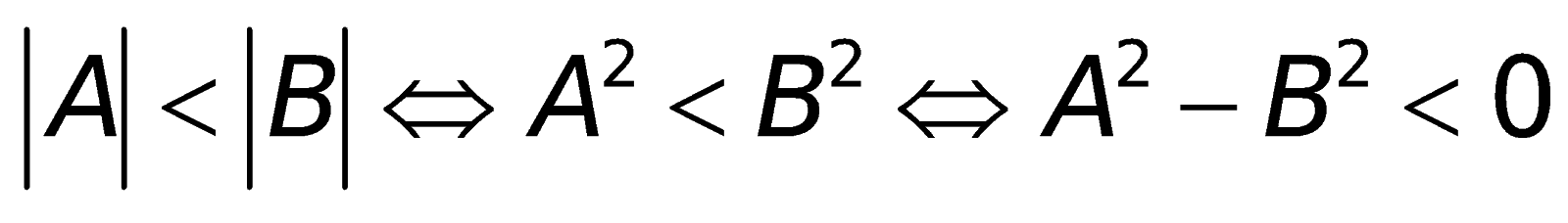
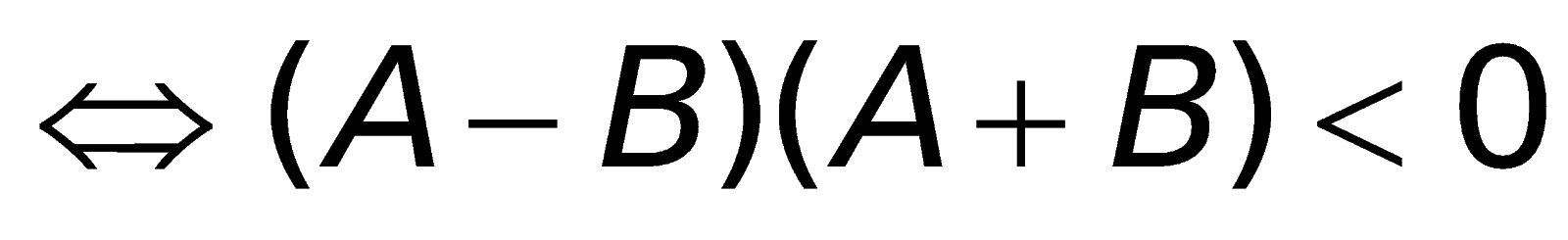
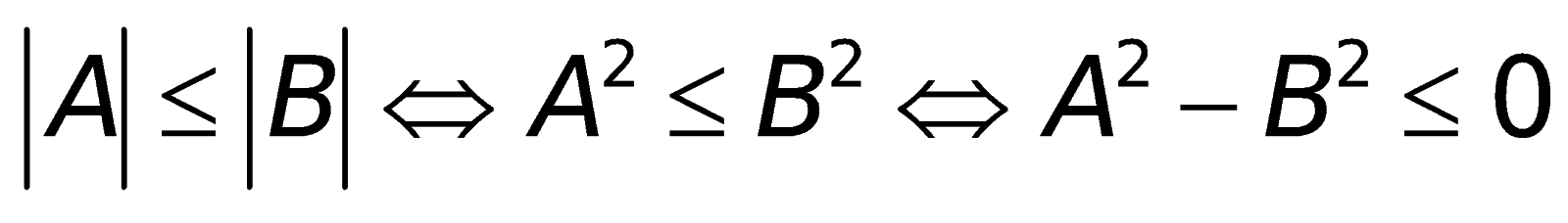
6. Những công thức toán lớp 10 về phương trình cùng bất phương trình chứa đằng sau dấu căn bậc hai
a. Phương trình:
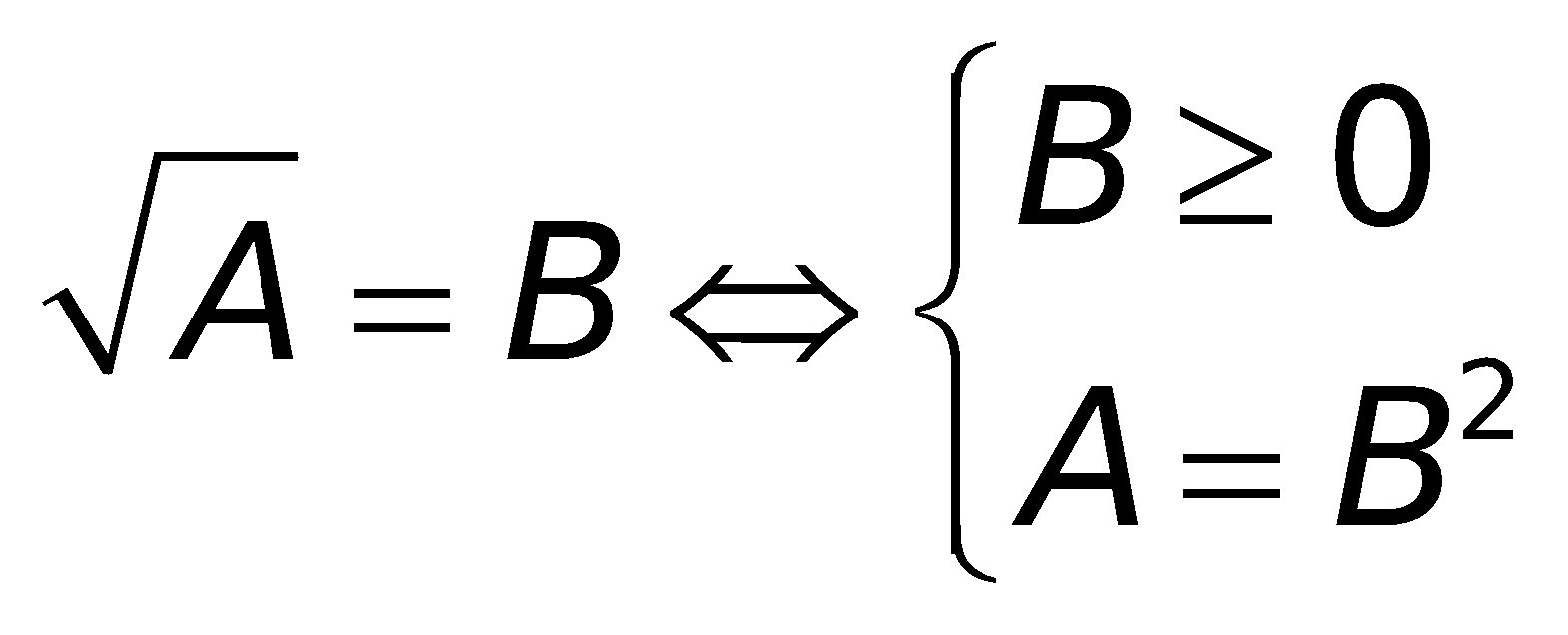
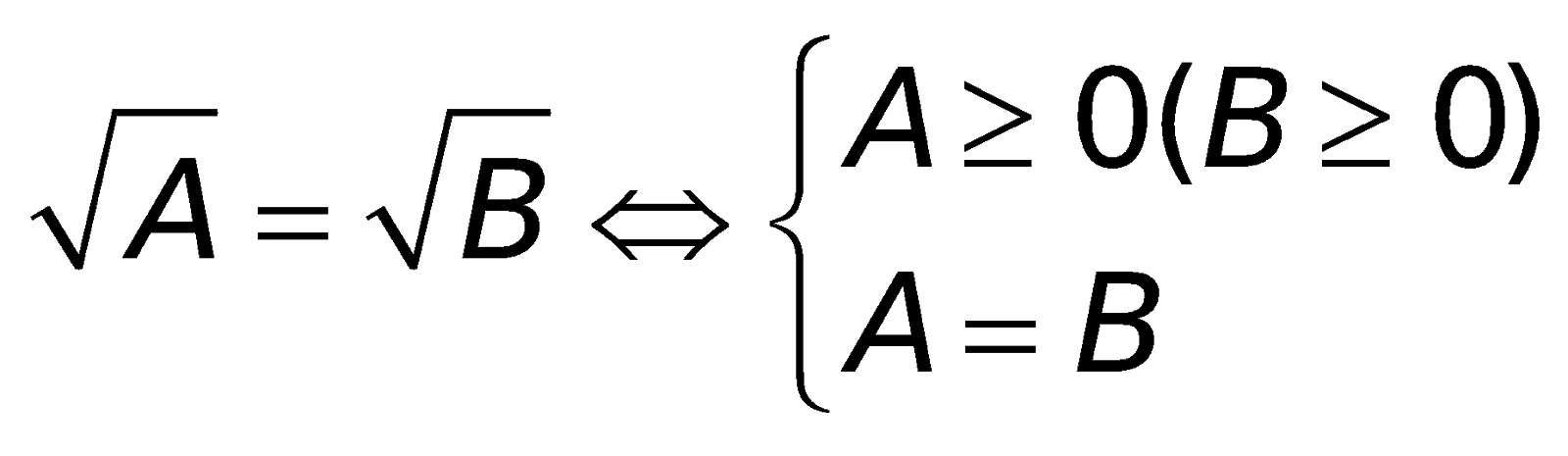
b. Bất phương trình:
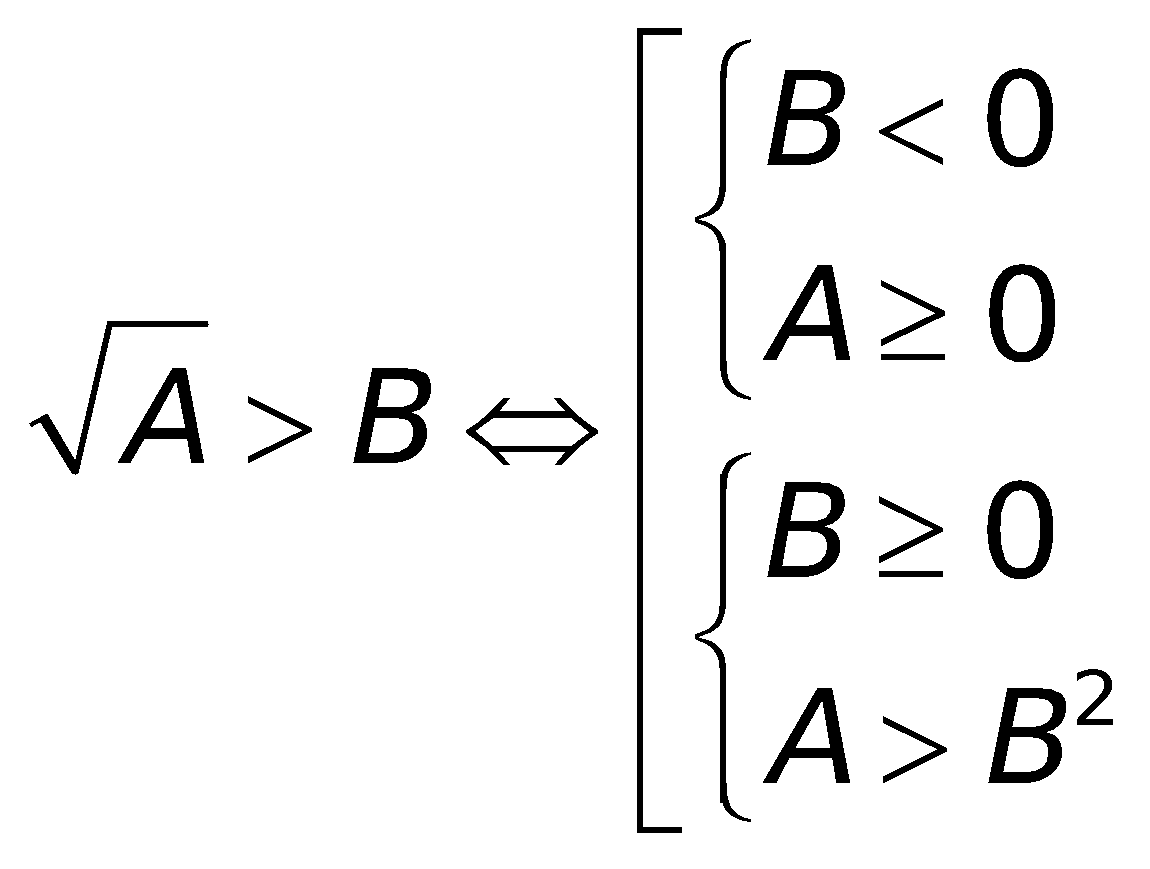
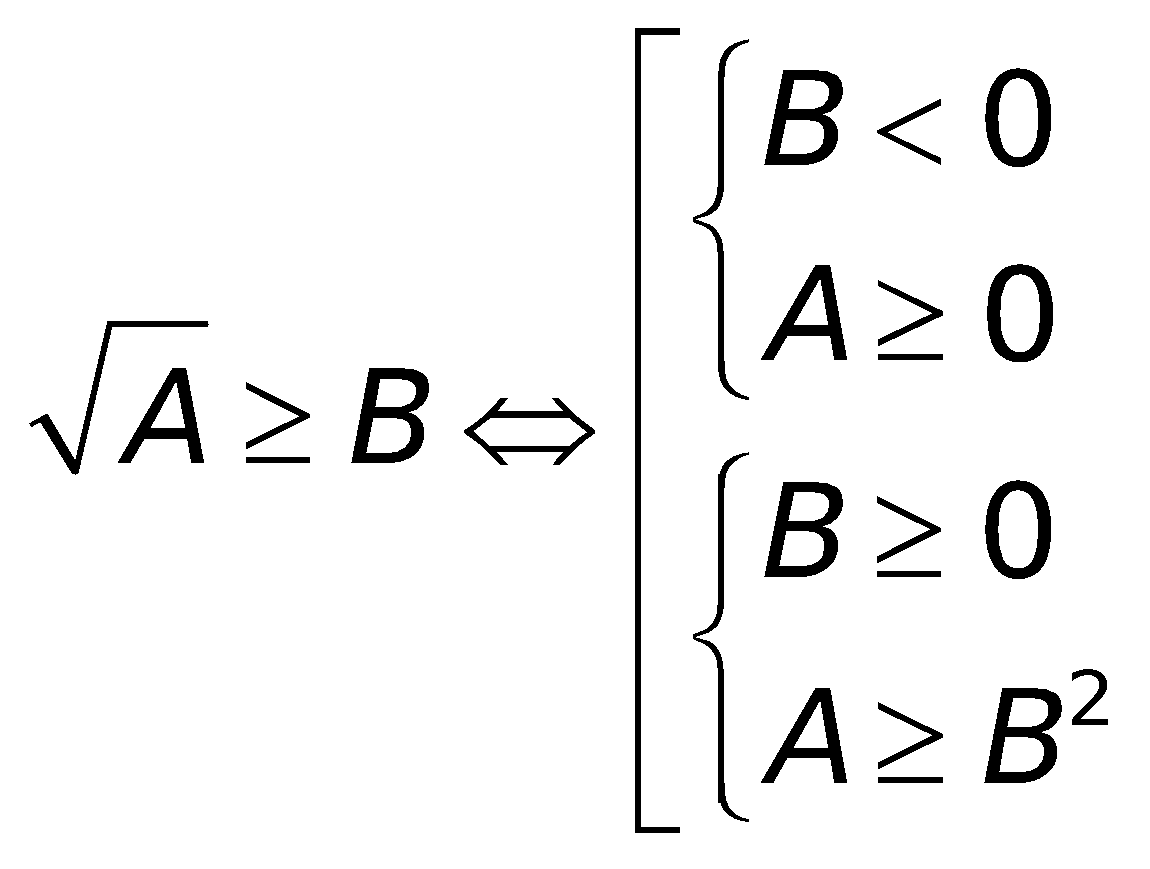
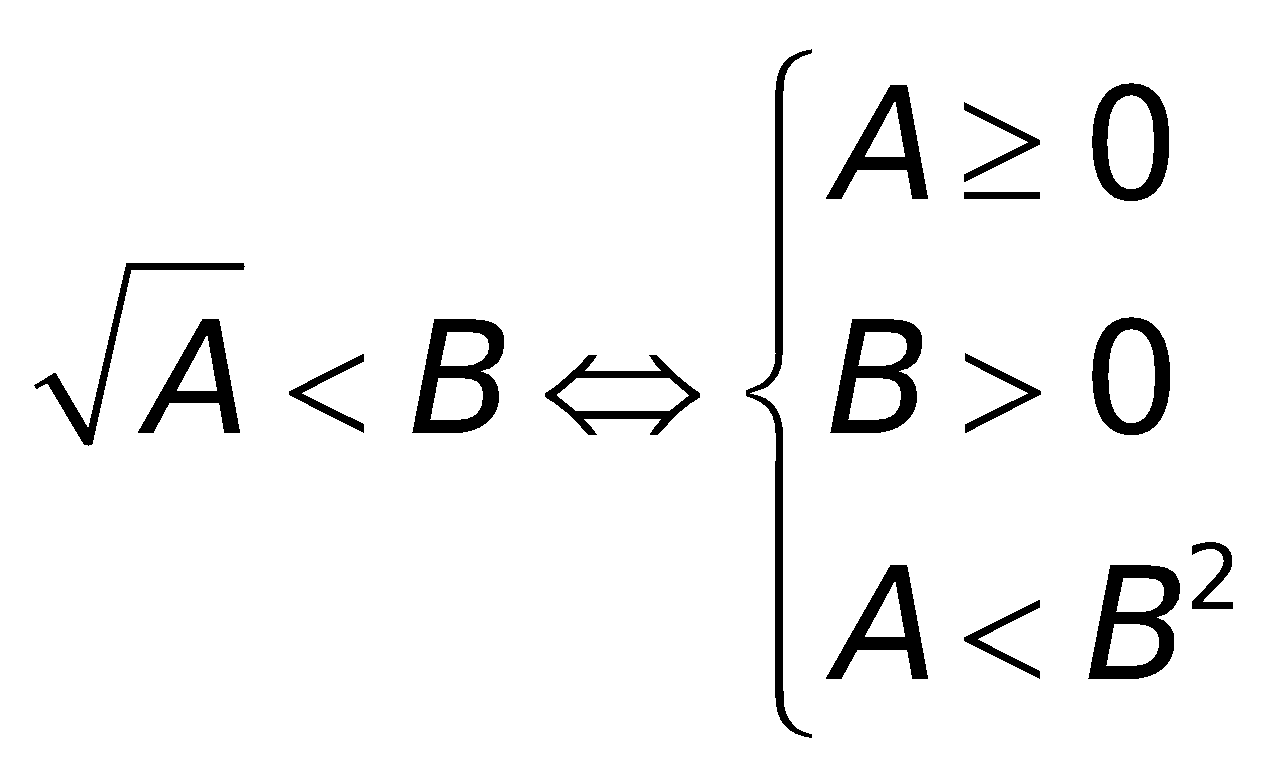
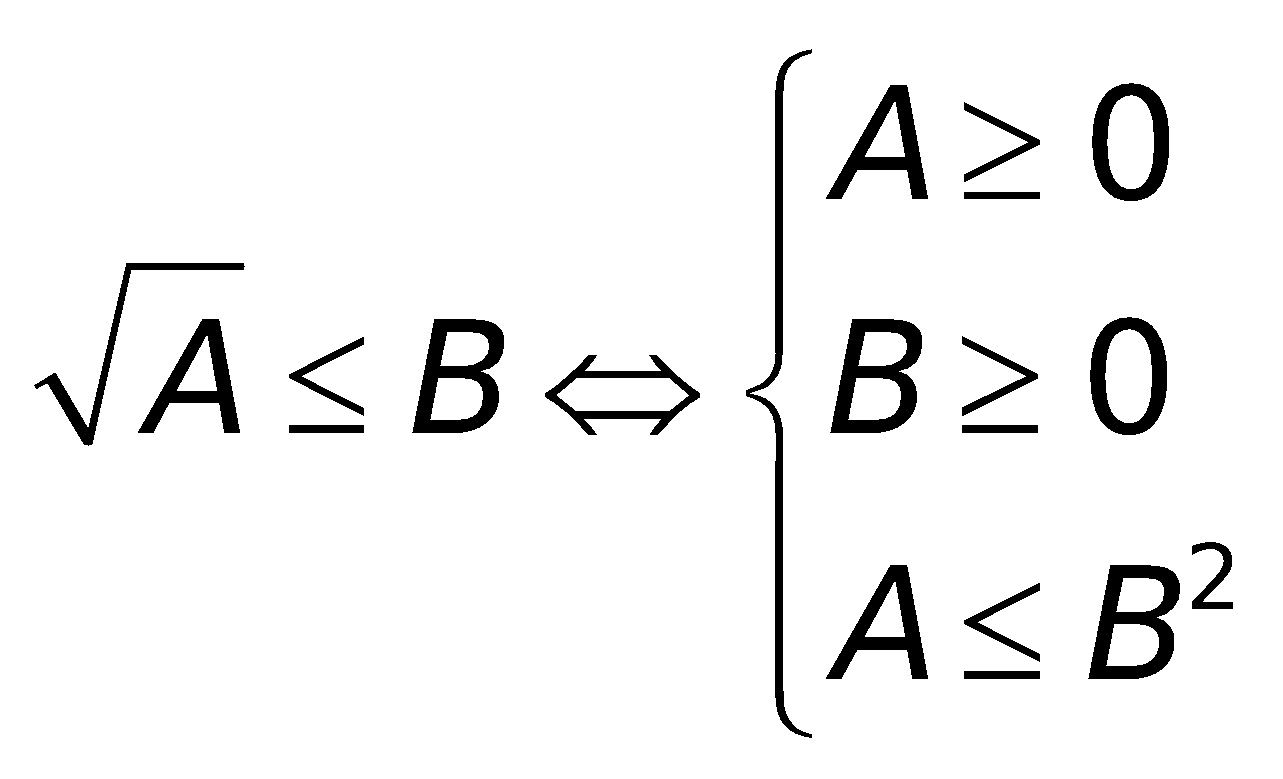
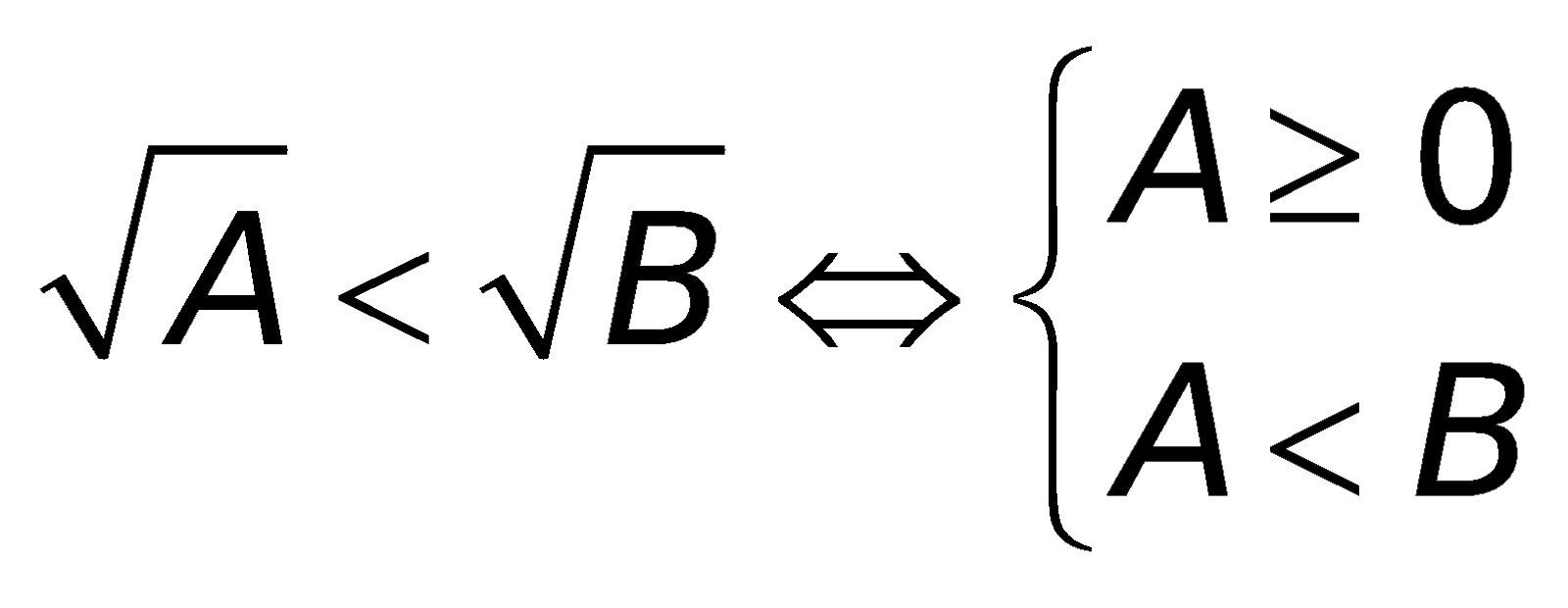
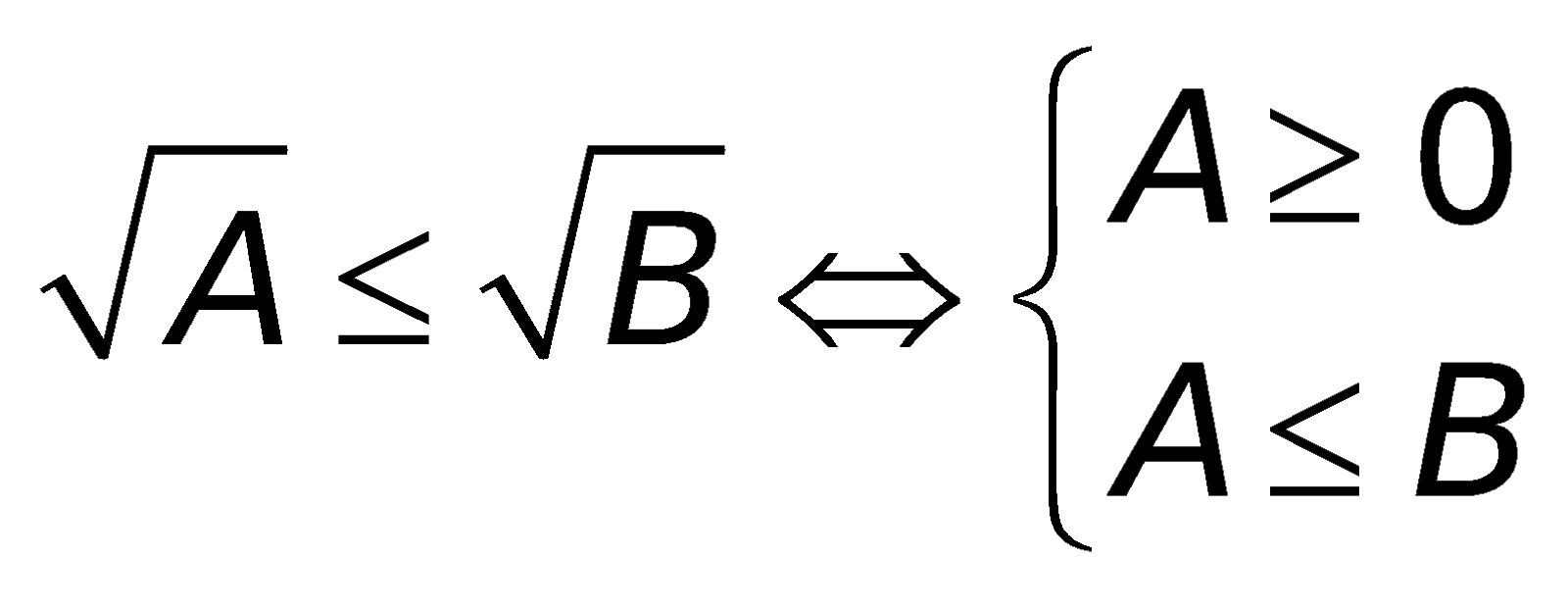
7. Những công thức toán lớp 10 lượng giác
a. Định nghĩa giá trị lượng giác: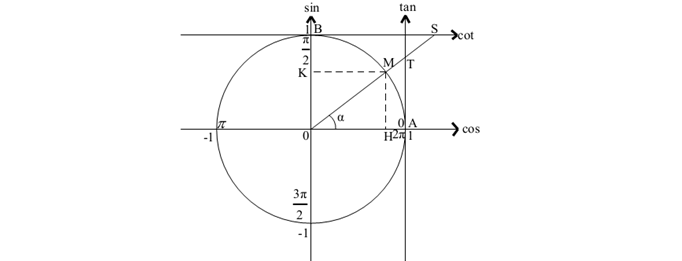
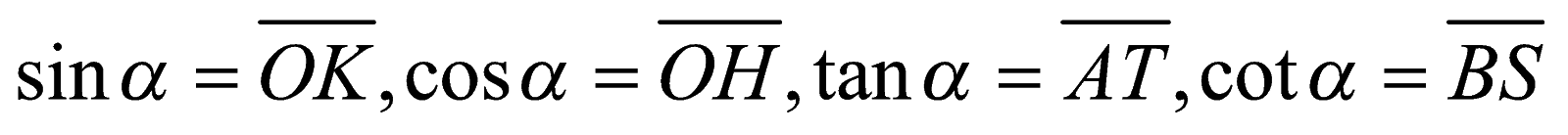
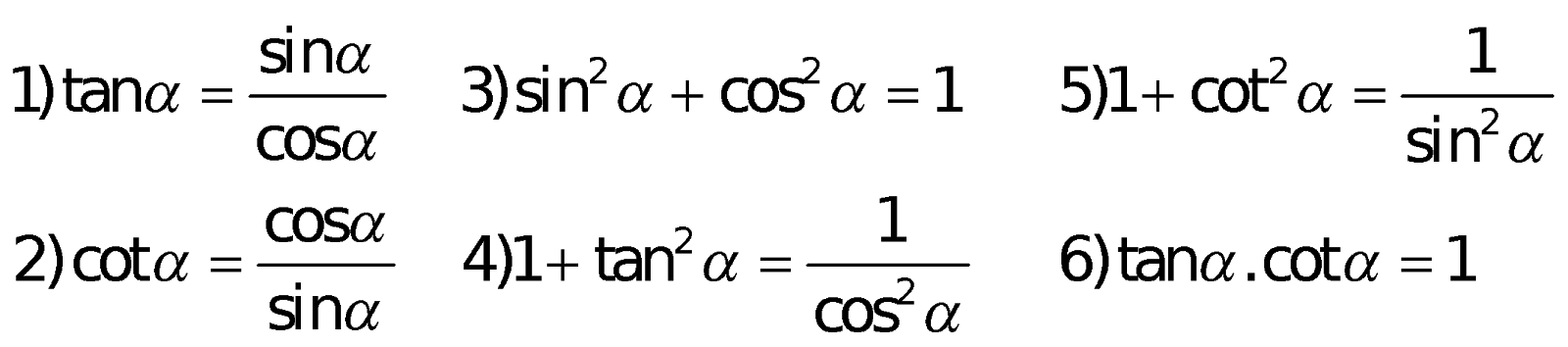
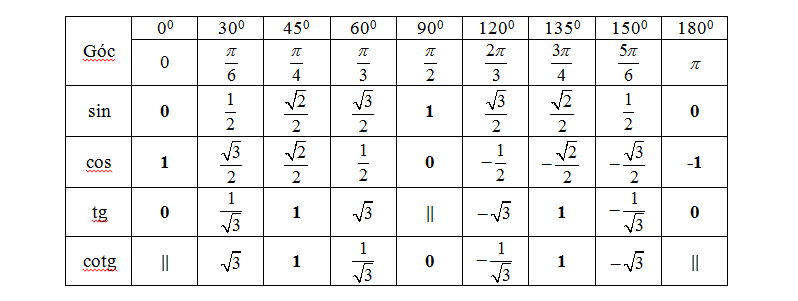
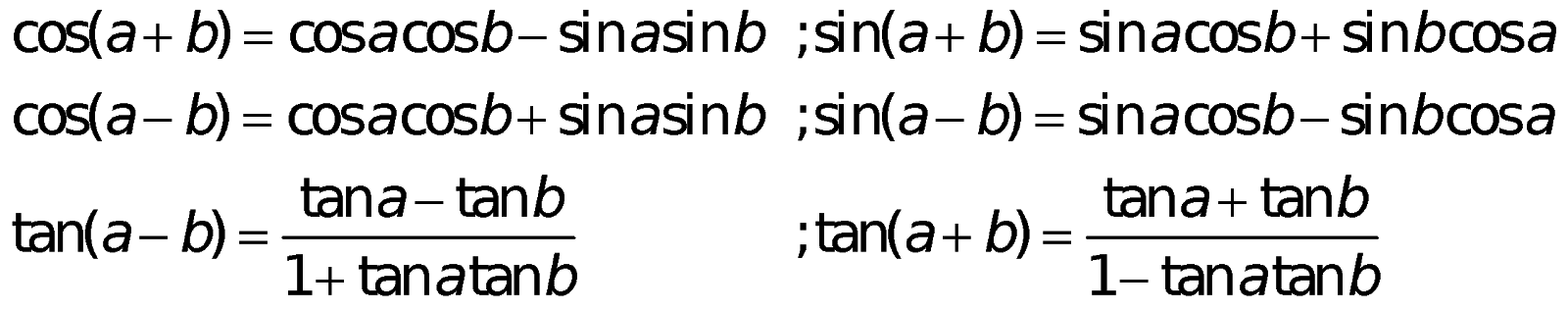
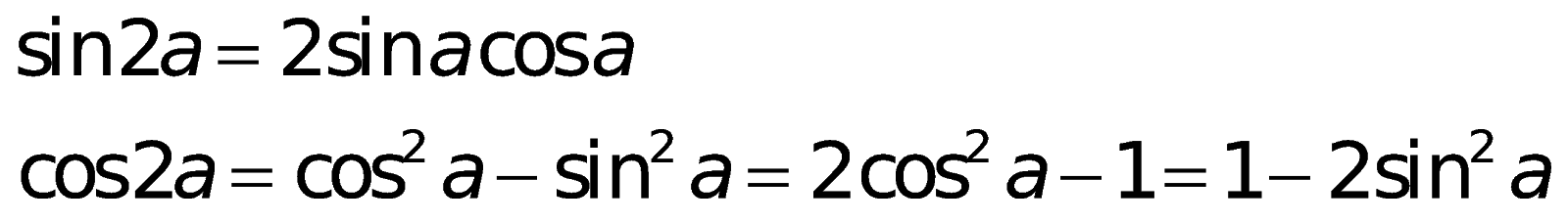
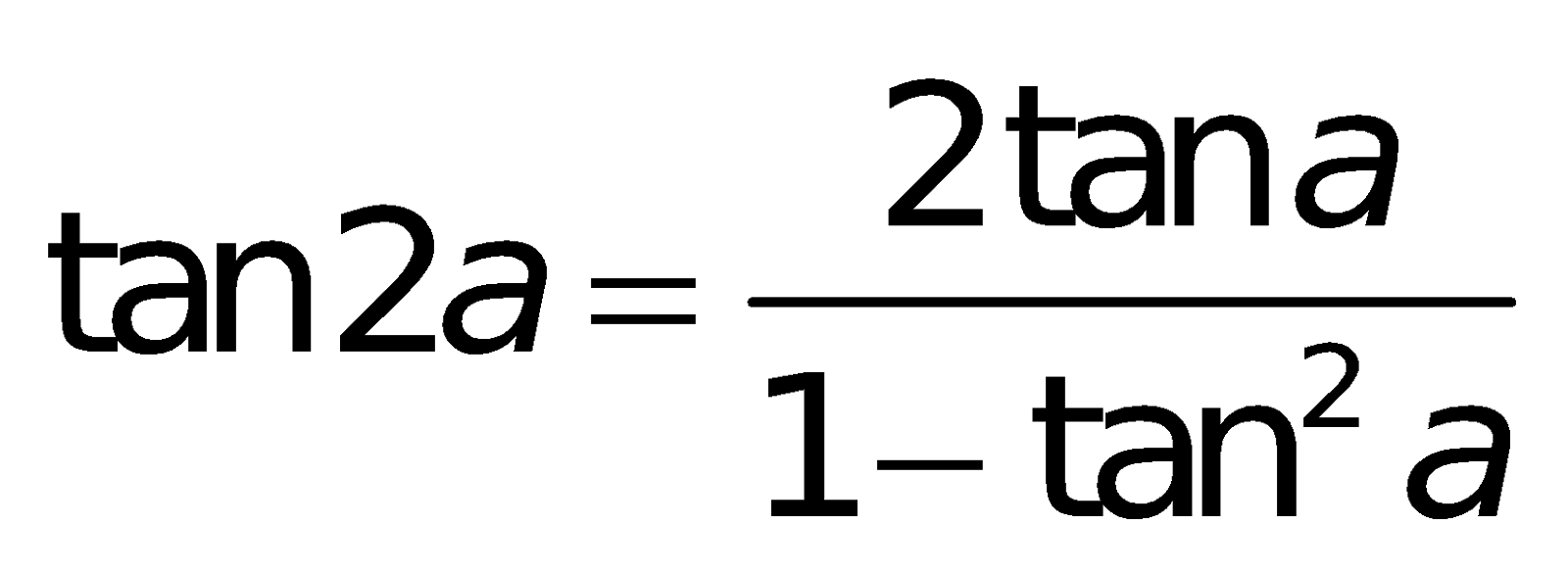
f. Cách làm hạ bậc:
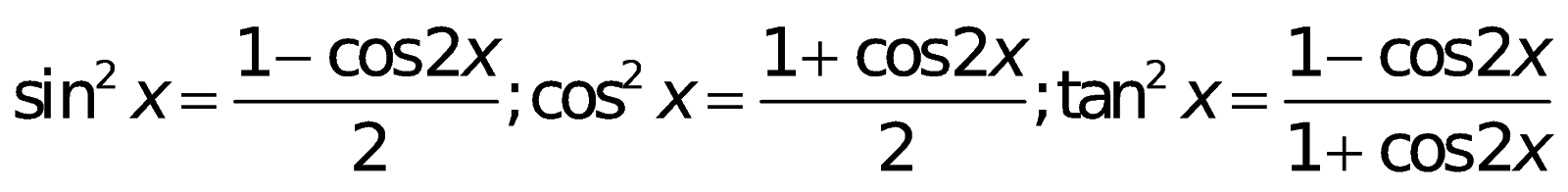
g. Công thức nhân ba:

h. Công thức đổi khác tích thành tổng:
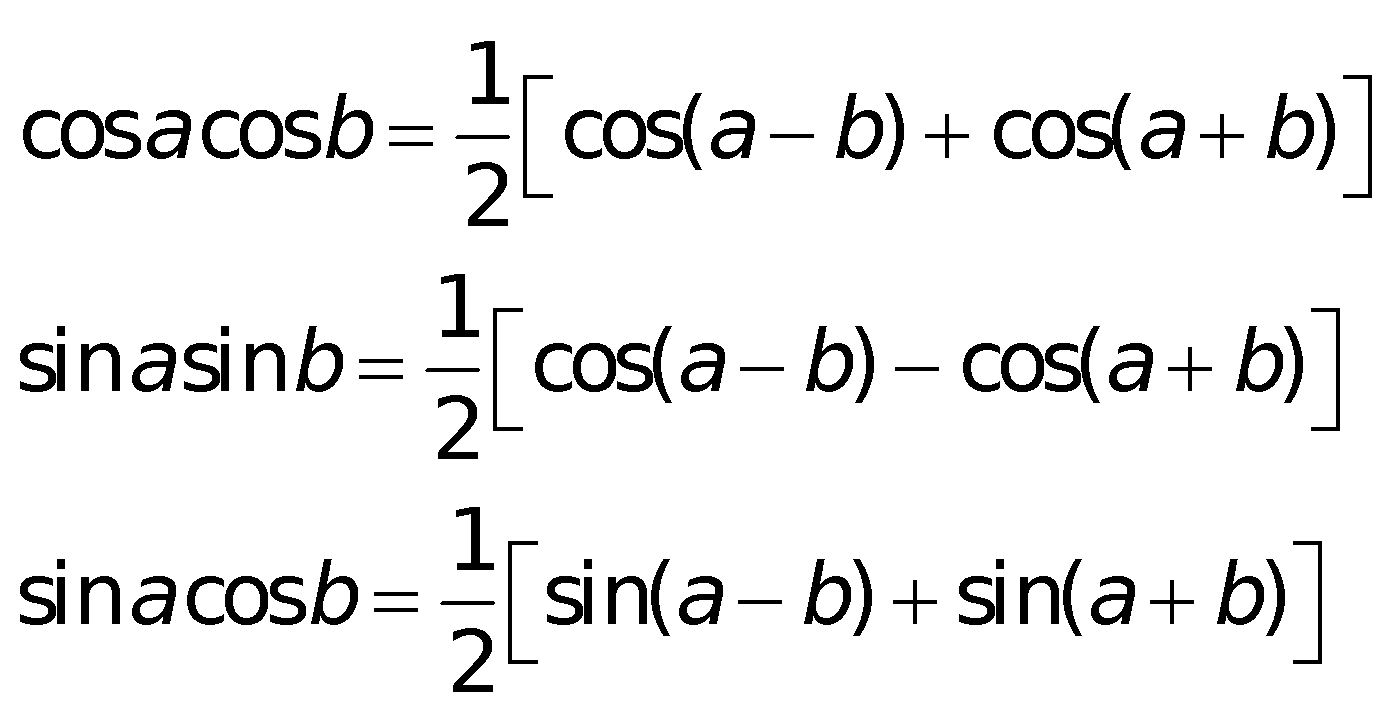
i. Công thức đổi khác tổng thành tích:
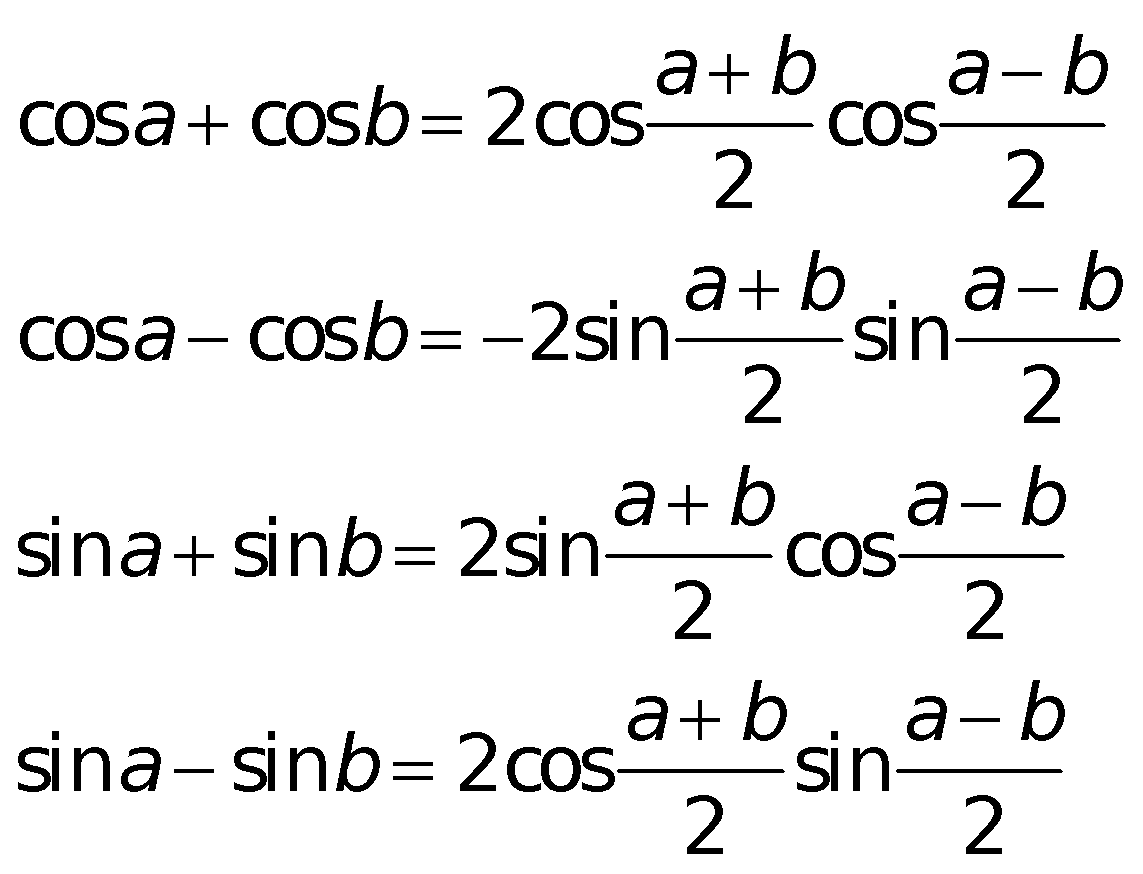
k. Cung liên kết: Sin – bù; cos – đối; phụ – chéo; hơn nhát


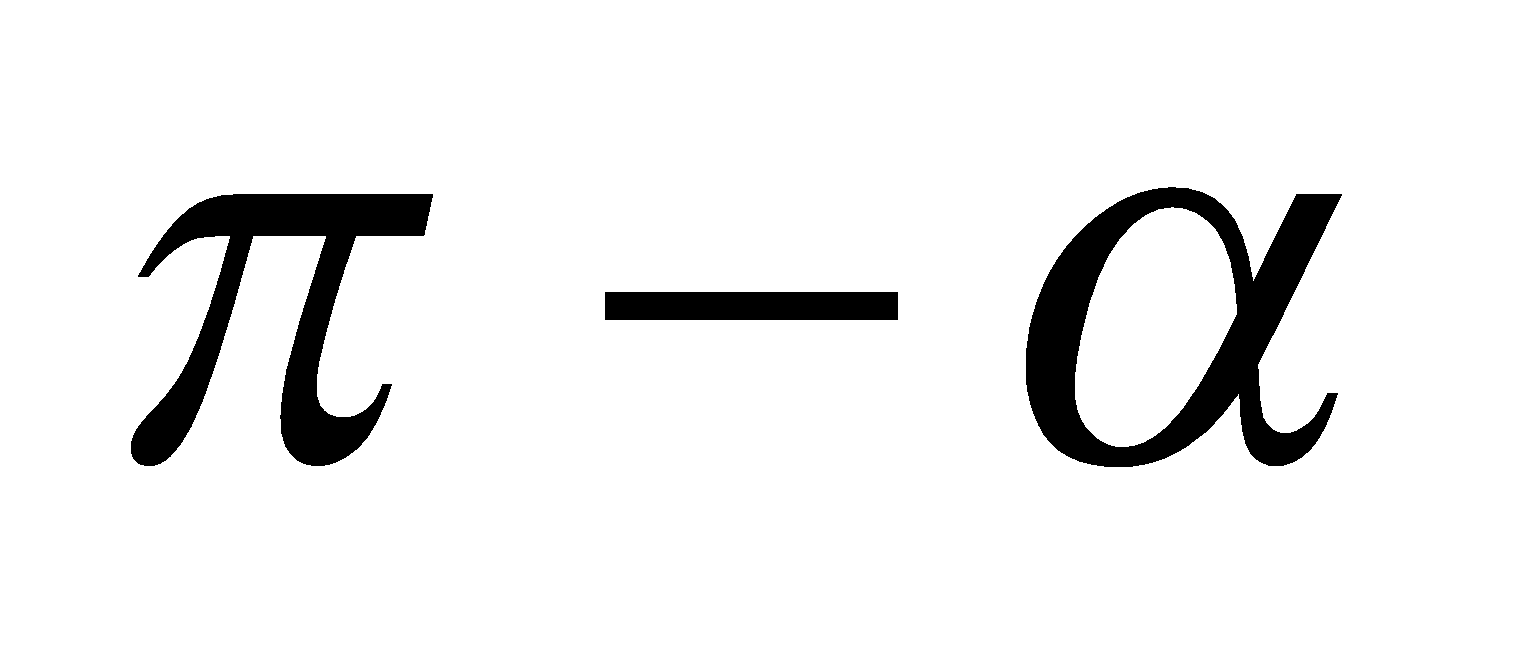
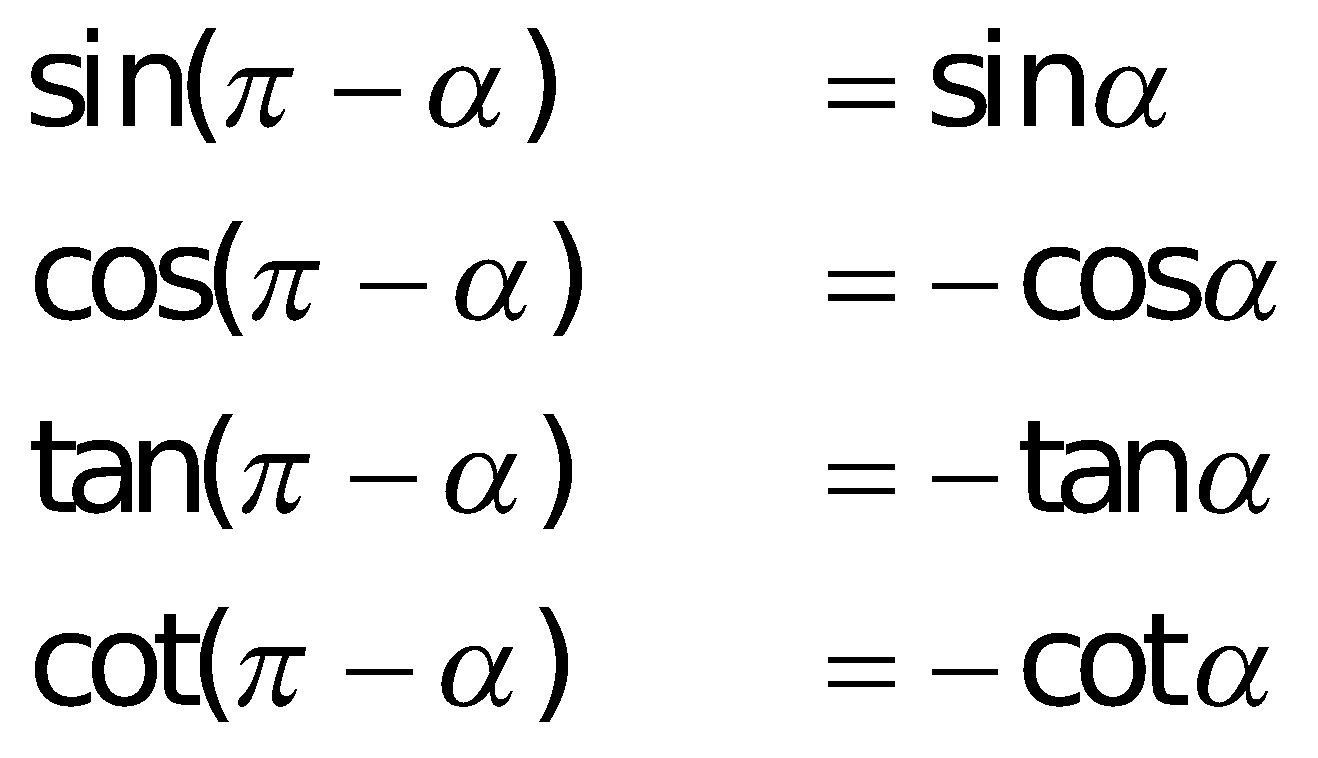

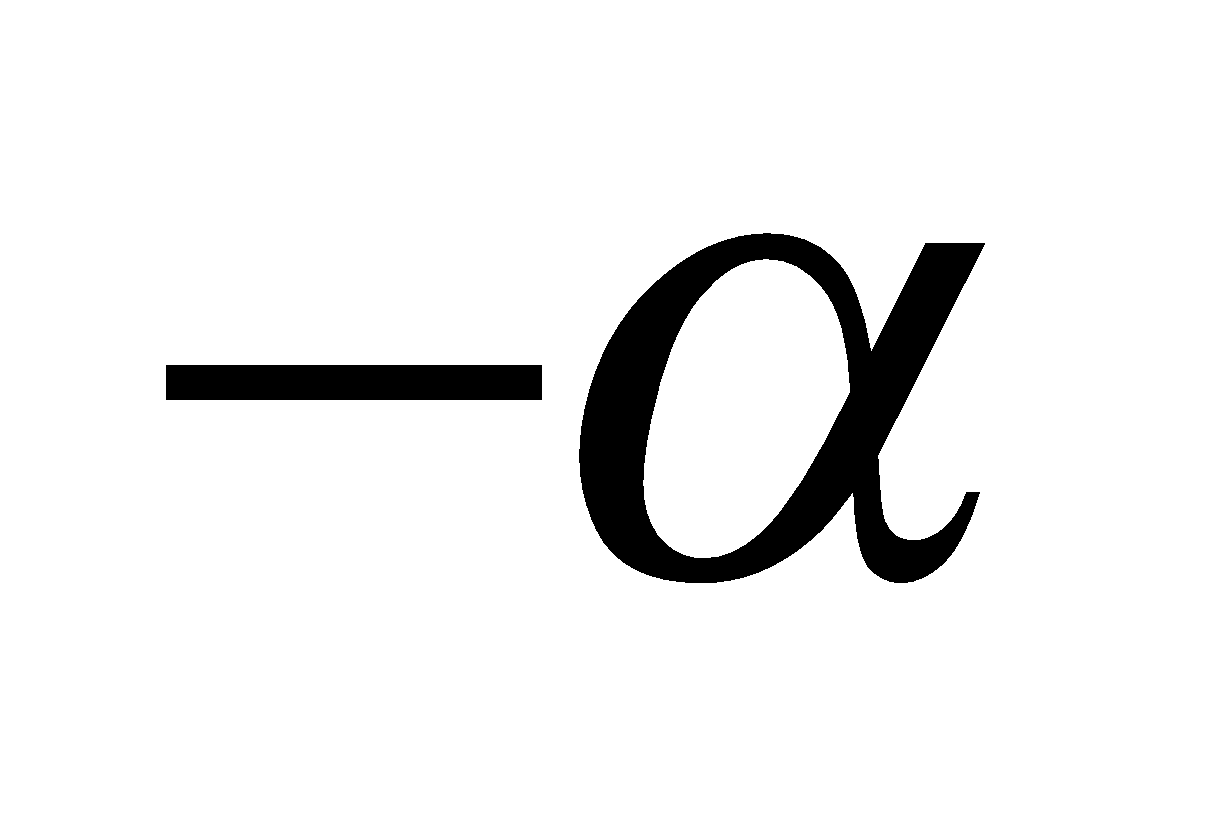
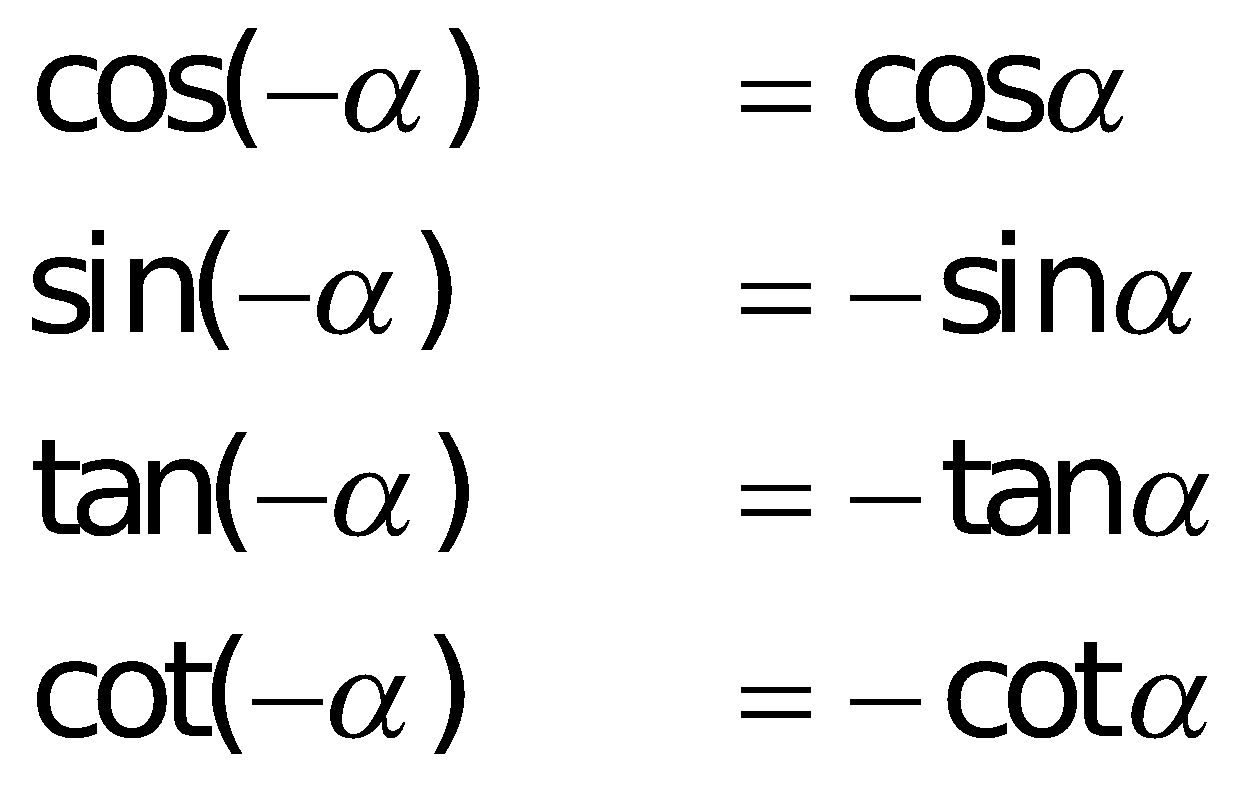

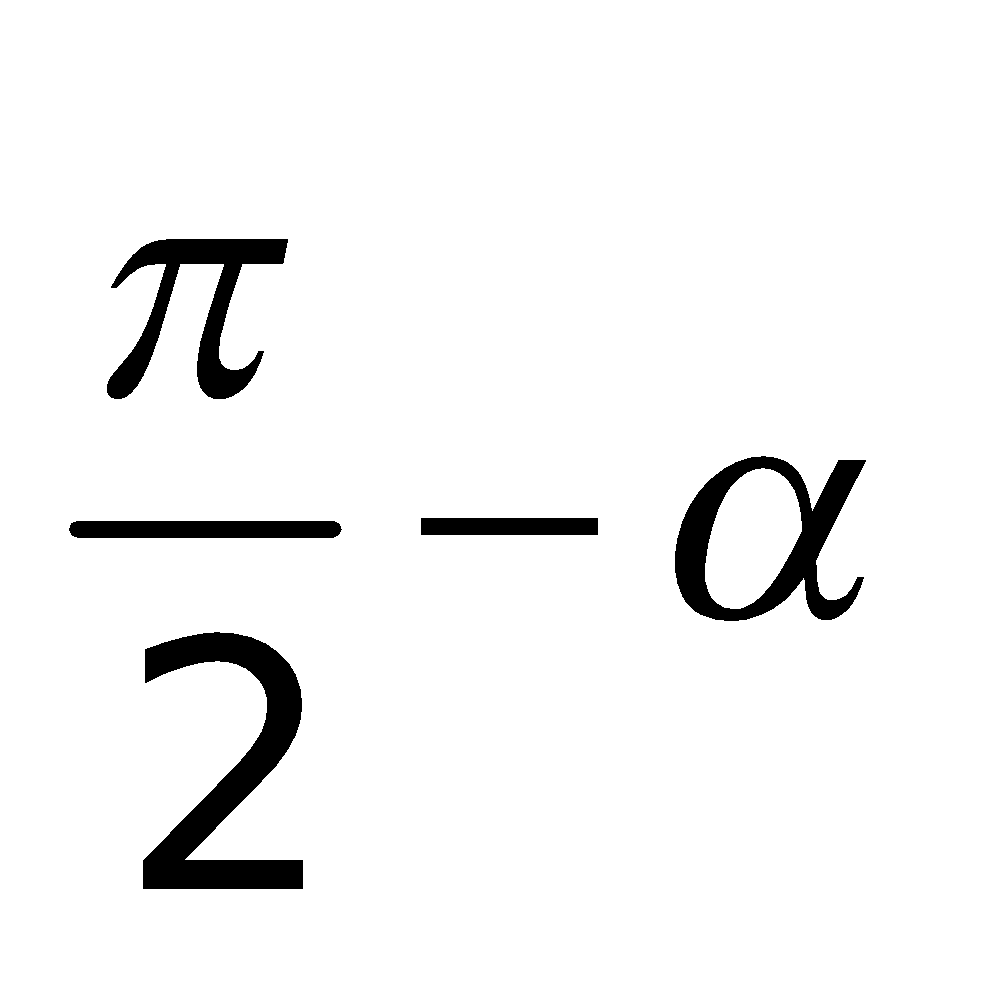
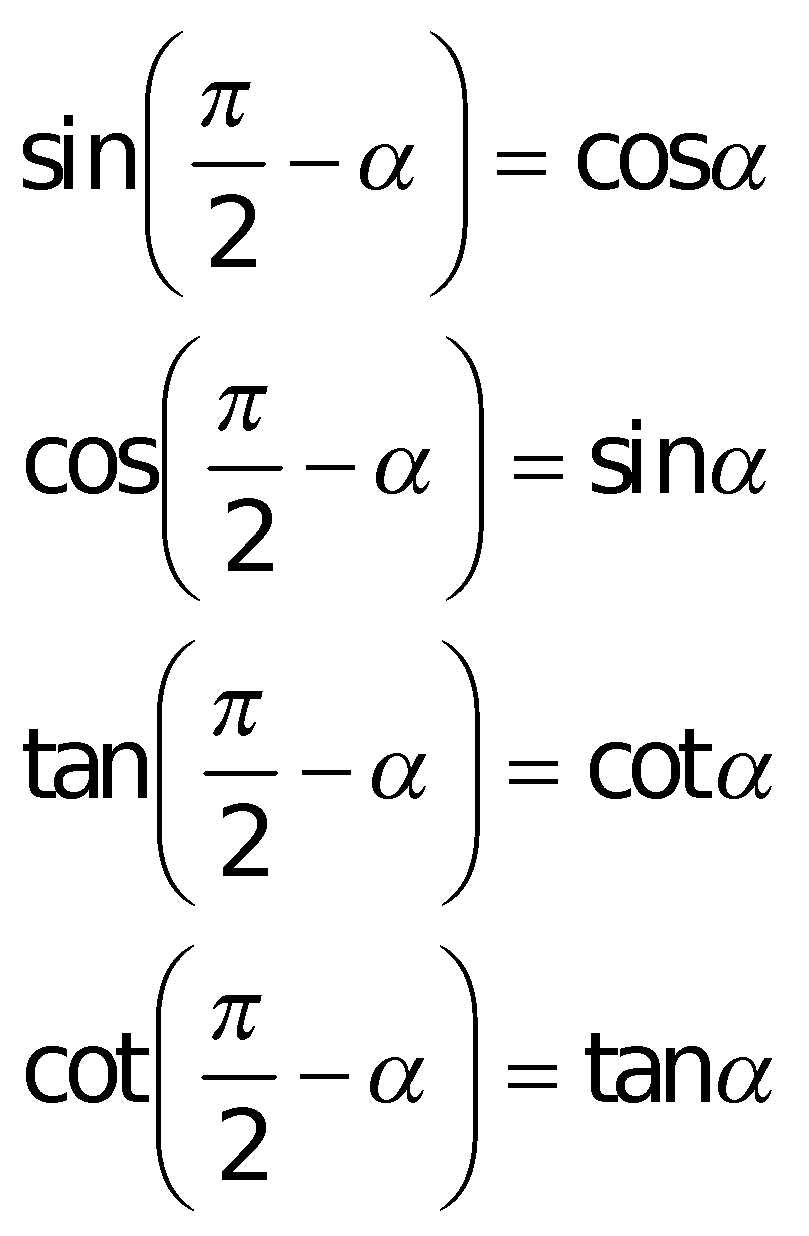


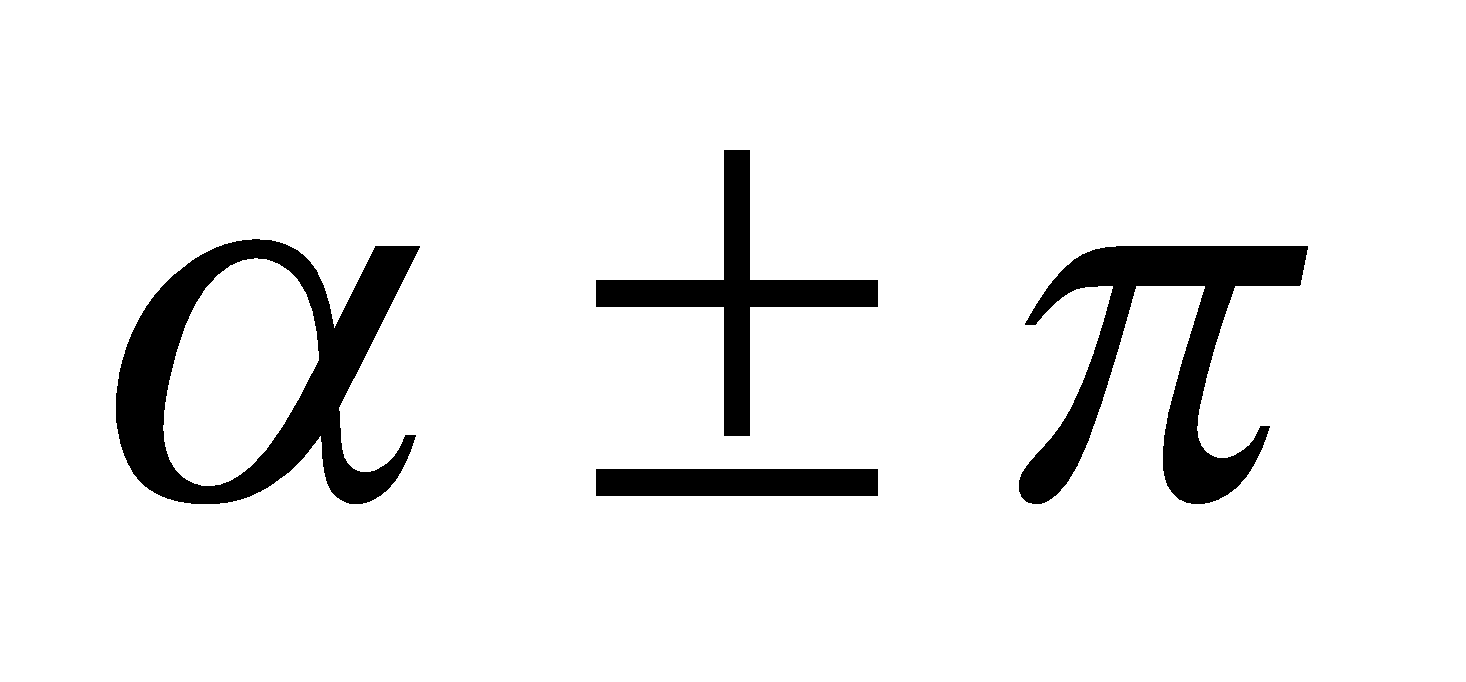
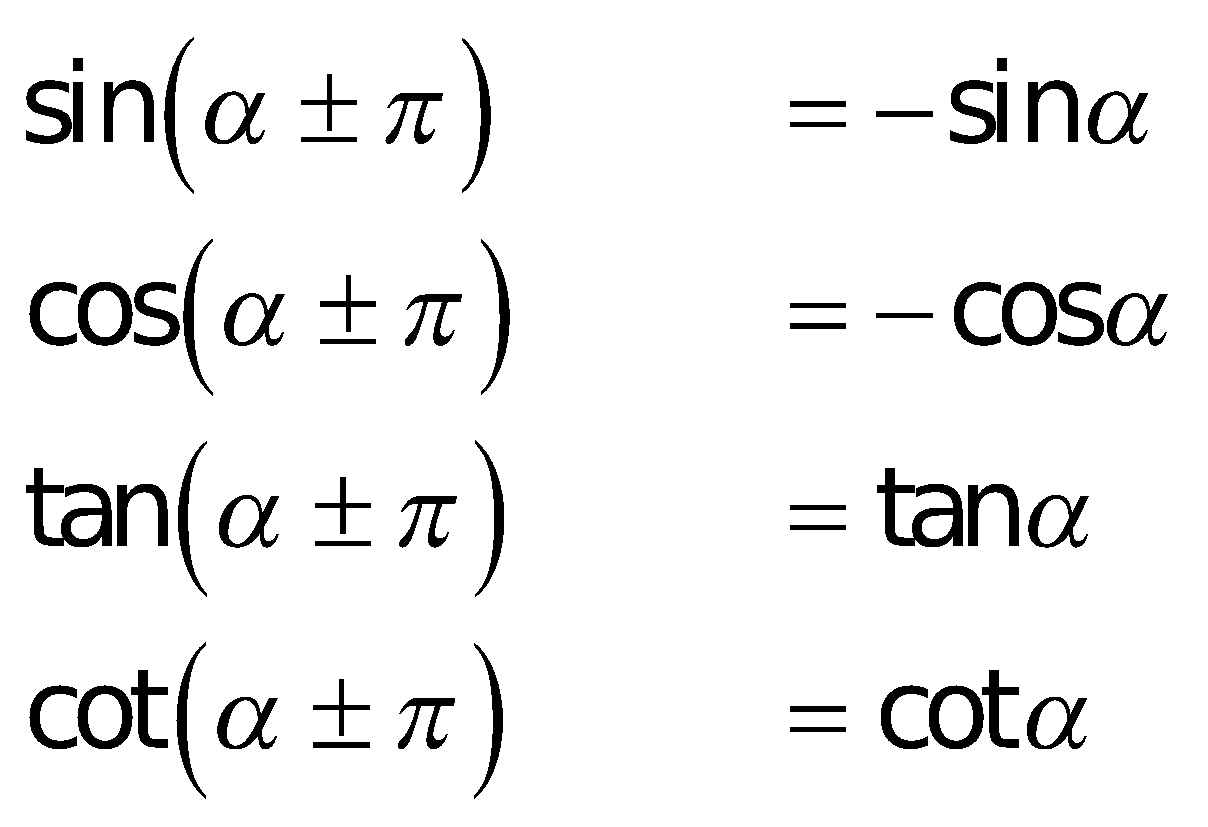

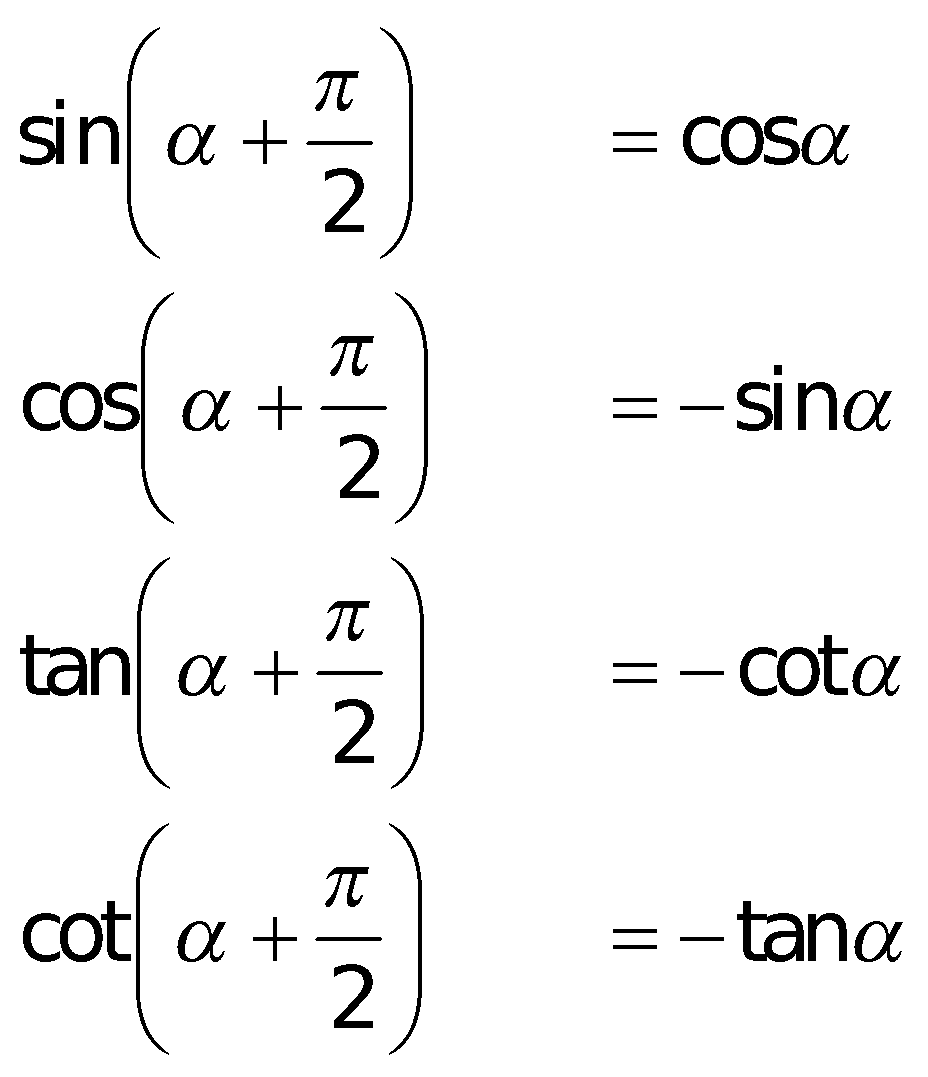
l. Bí quyết tính 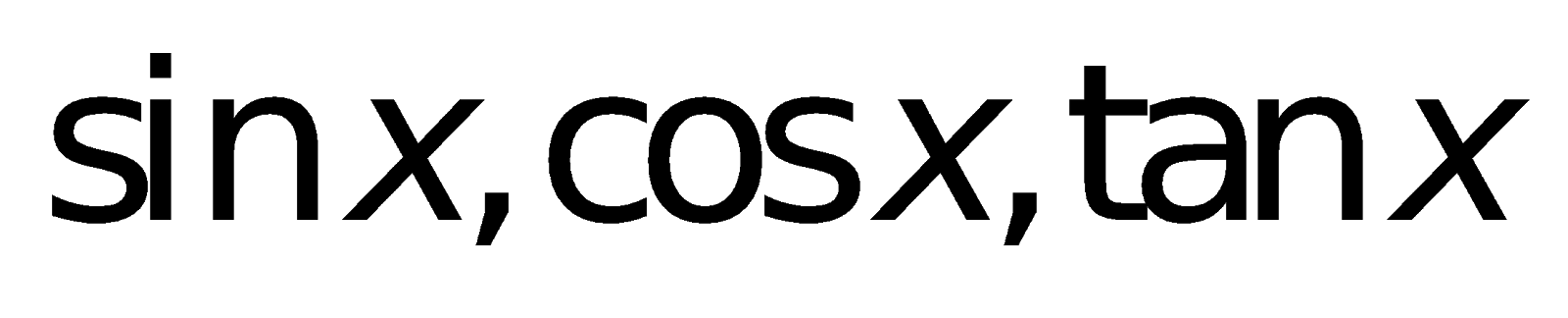
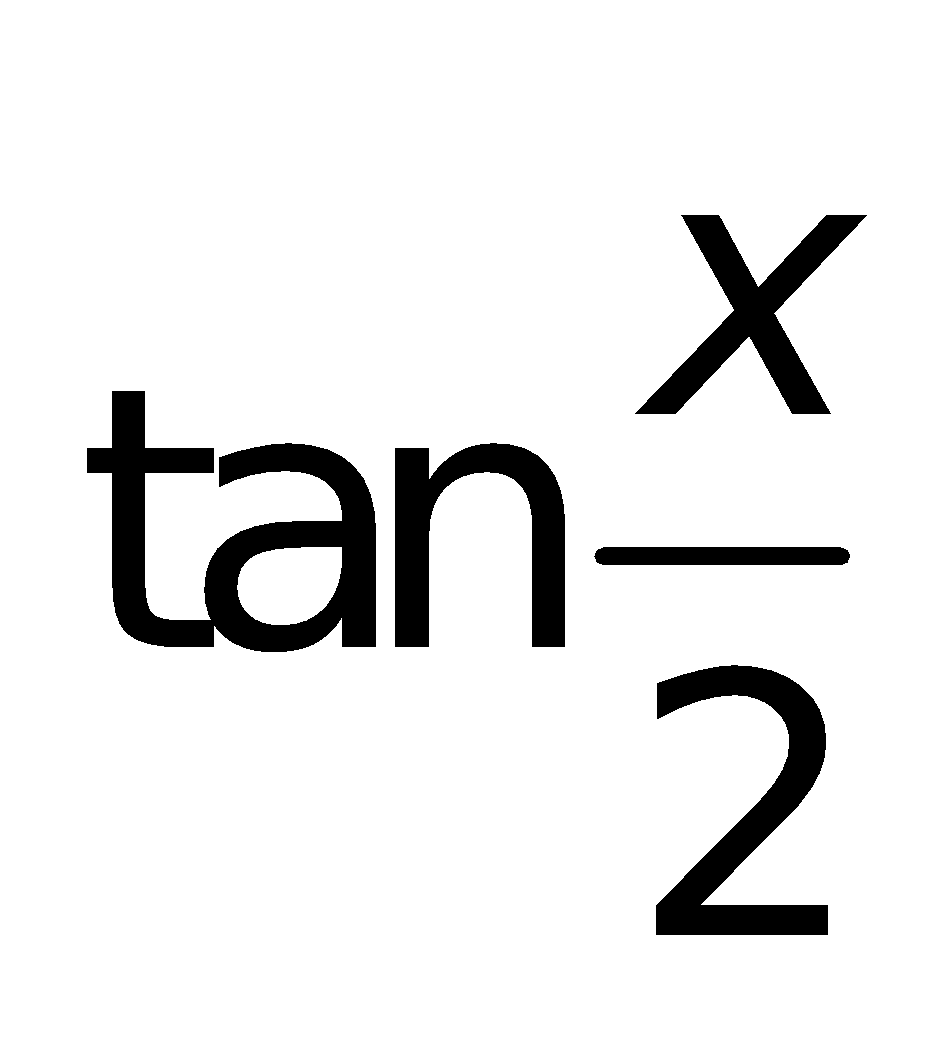
Nếu để
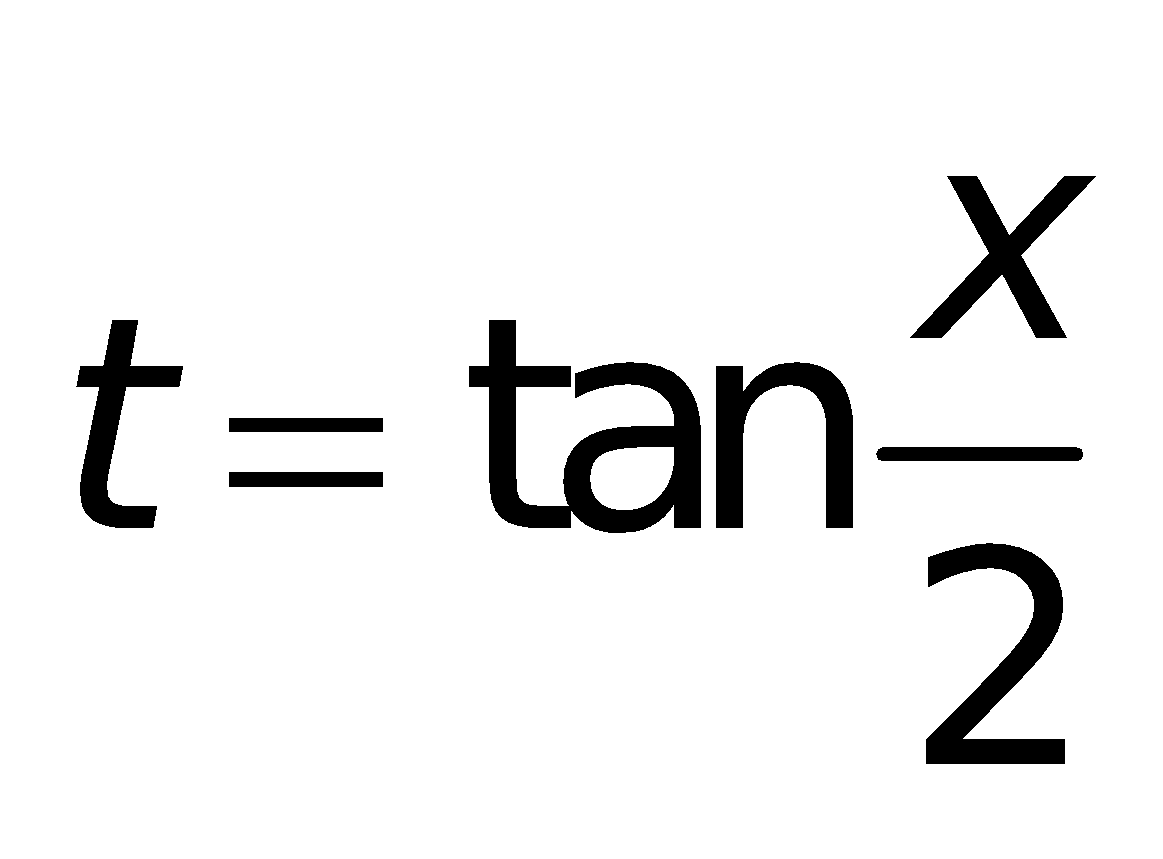
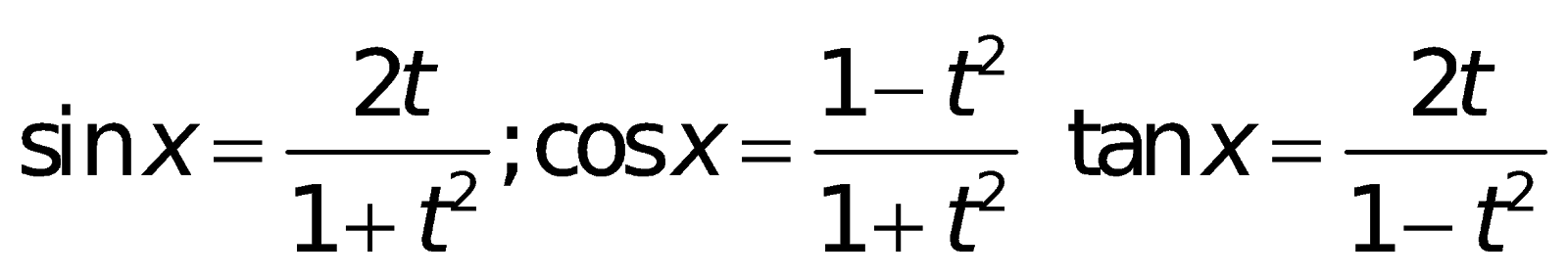
m. Một số công thức khác:
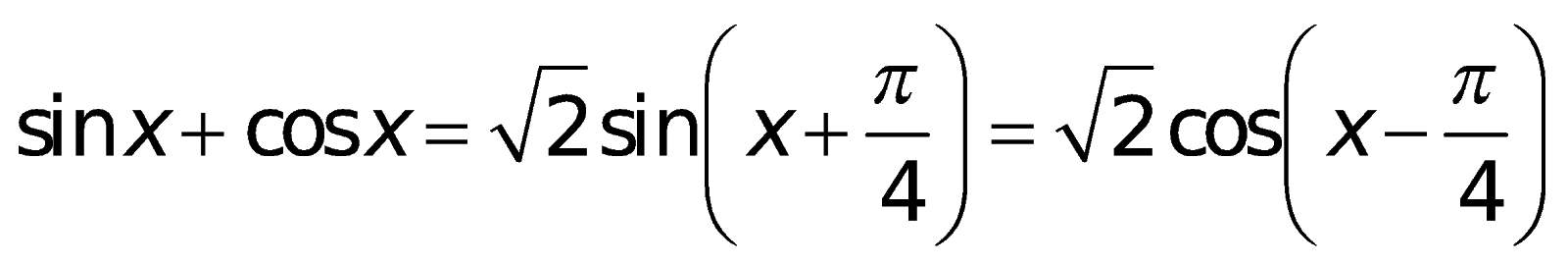
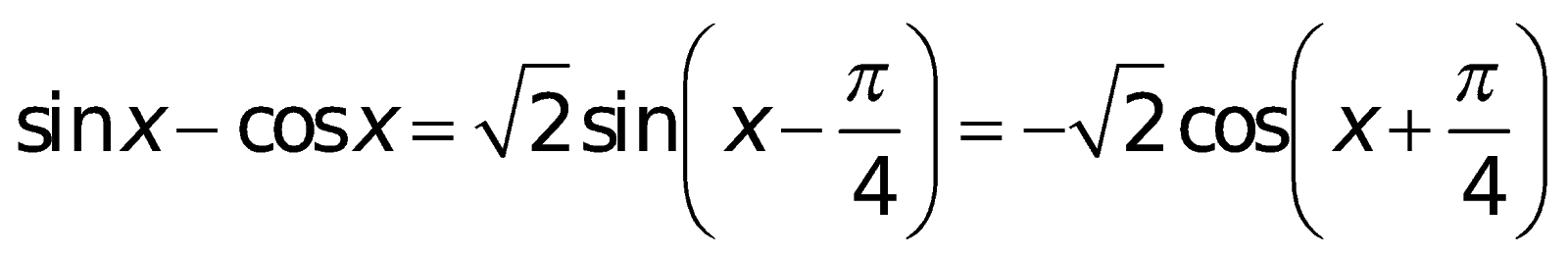
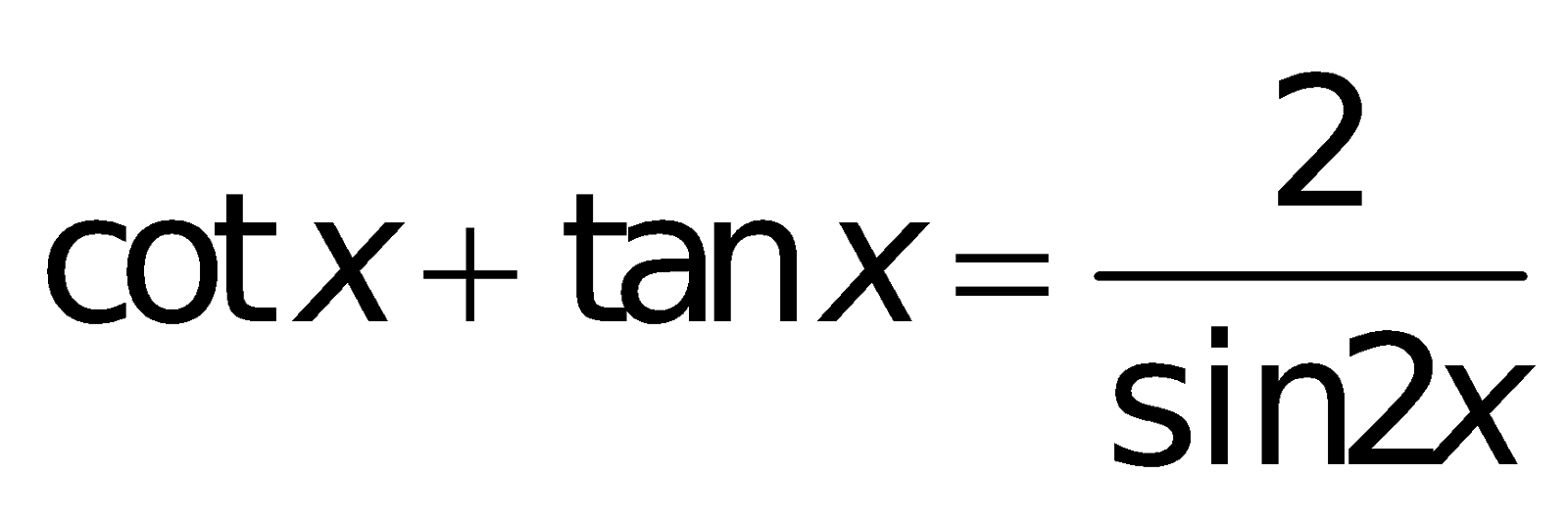
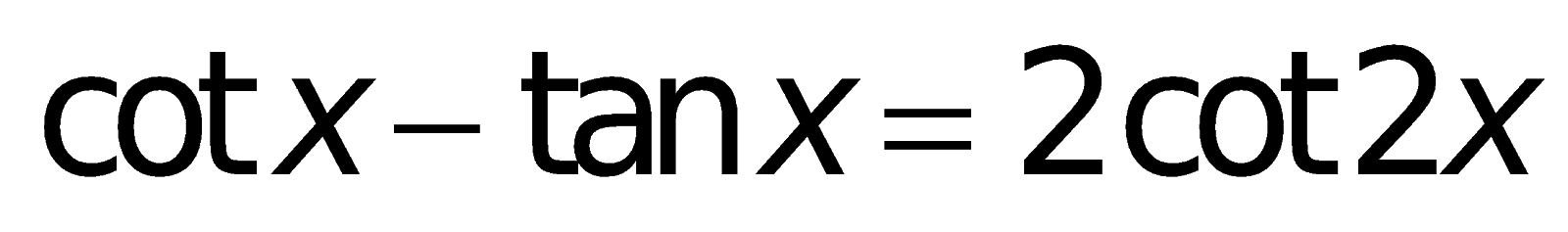
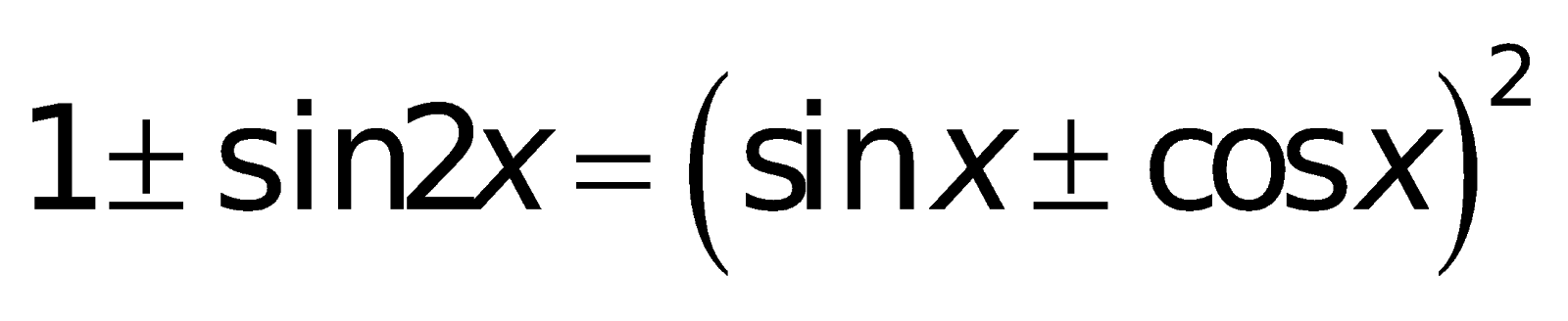
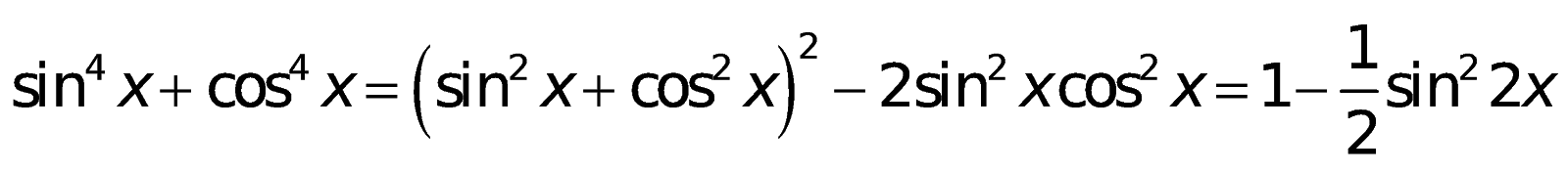
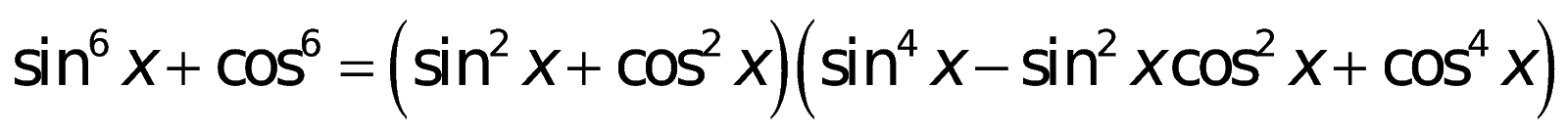
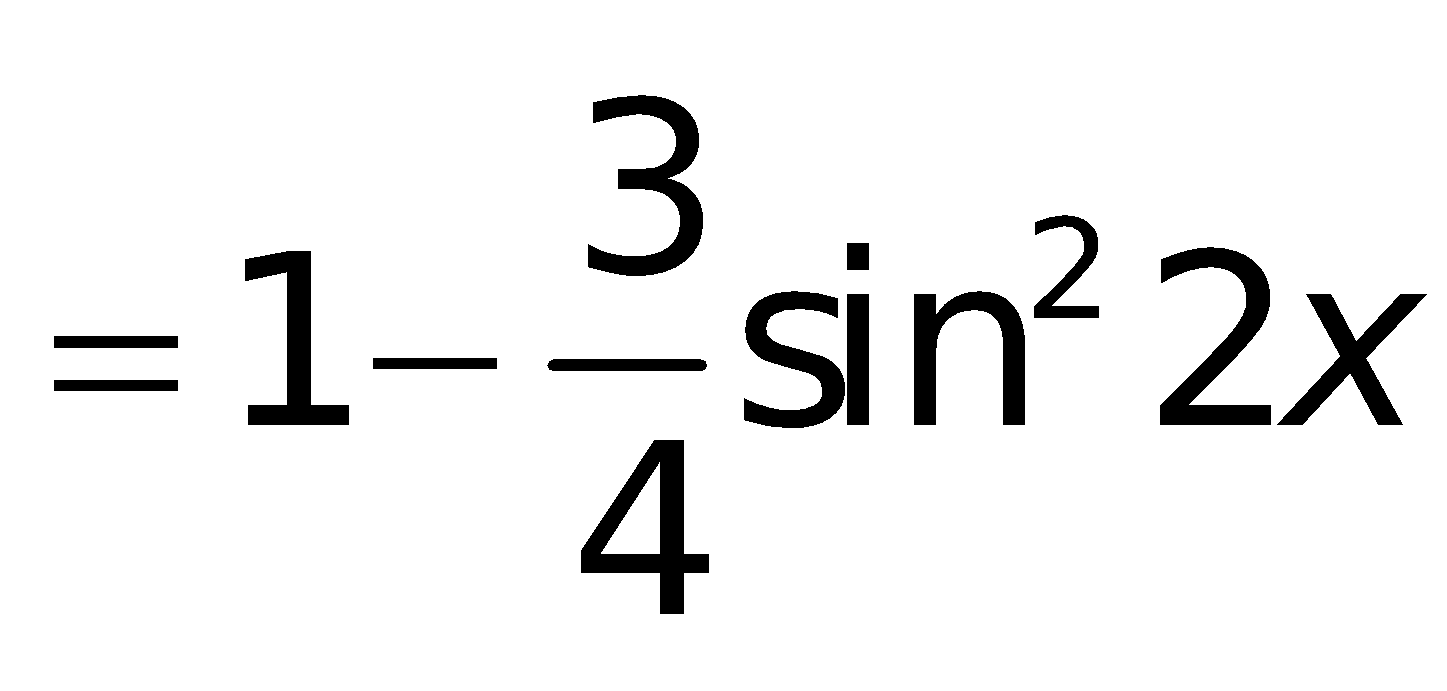
II. Phương pháp toán lớp 10 phần Hình học
1. Những công thức toán lớp 10 về hệ thức lượng vào tam giác:

Cho
Định lí côsin:
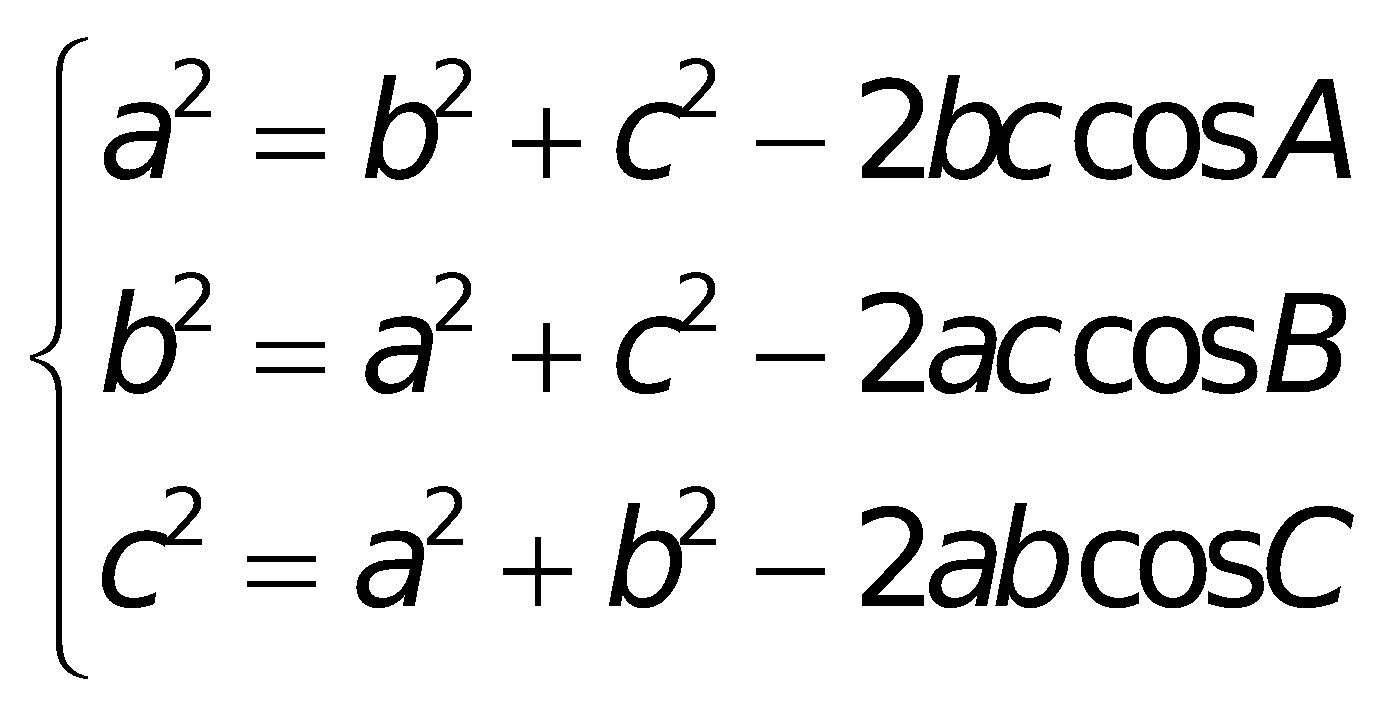
Định lí sin:
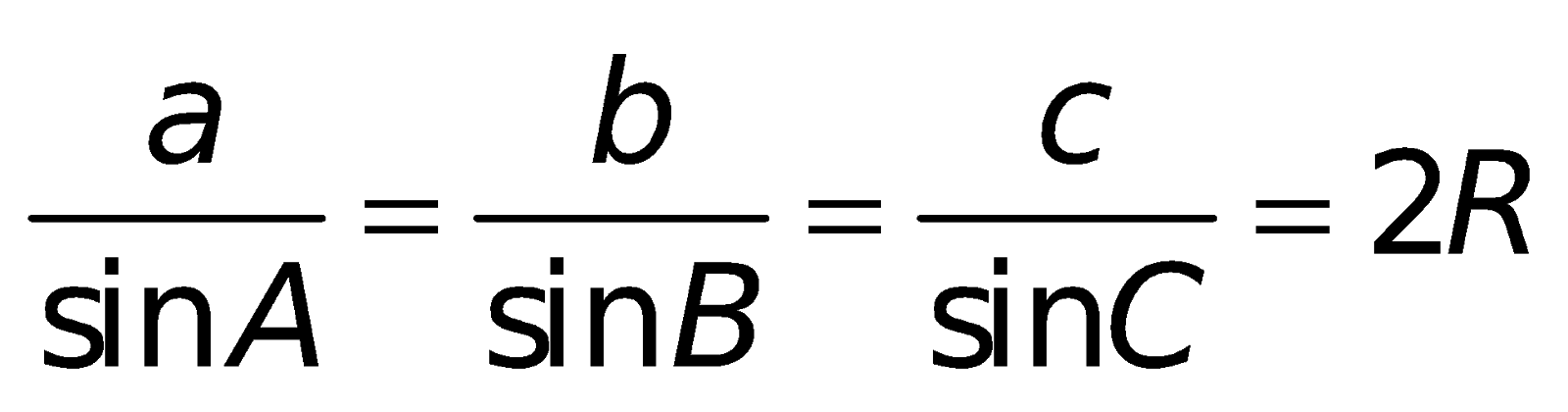
Công thức tính độ lâu năm trung tuyến:
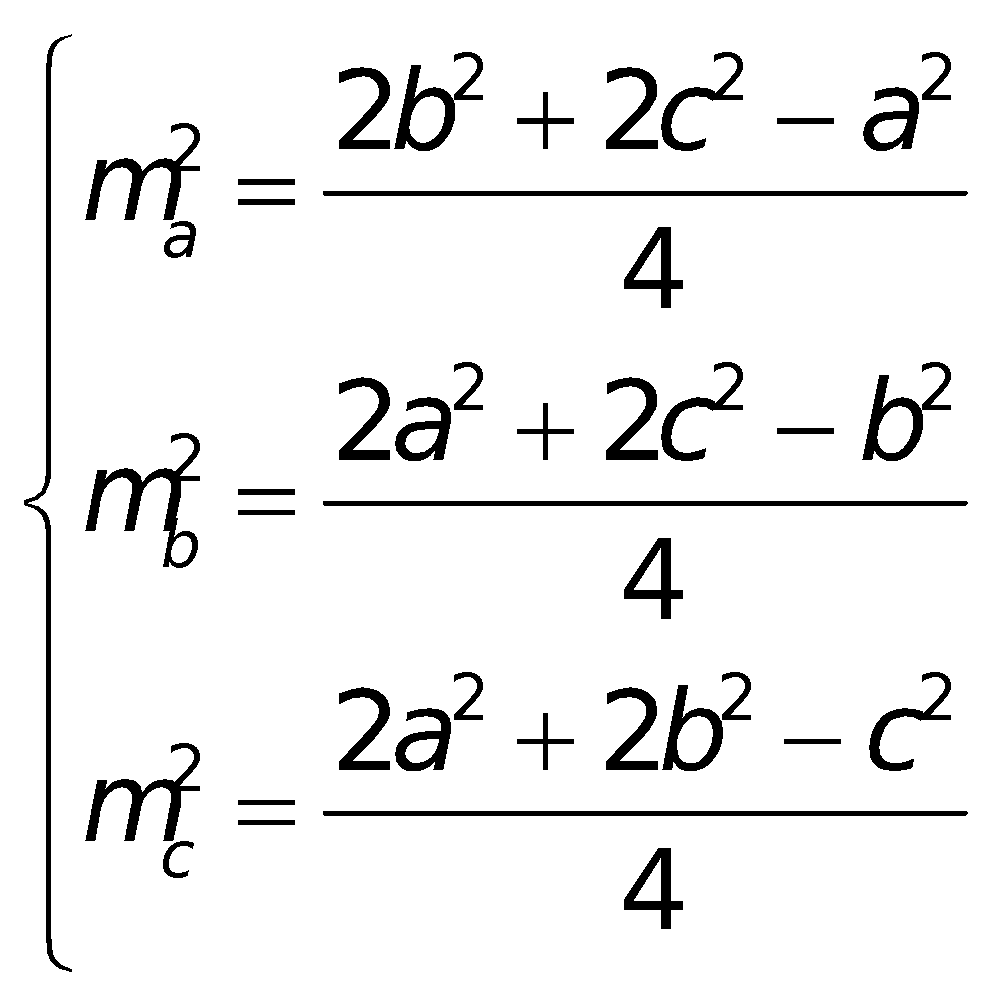
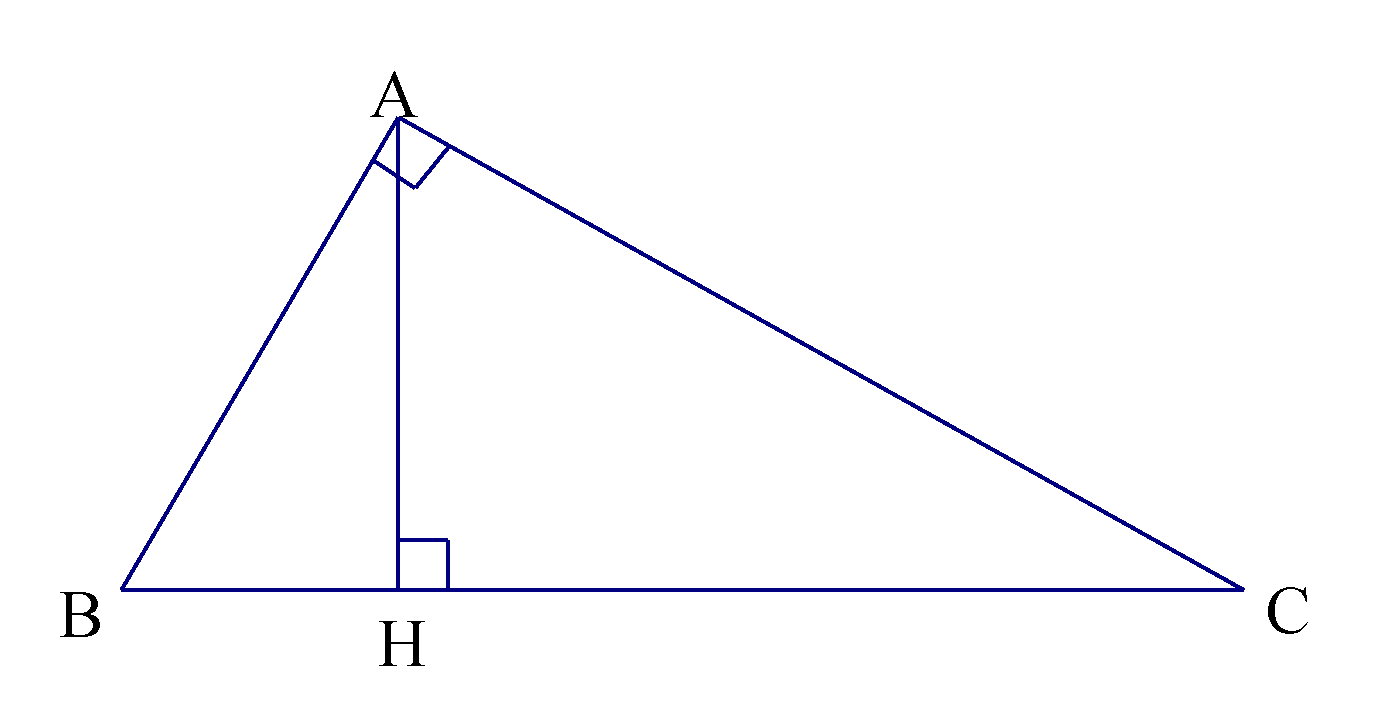
2. Các công thức toán lớp 10 về hệ thức lượng vào tam giác vuông
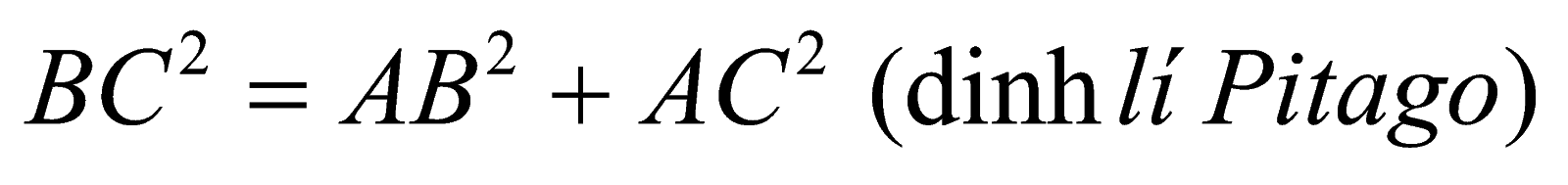

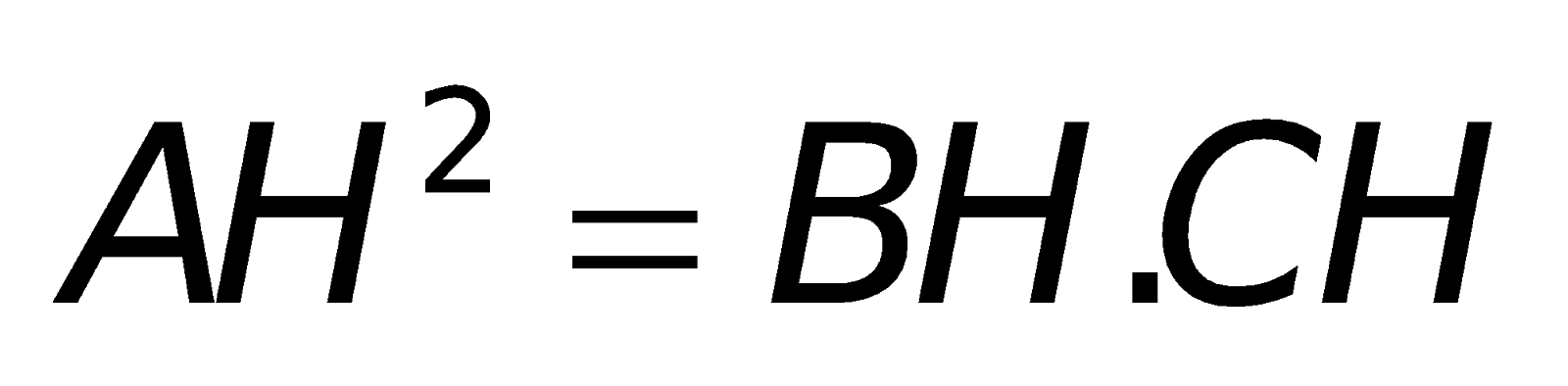
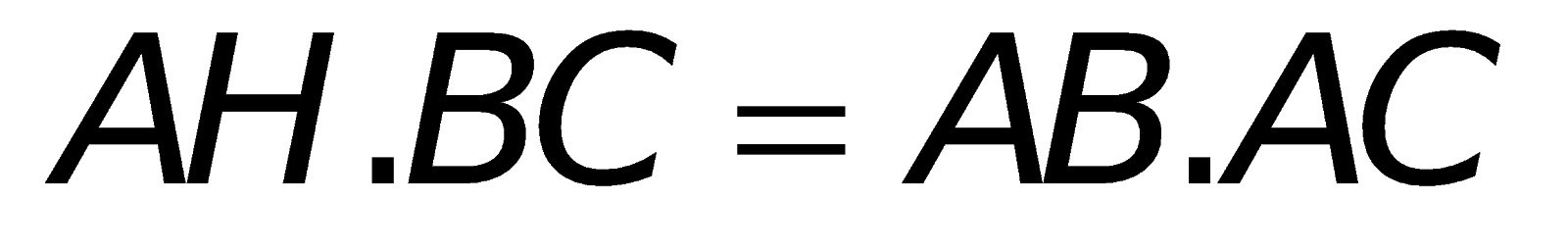
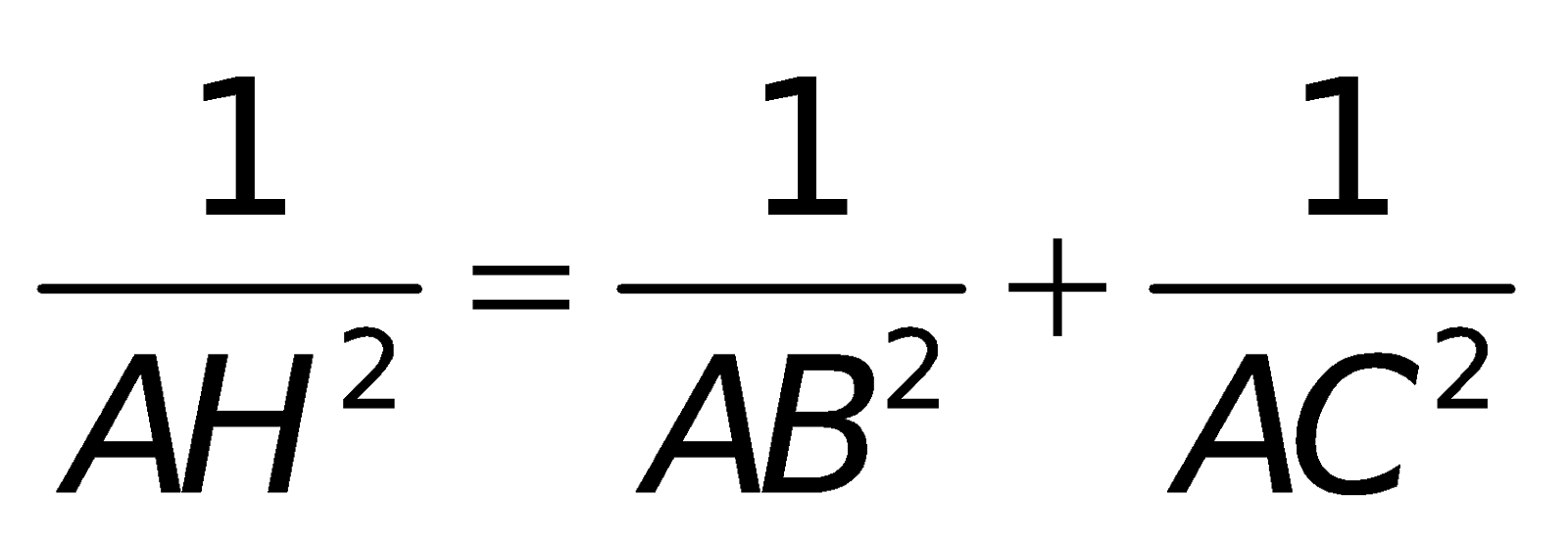
3. Các công thức tính diện tích:
Tam giác thường:
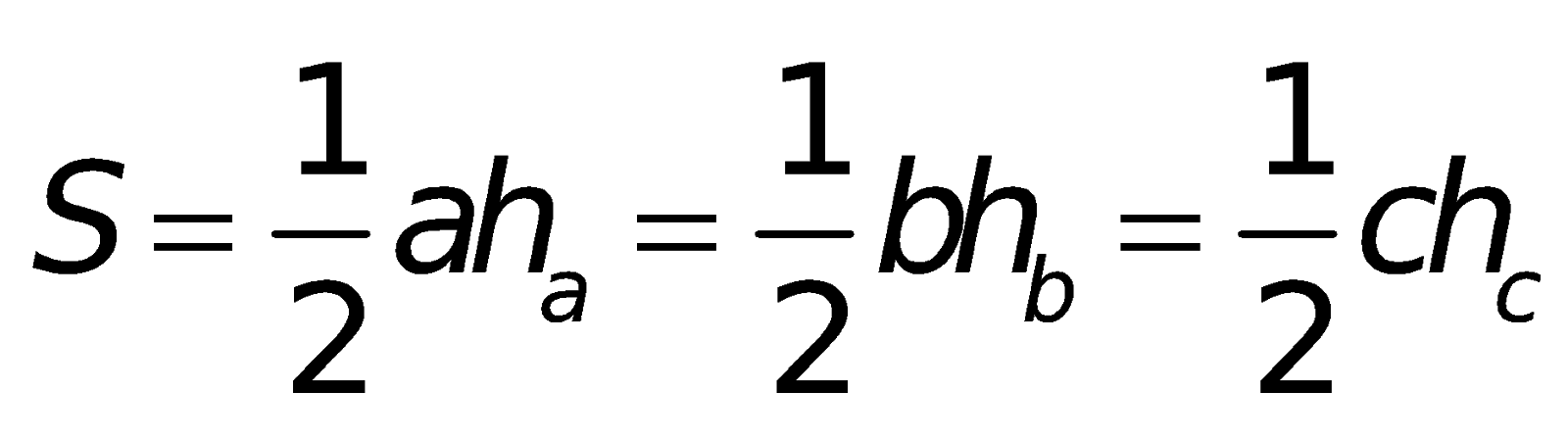
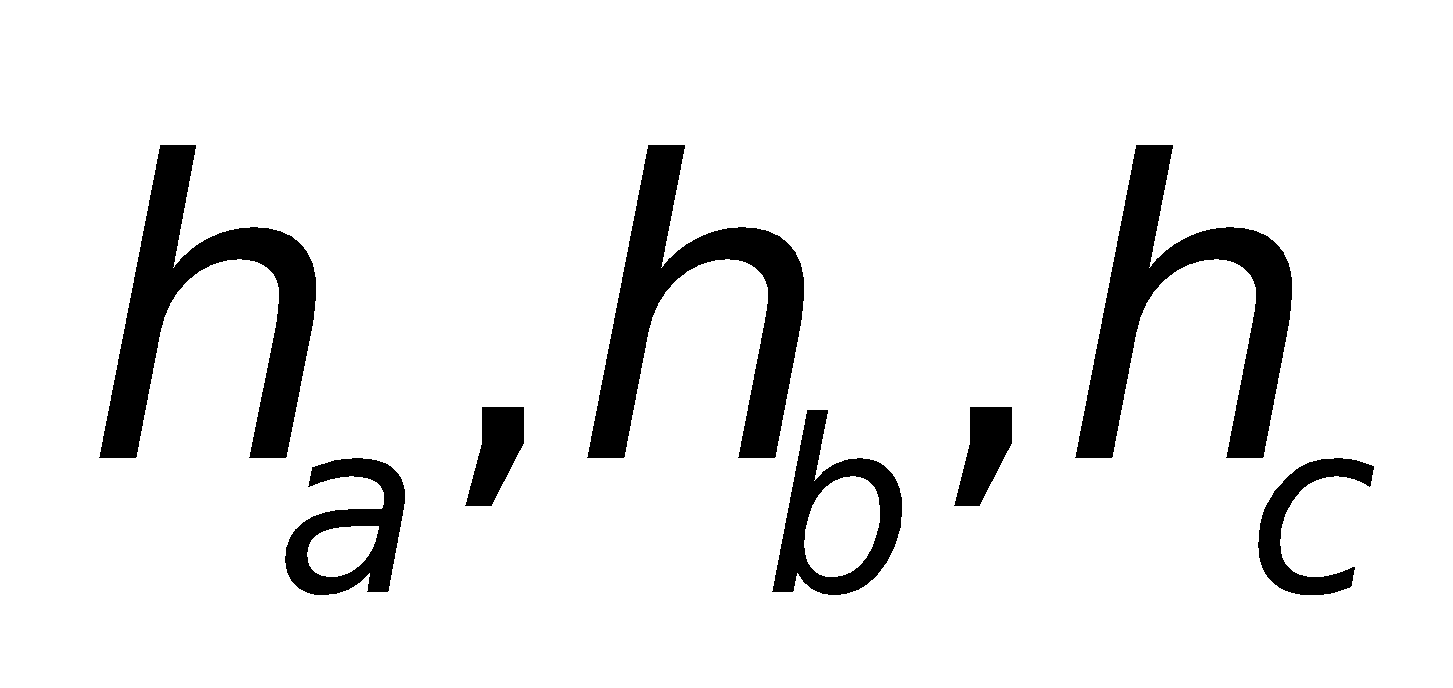
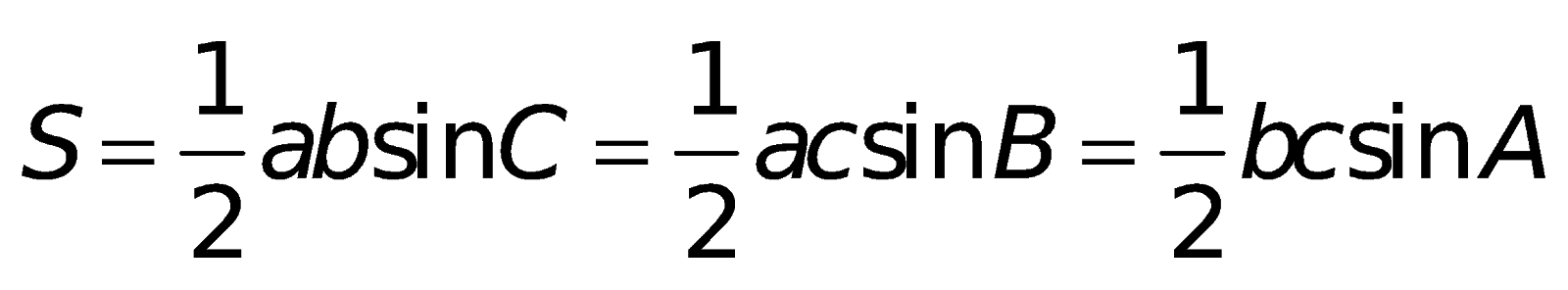
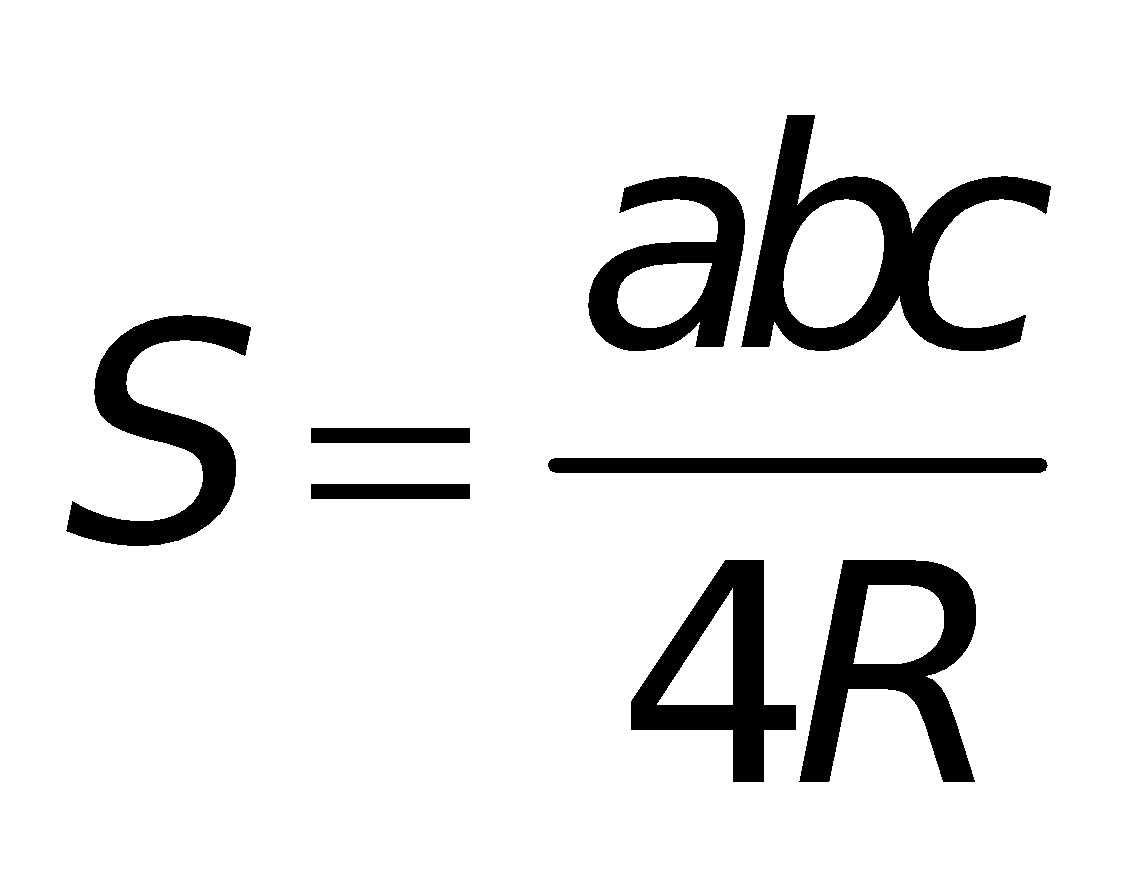
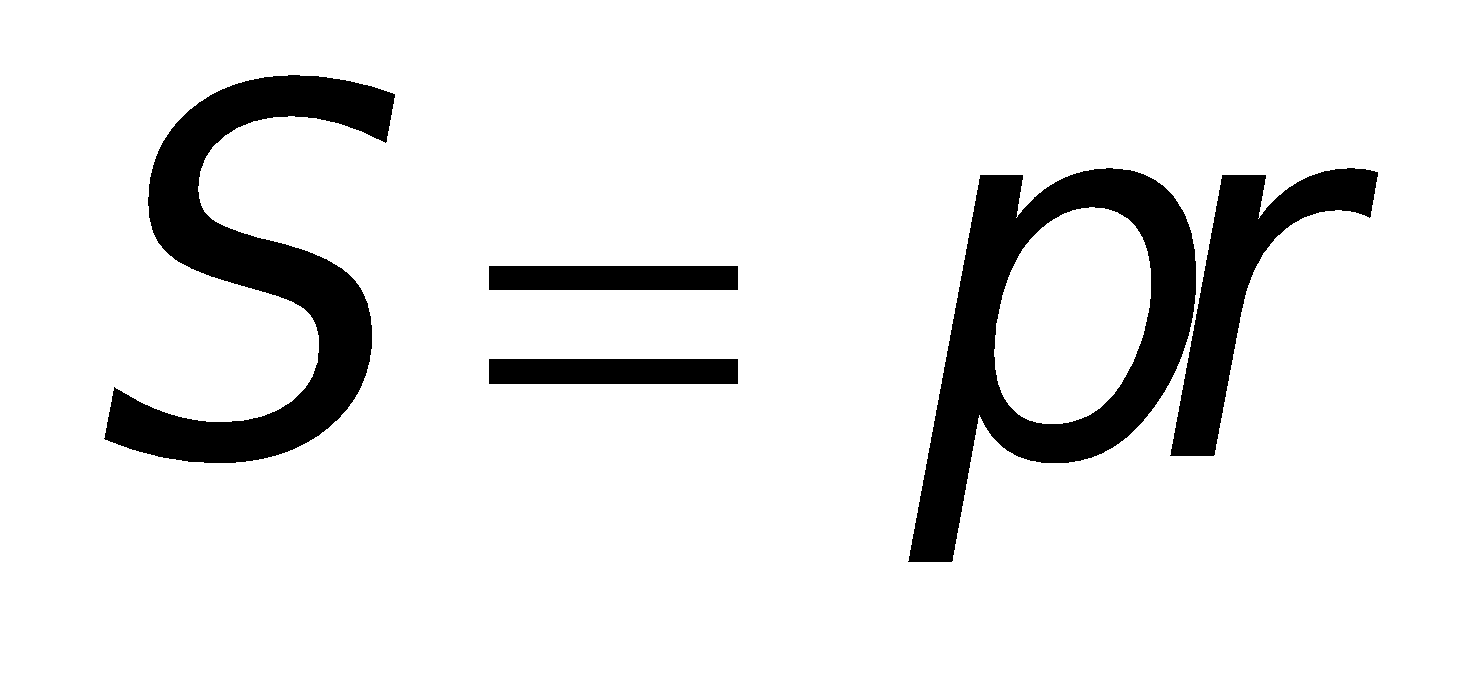
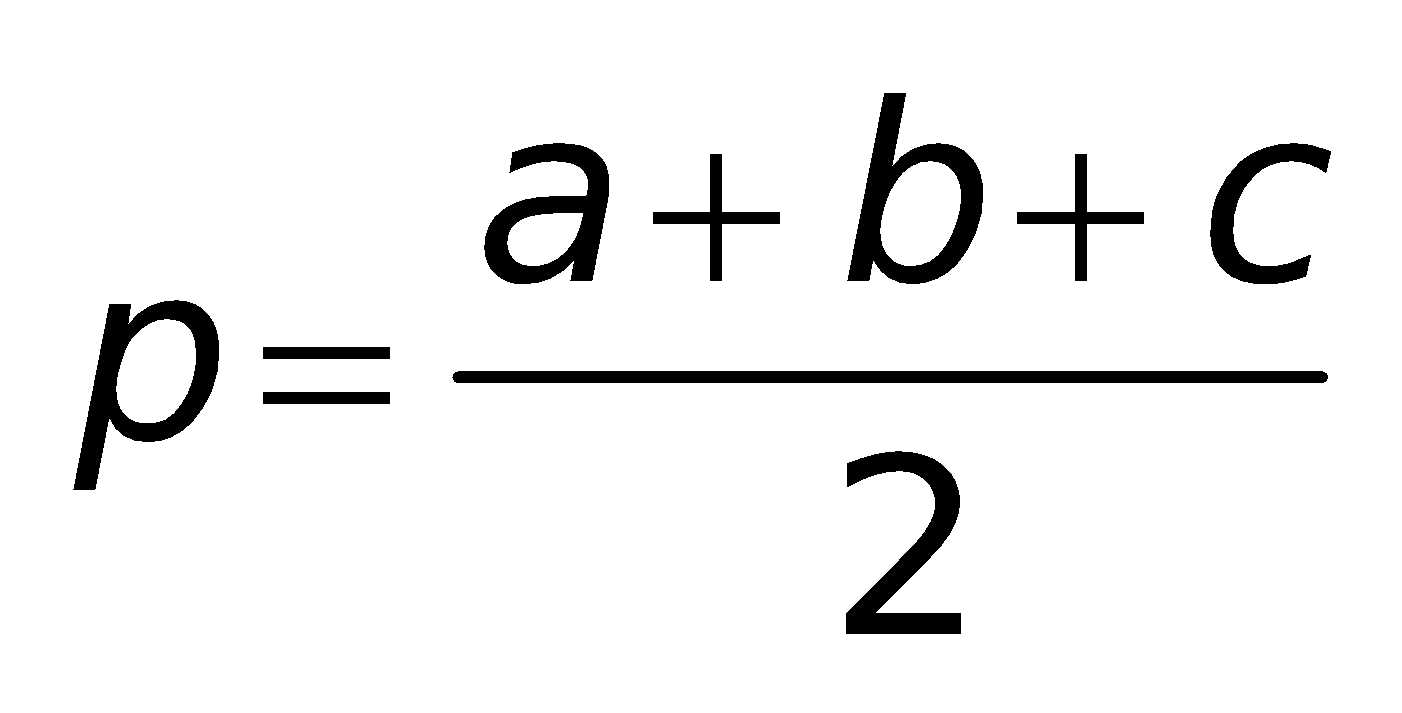
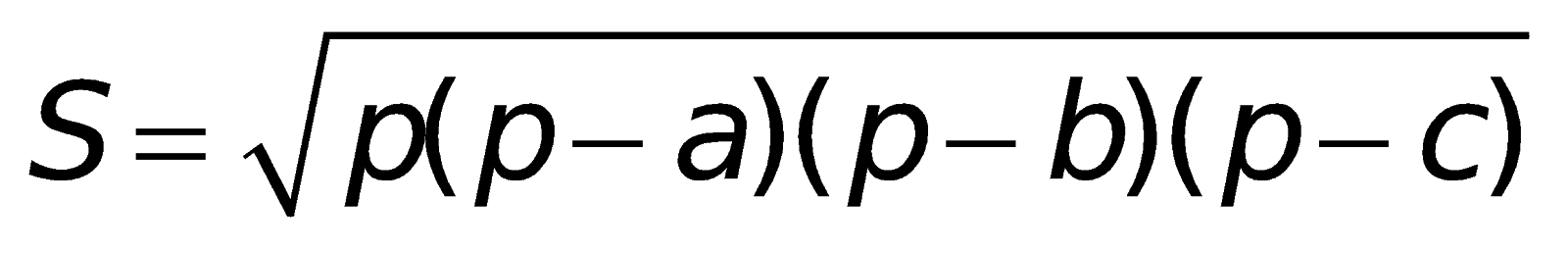
Tam giác vuông:
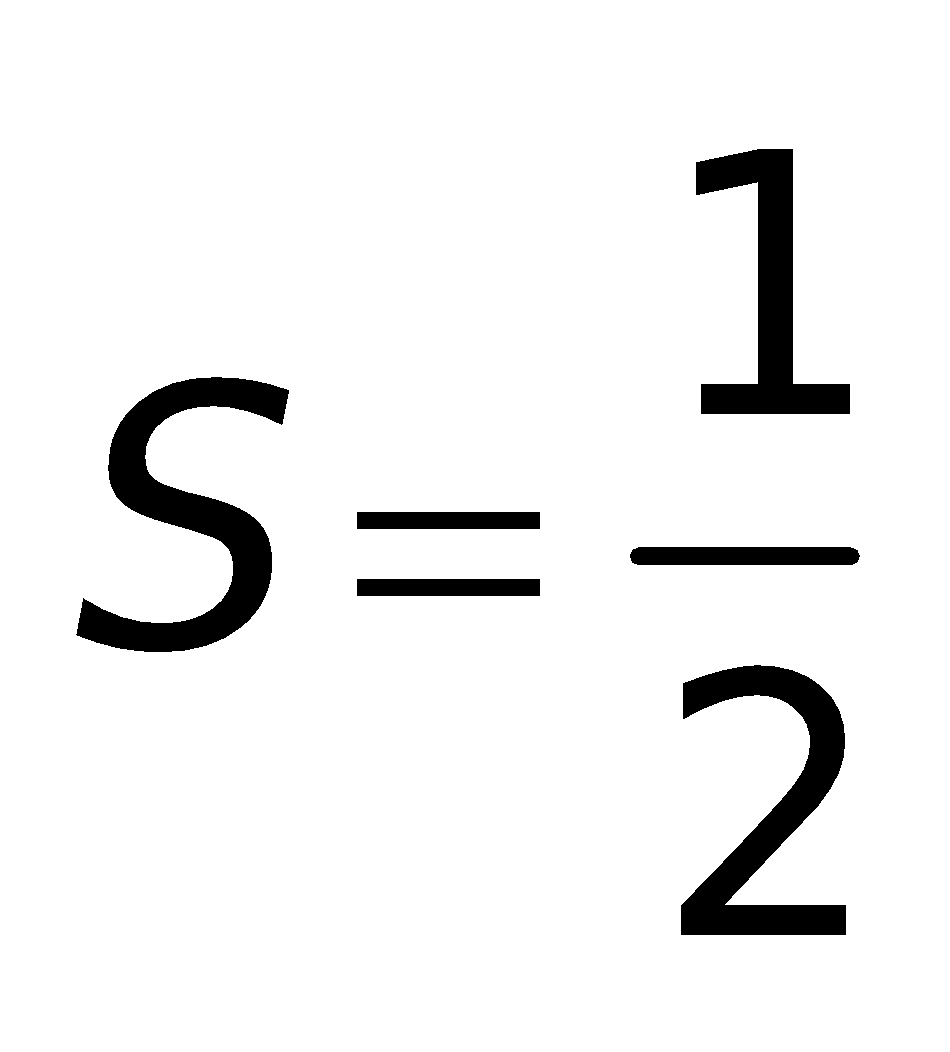
Tam giác gần như cạnh a:
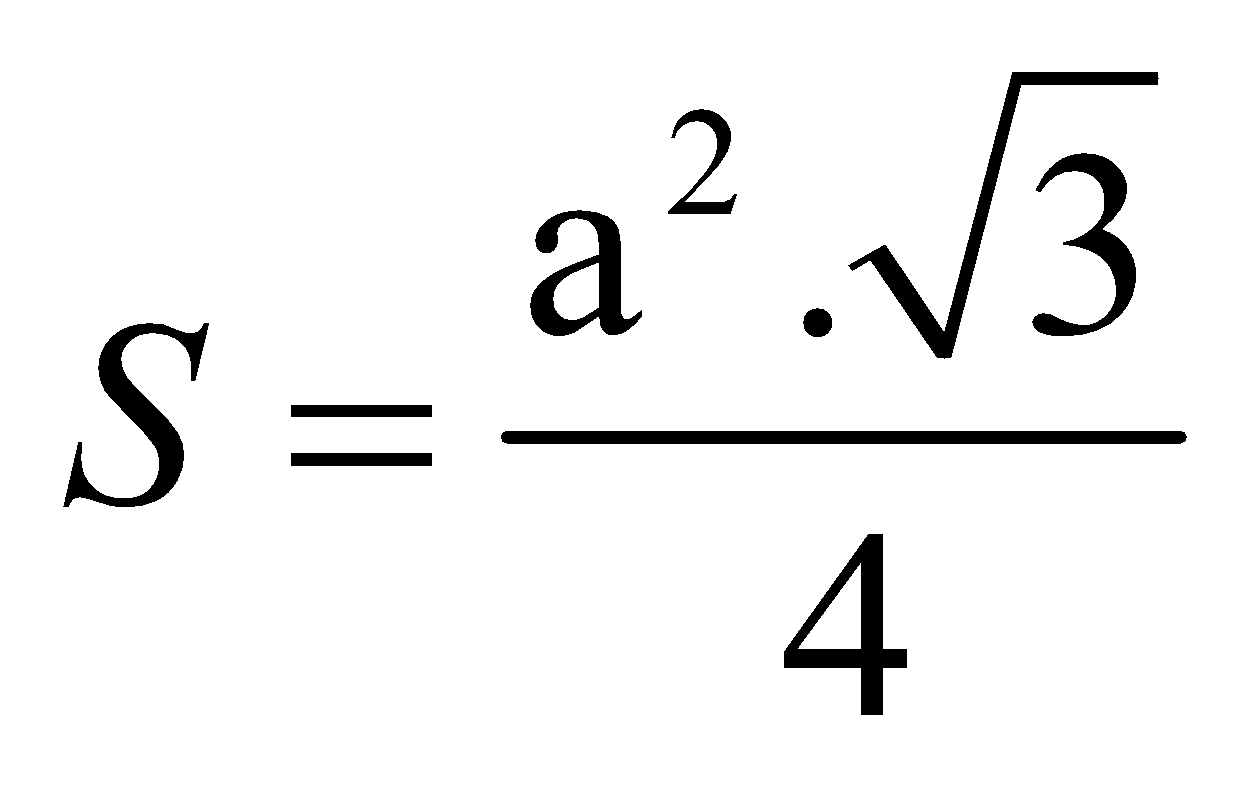
Hình vuông cạnh a:
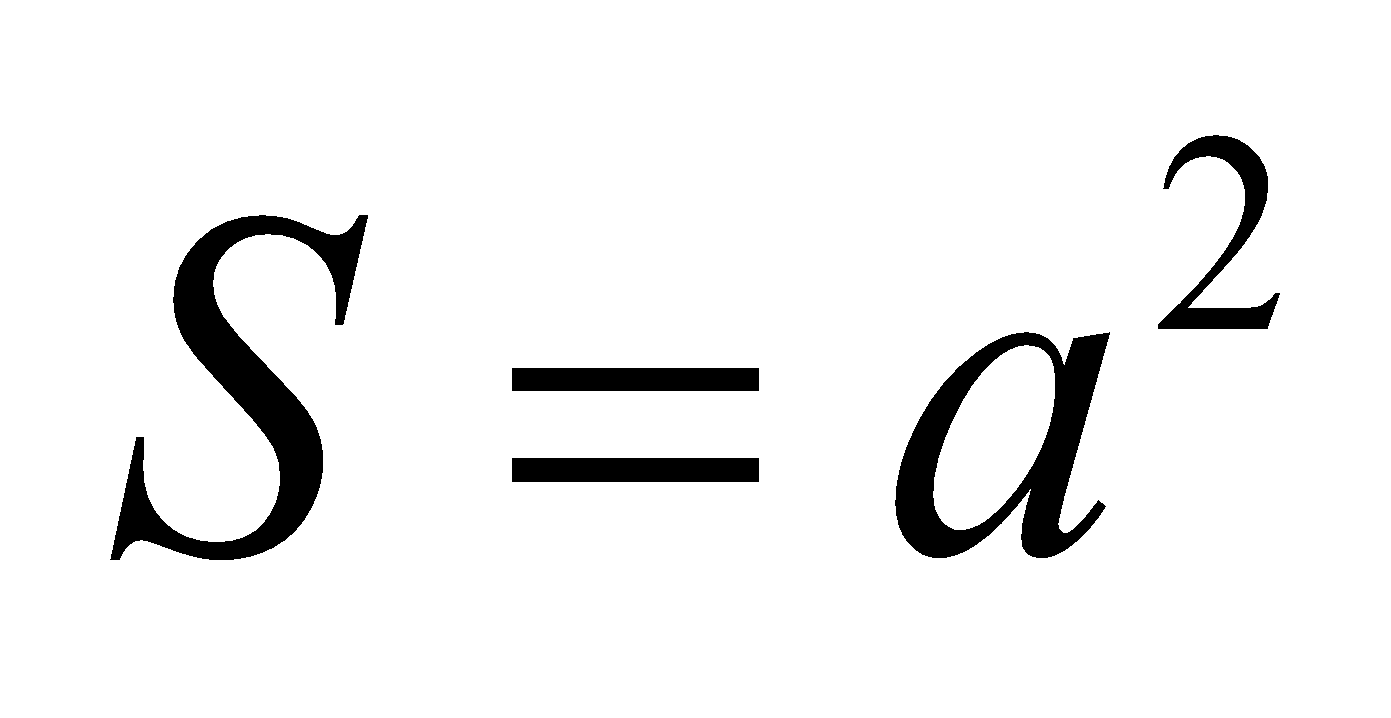
Hình chữ nhật:
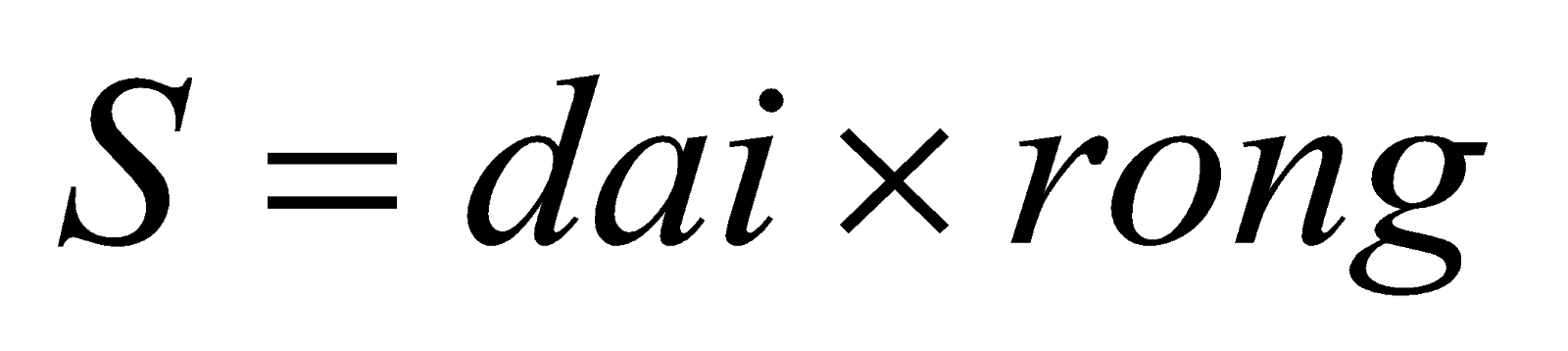
Hình bình hành:
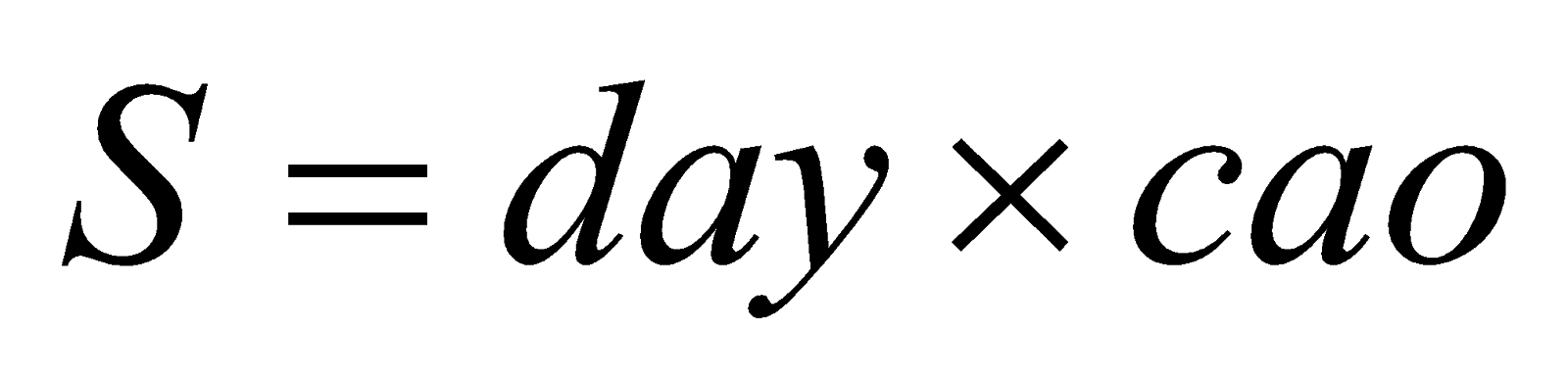

Hình thoi:
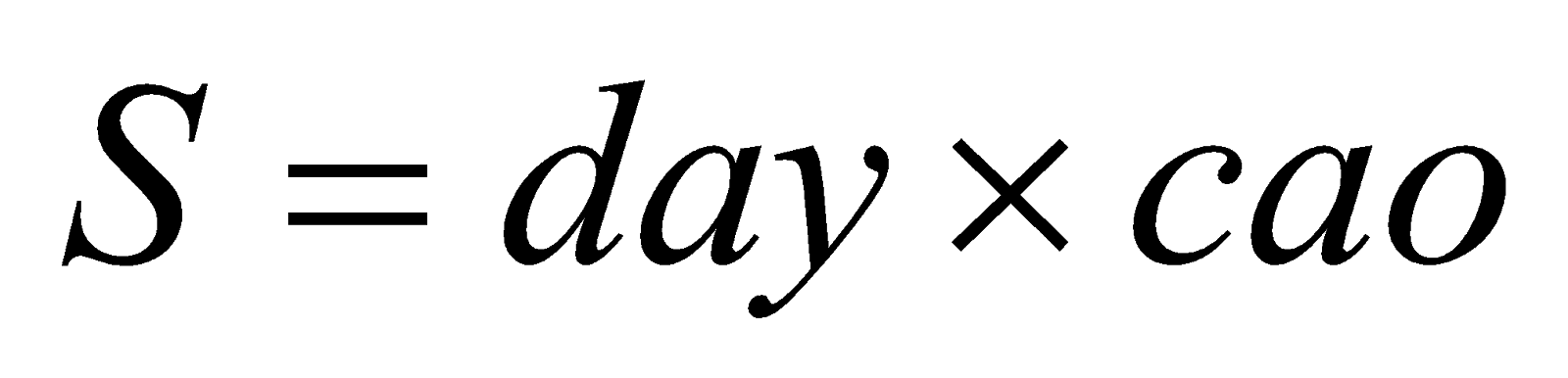

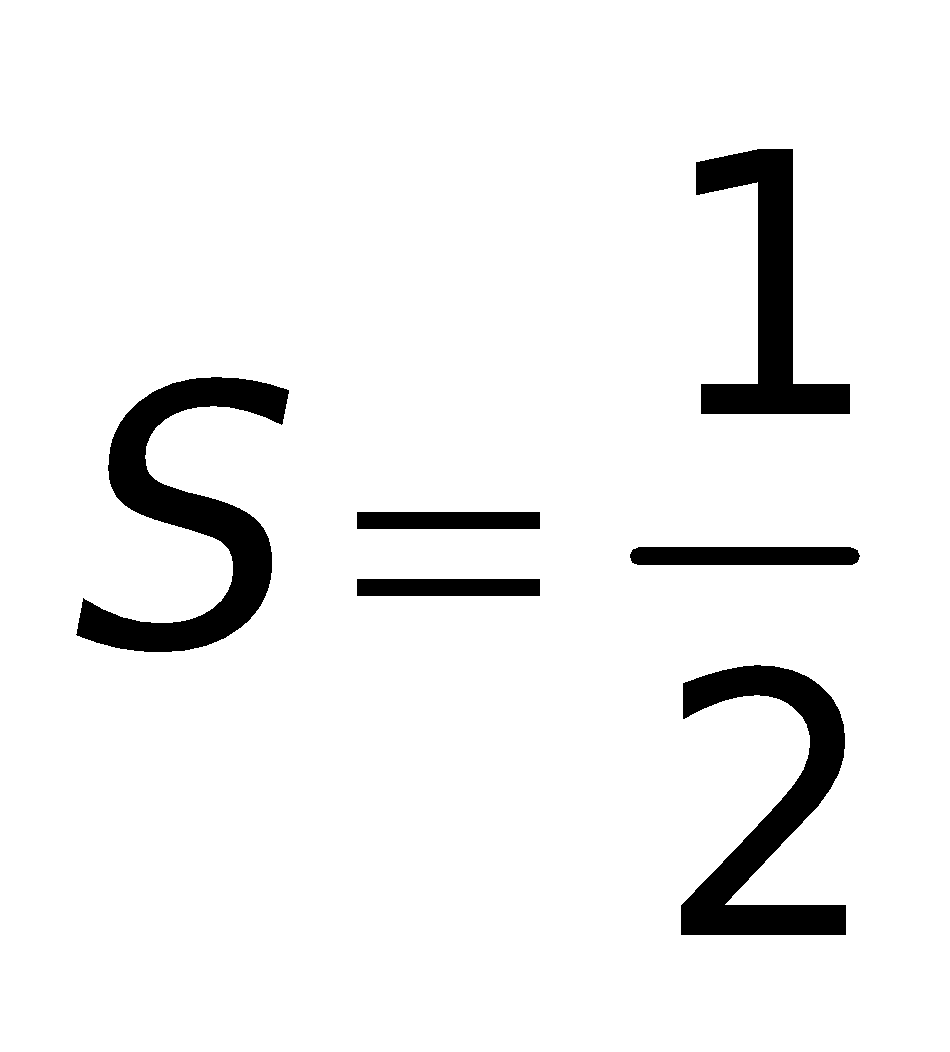
Hình tròn:
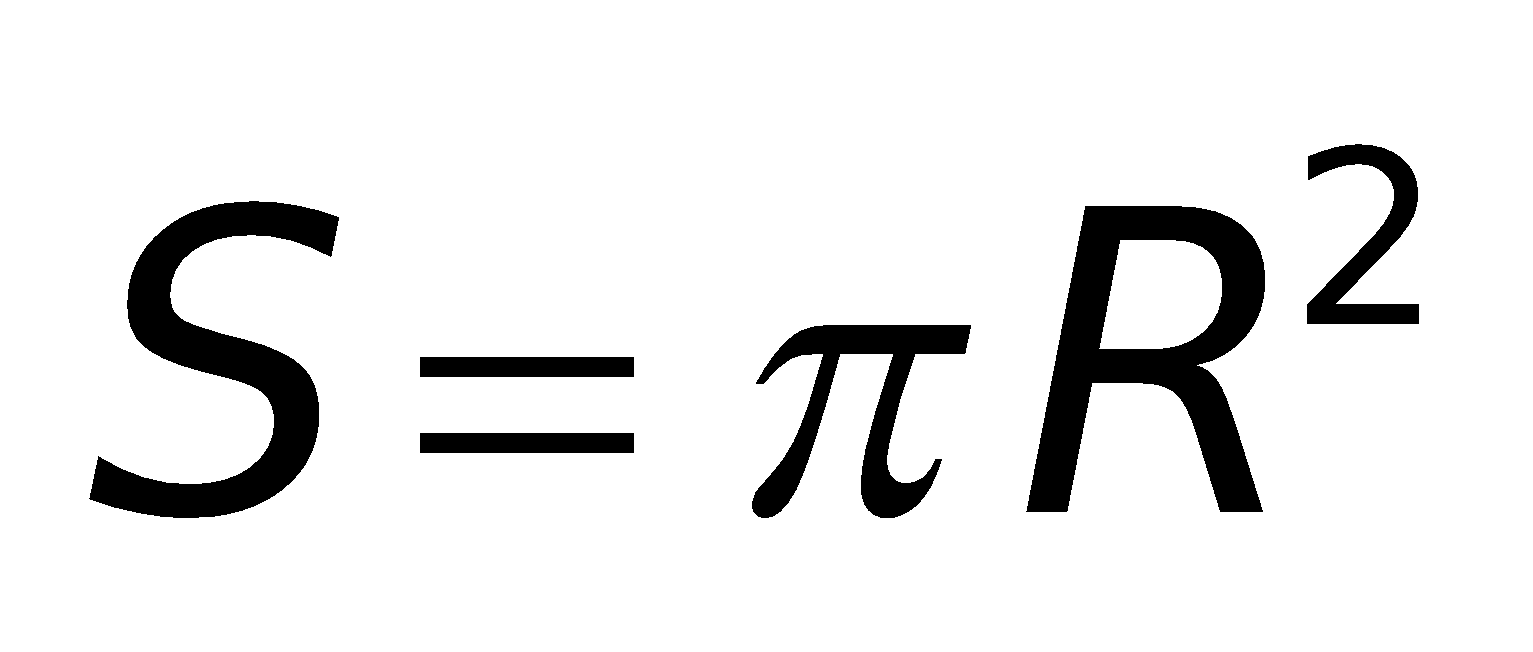
4. Phương pháp toán 10 về phương pháp tọa độ trong khía cạnh phẳng Oxy
Cho ba điểm:
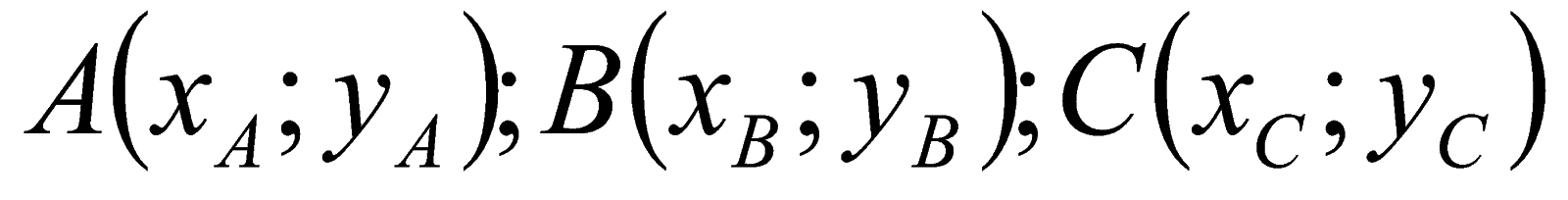
- Tọa độ véctơ
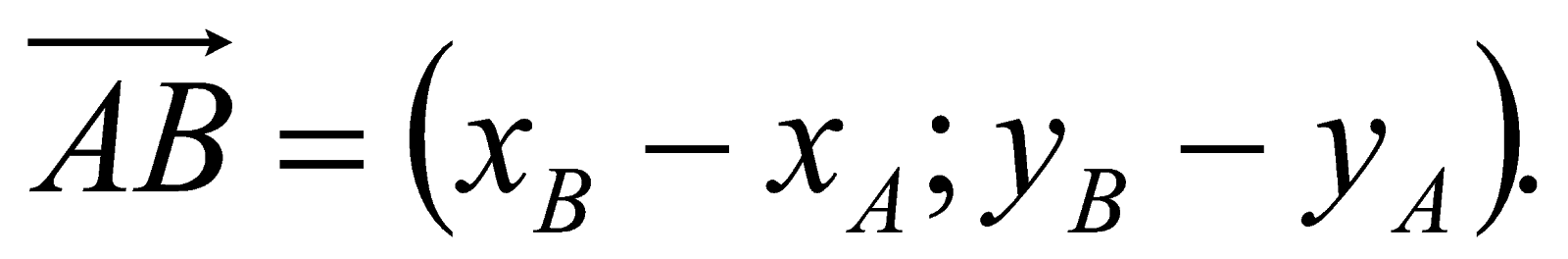
- Tọa độ trung điểm I của AB là:
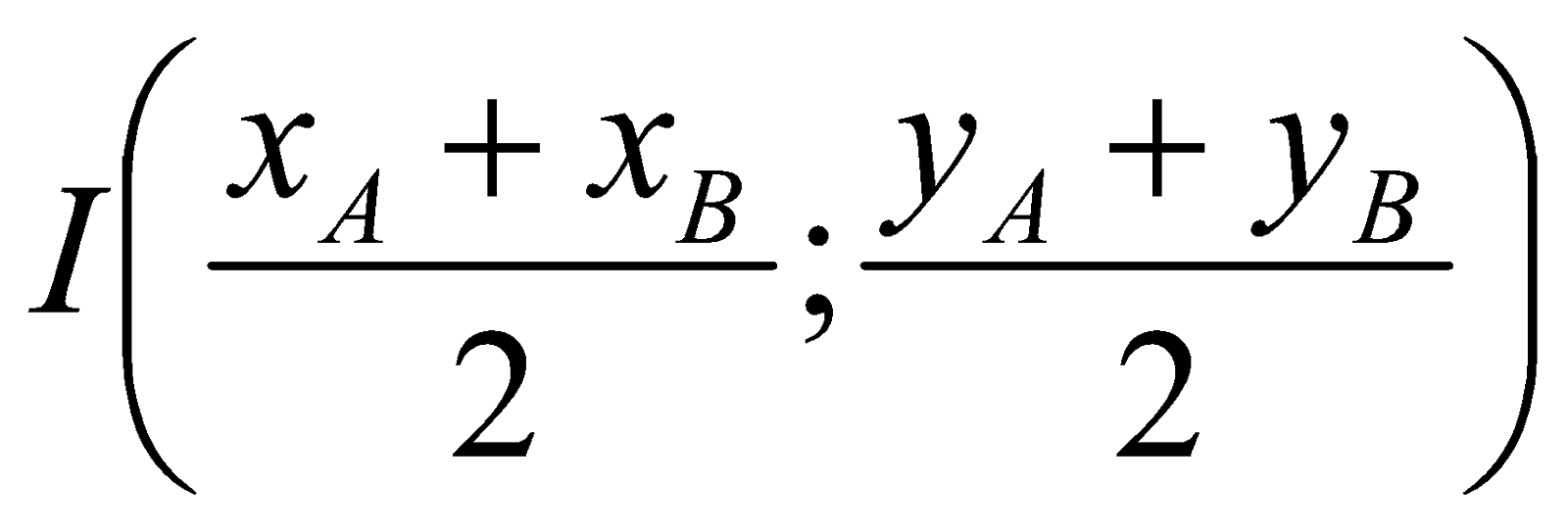

- Tọa độ trọng tâm G của
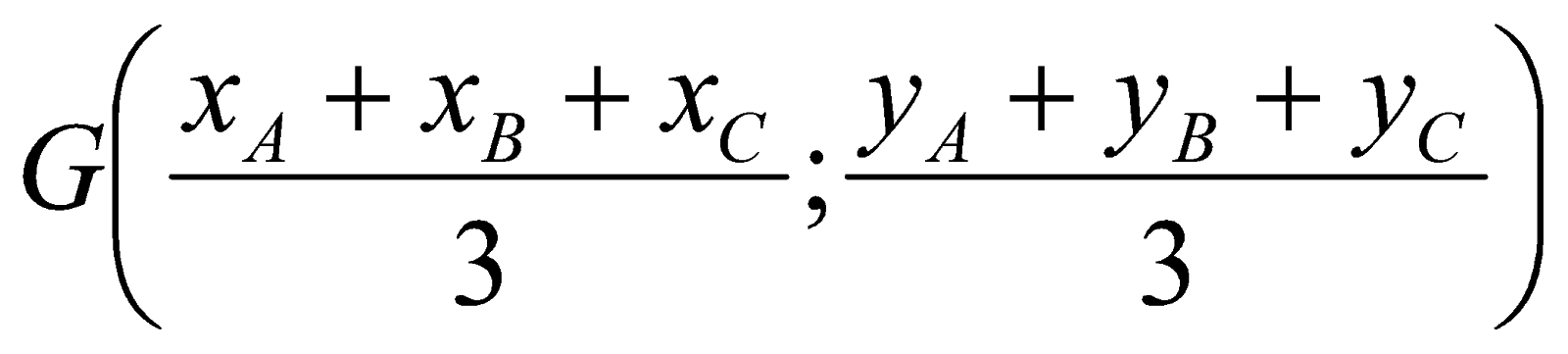
Cho các vec-tơ
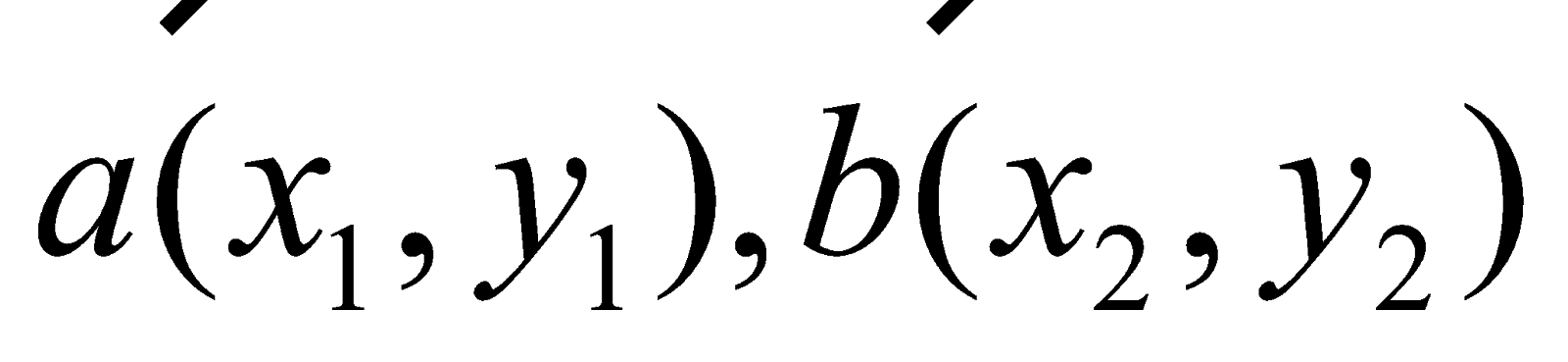
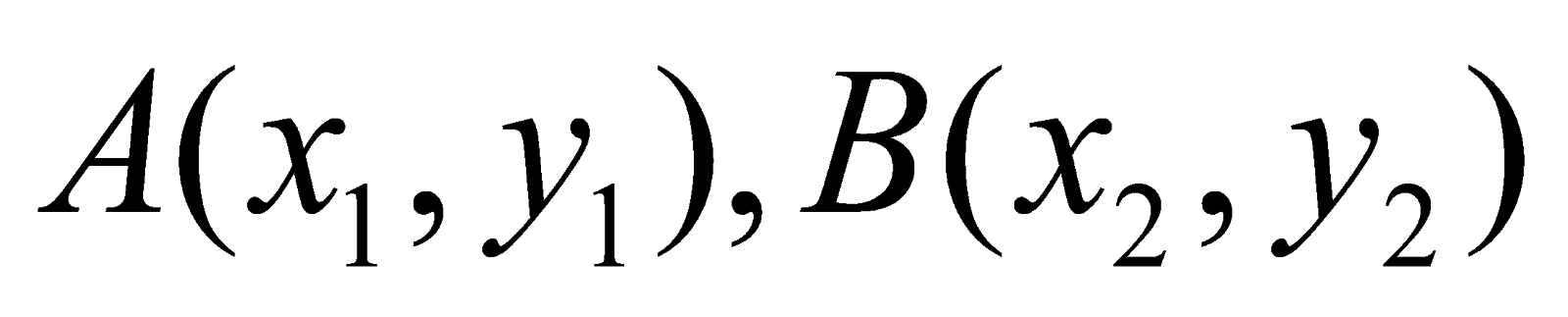
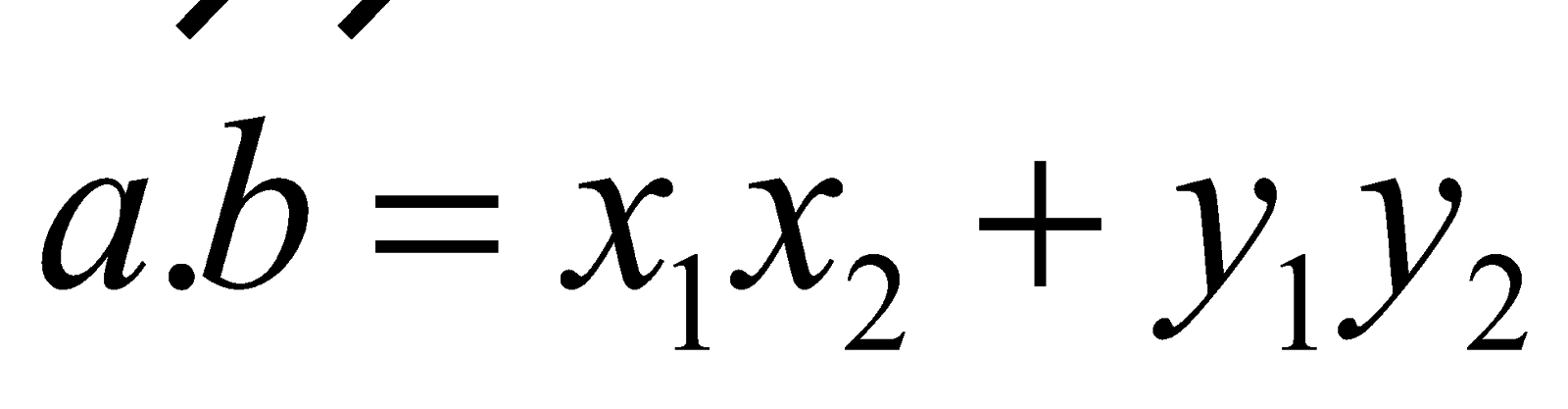
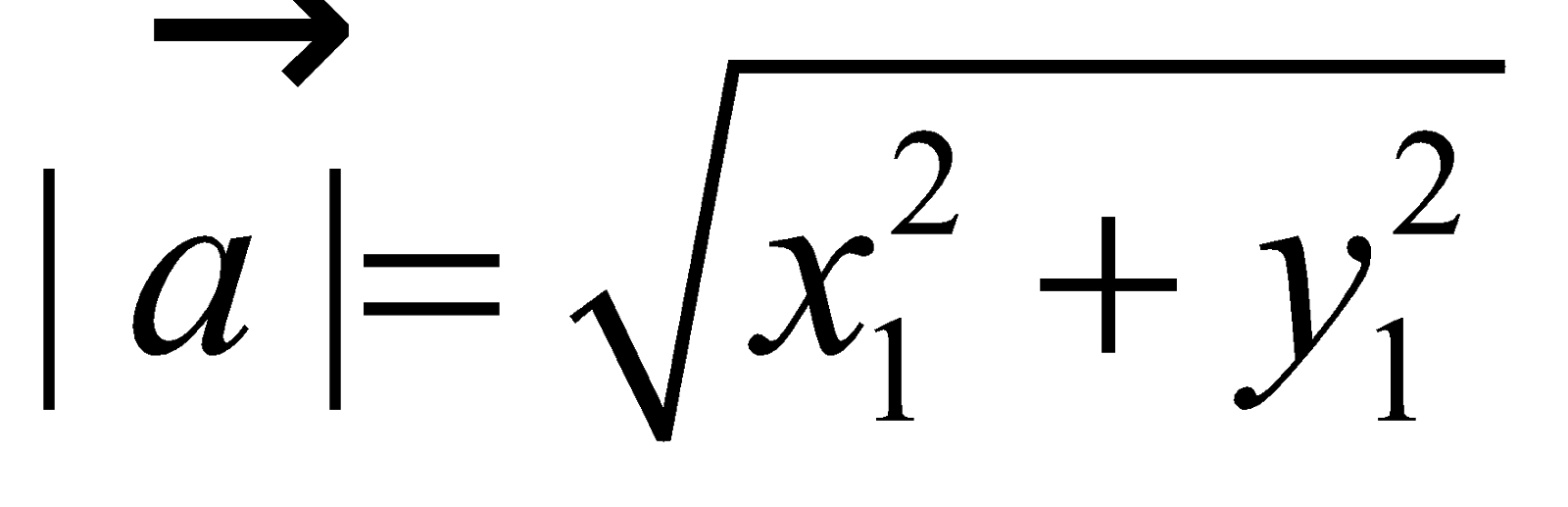
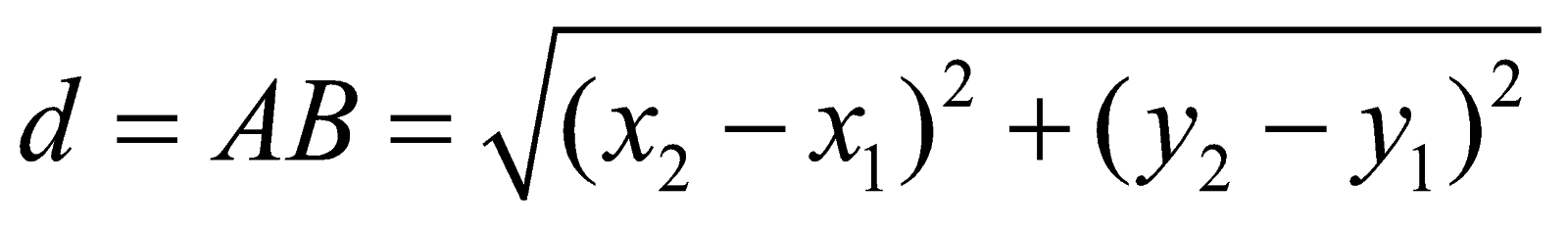
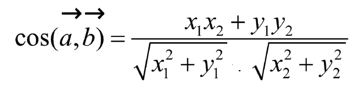
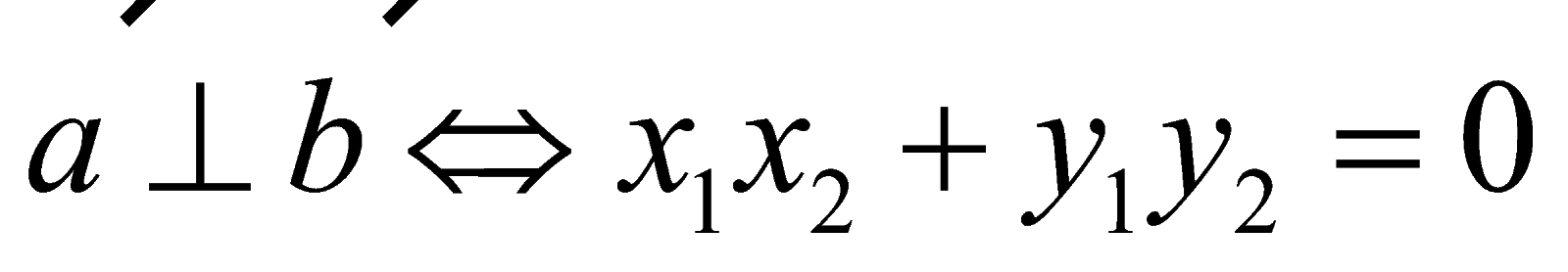
Cho
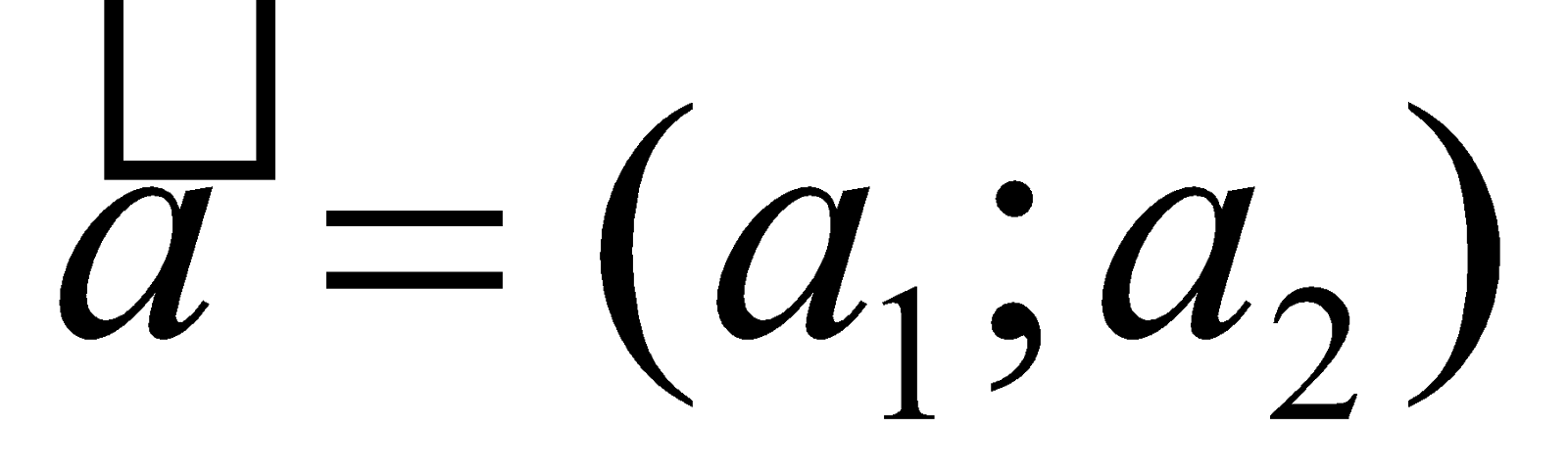
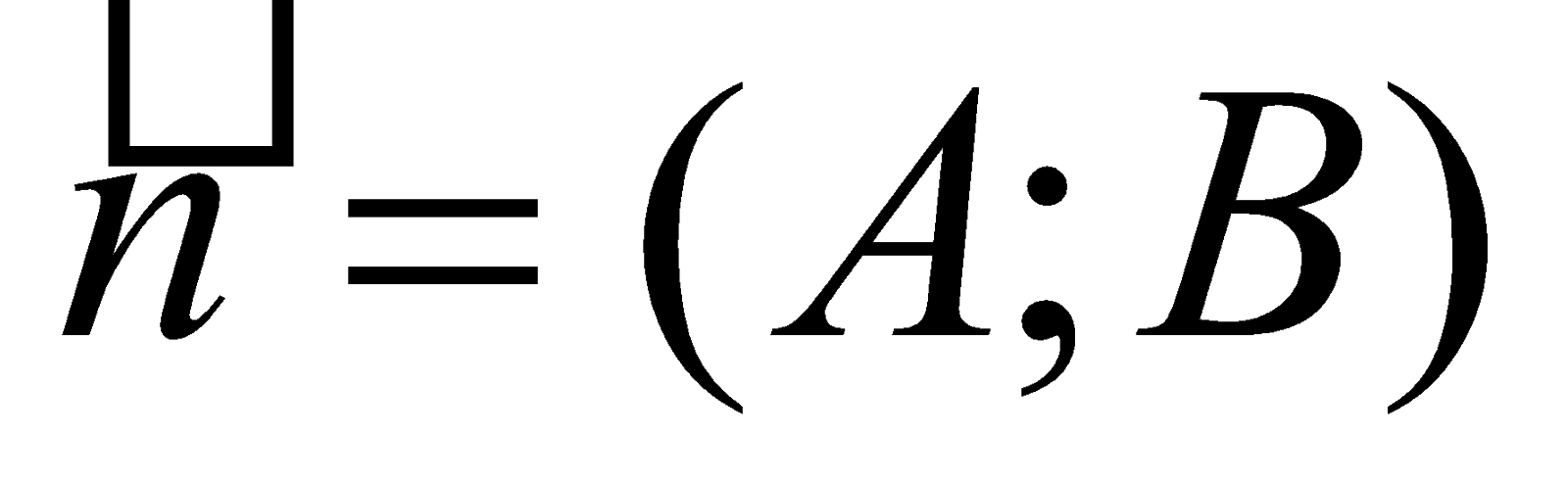
Xem thêm: Đội Vệ Binh Dải Ngân Hà - Lịch Chiếu Vệ Binh Dải Ngân Hà 3
Điểm M(
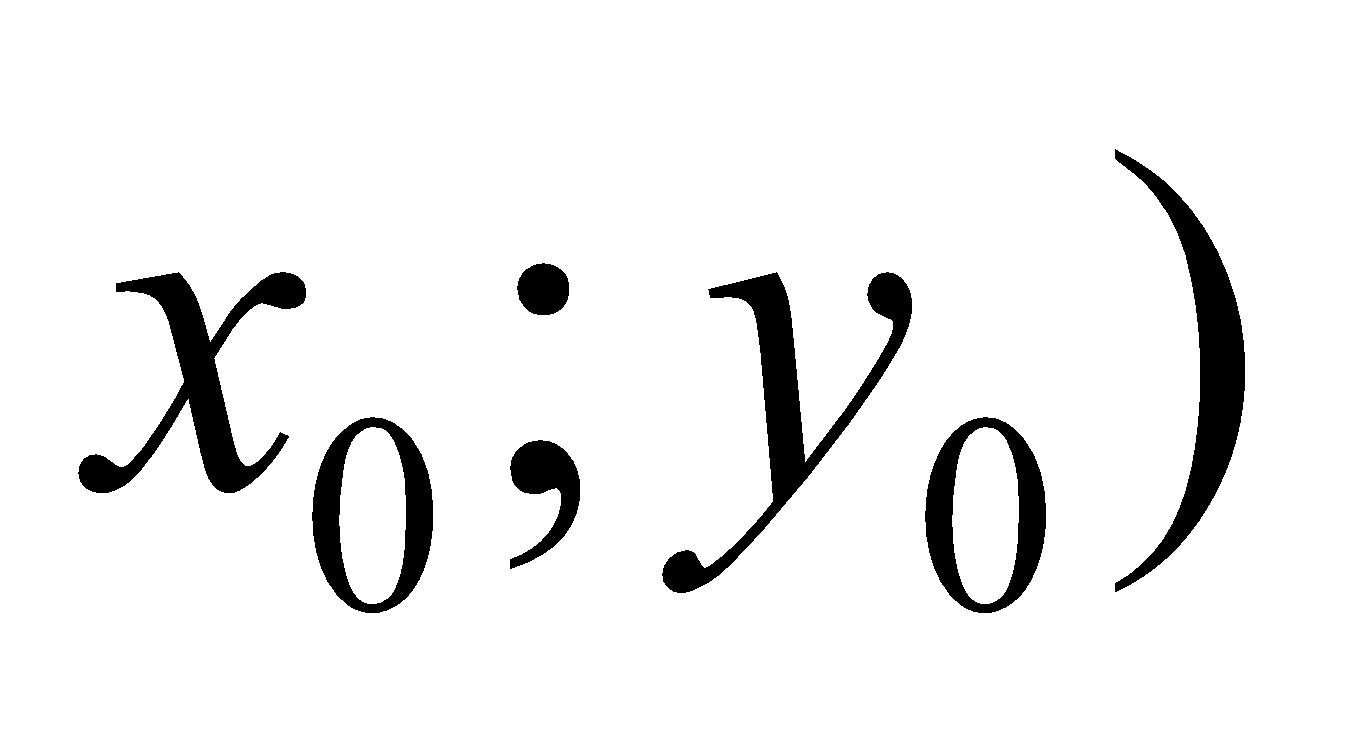
- PT tham số của d:
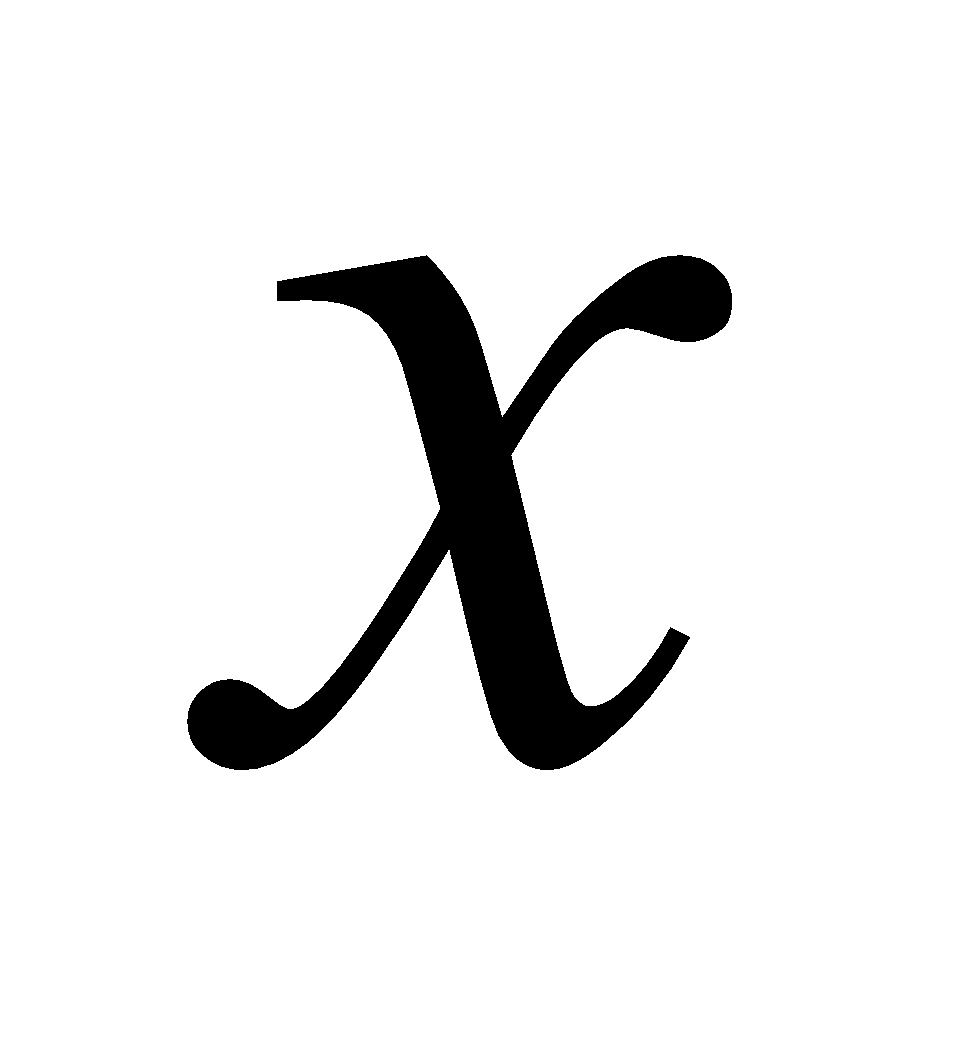
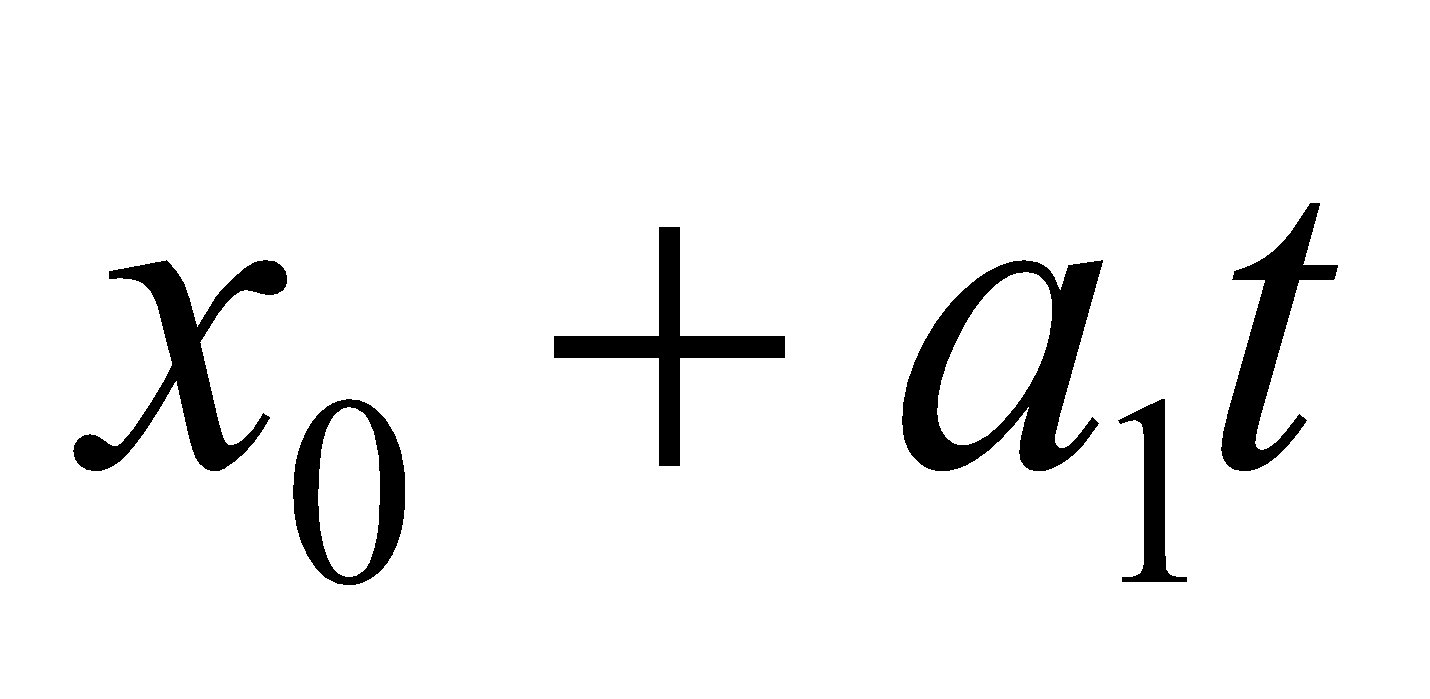
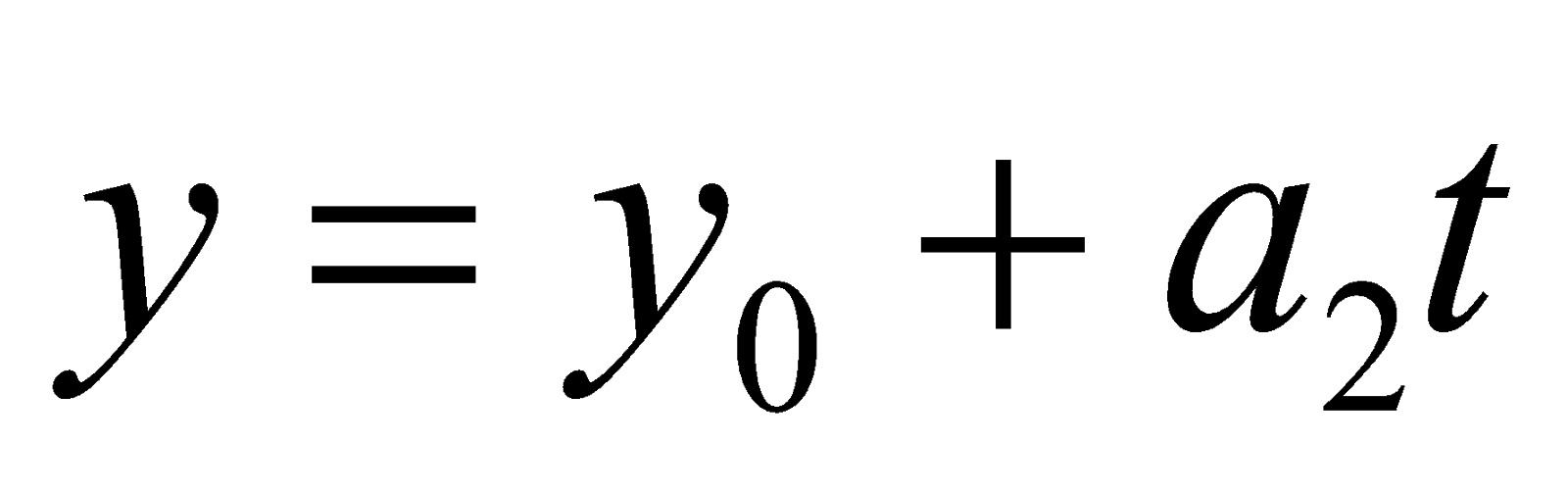
- PT thiết yếu tắc của d:
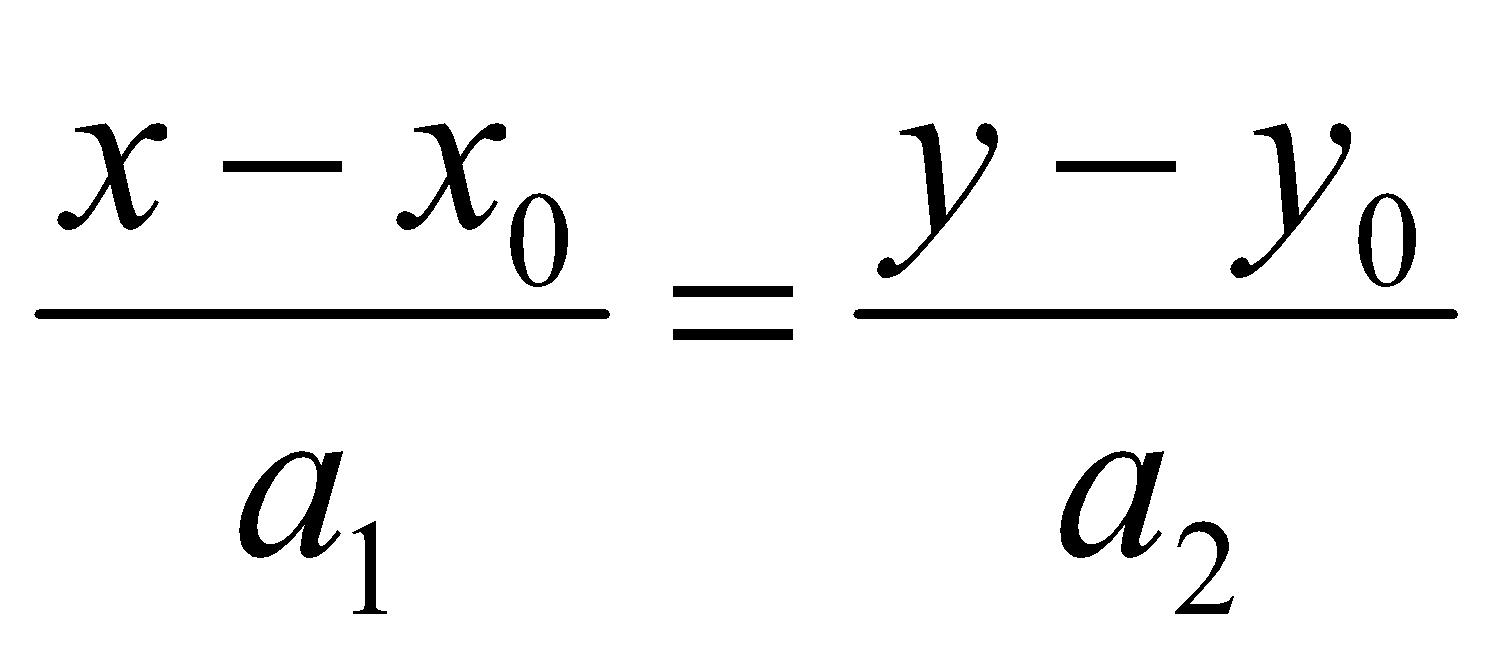
- PT tổng quát của d:
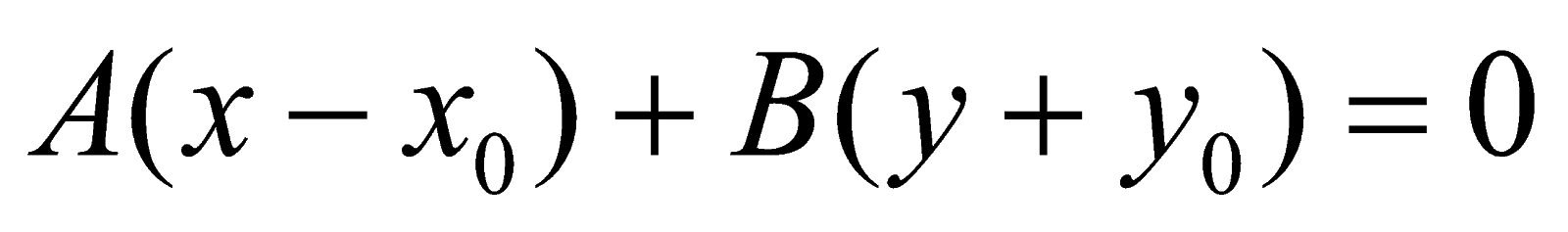
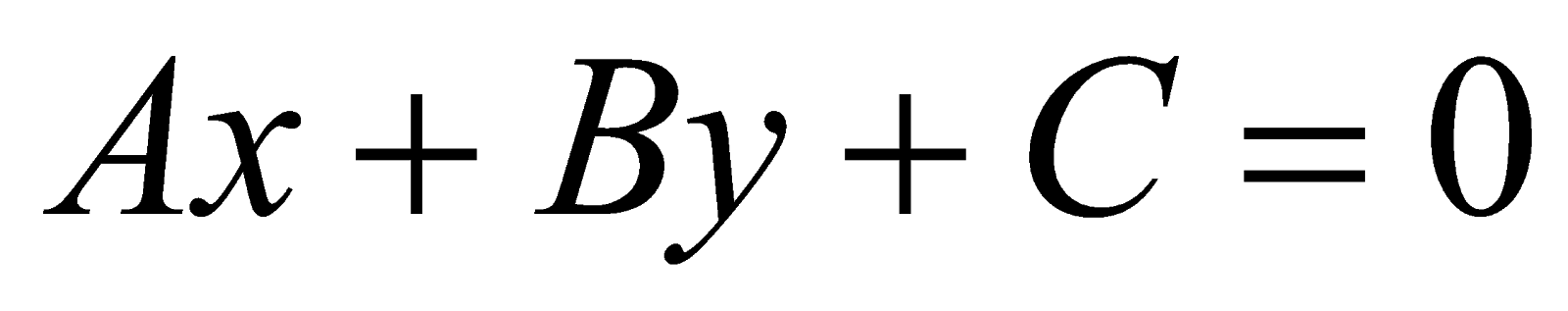
+ khoảng cách từ điểm M(x0, y0) cho đương thẳng (d) : Ax + By + C = 0
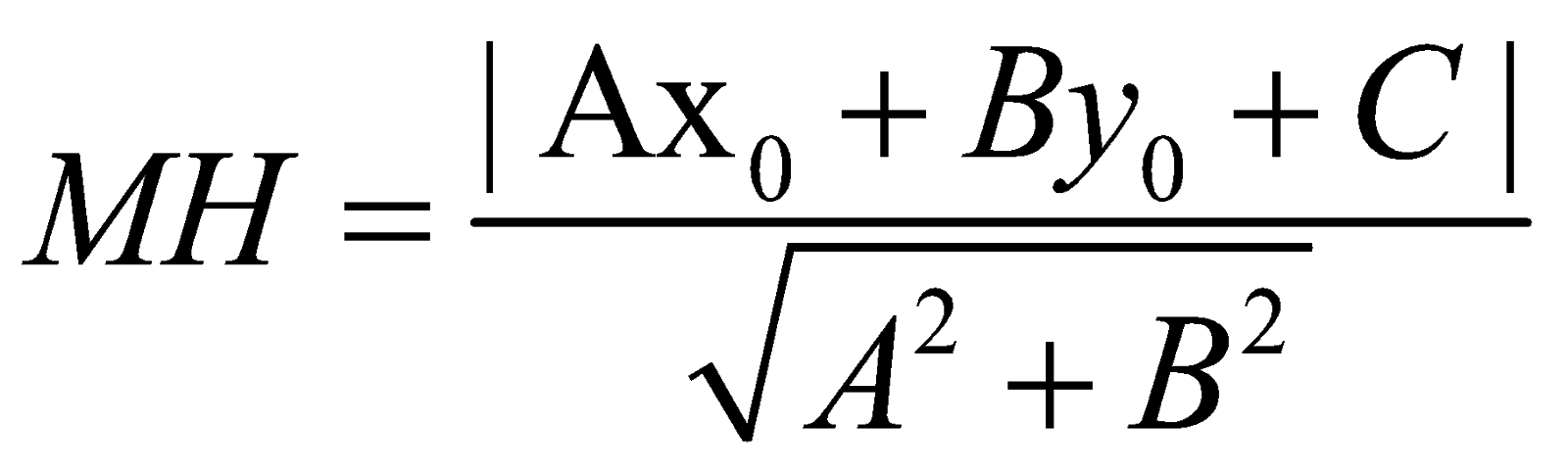
+ khoảng cách giữa hai đường thẳng song song: Ax + By + C1 = 0 với Ax + By + C2 = 0
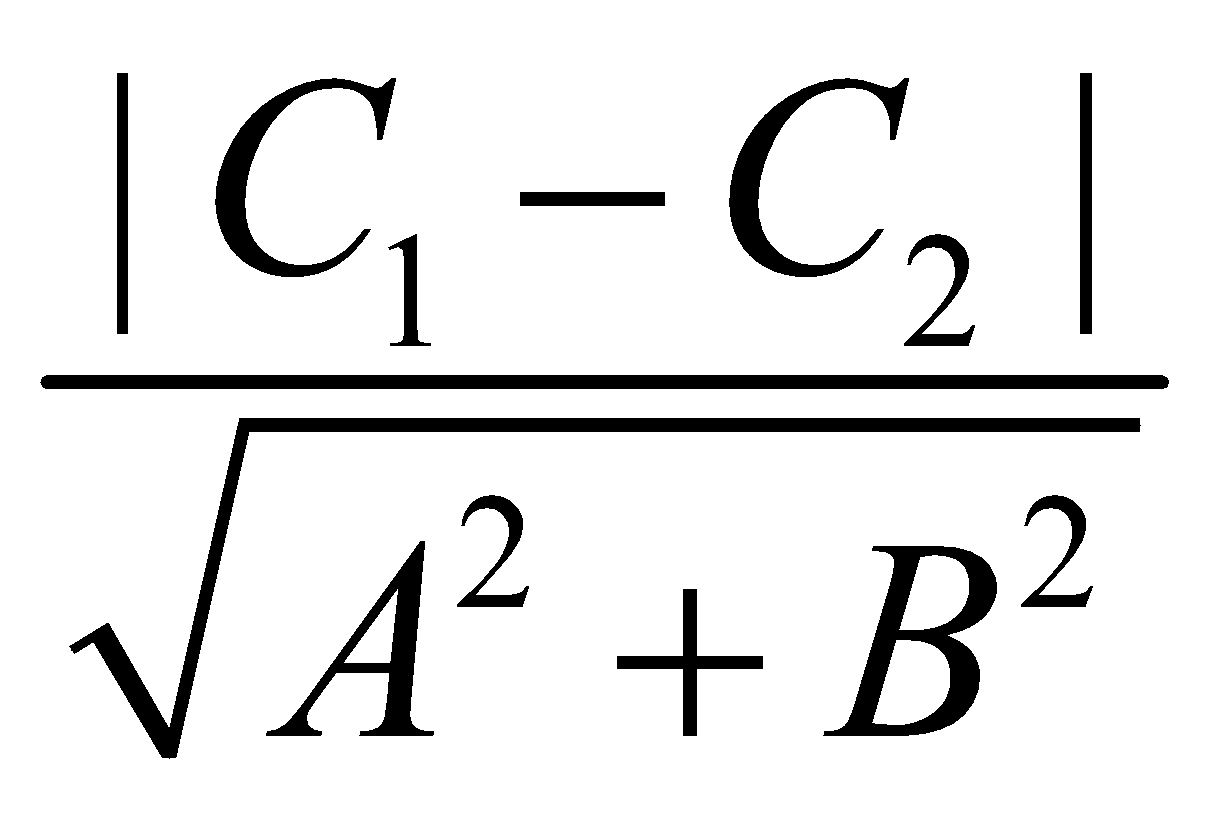
(d1) : A1 x + B1 y + C1 = 0, (d2) : A2 x + B2 y + C2 = 0
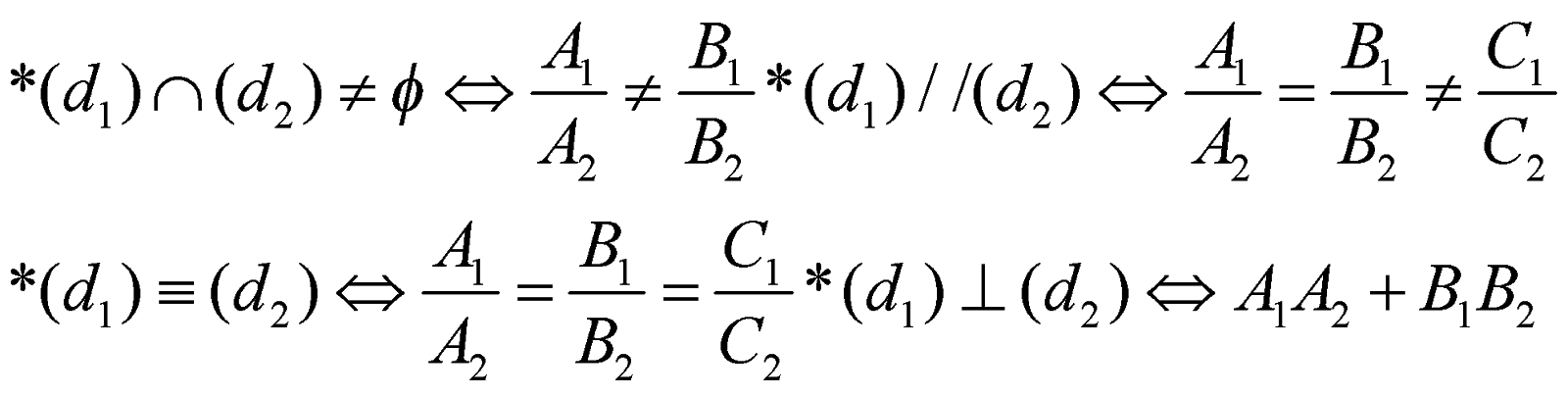
(d1) : A1 x + B1 y + C1 = 0, (d2) : A2 x + B2 y + C2 = 0,
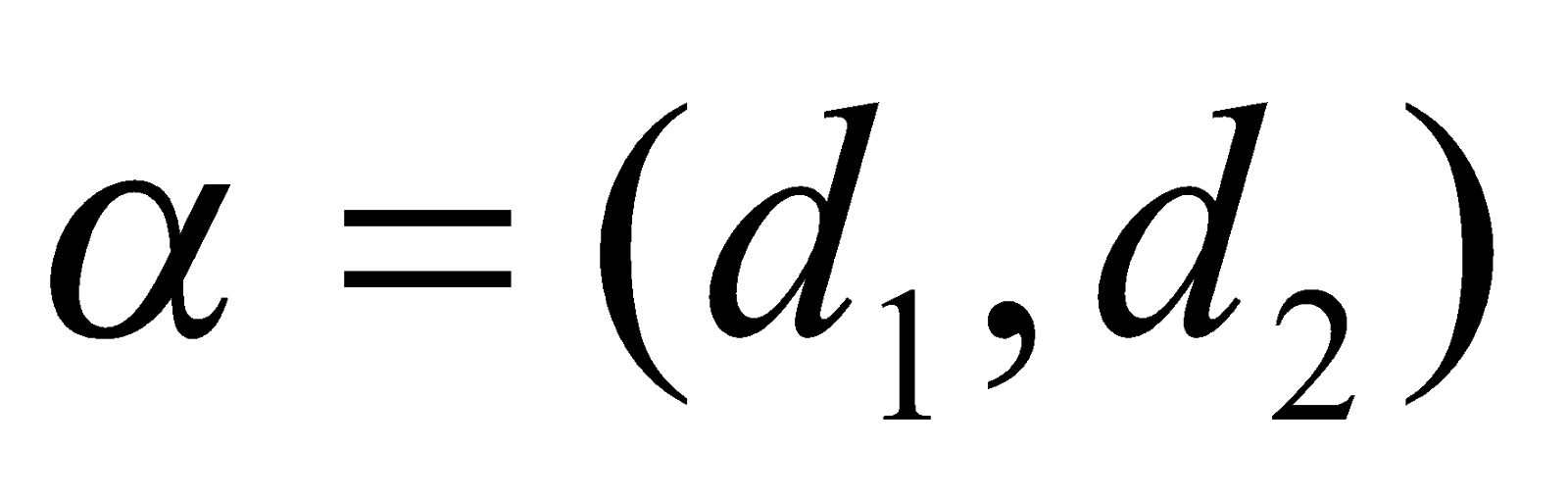
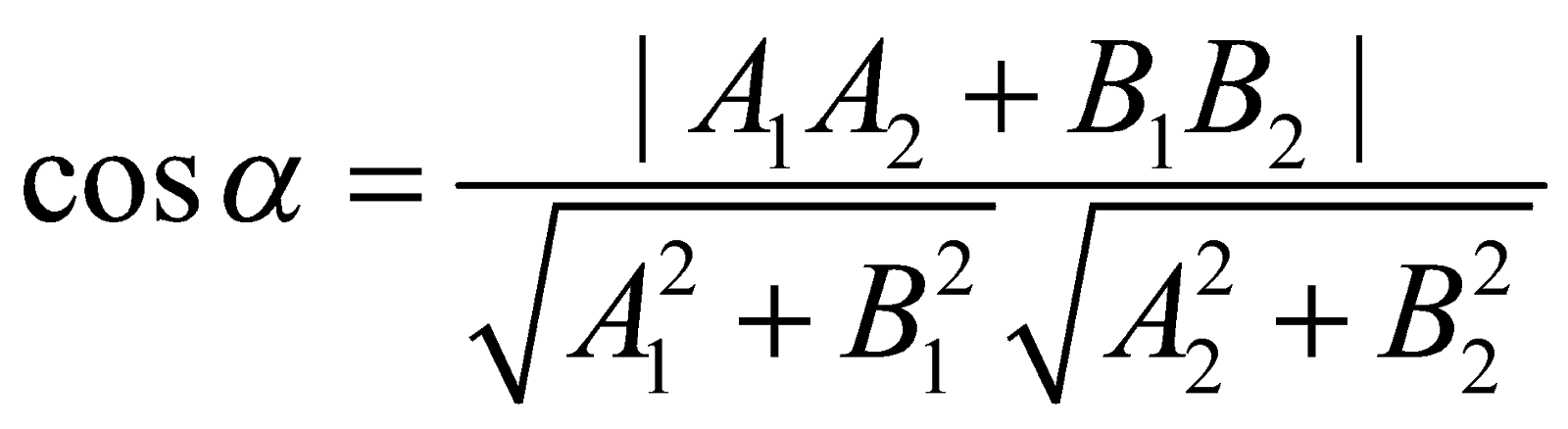
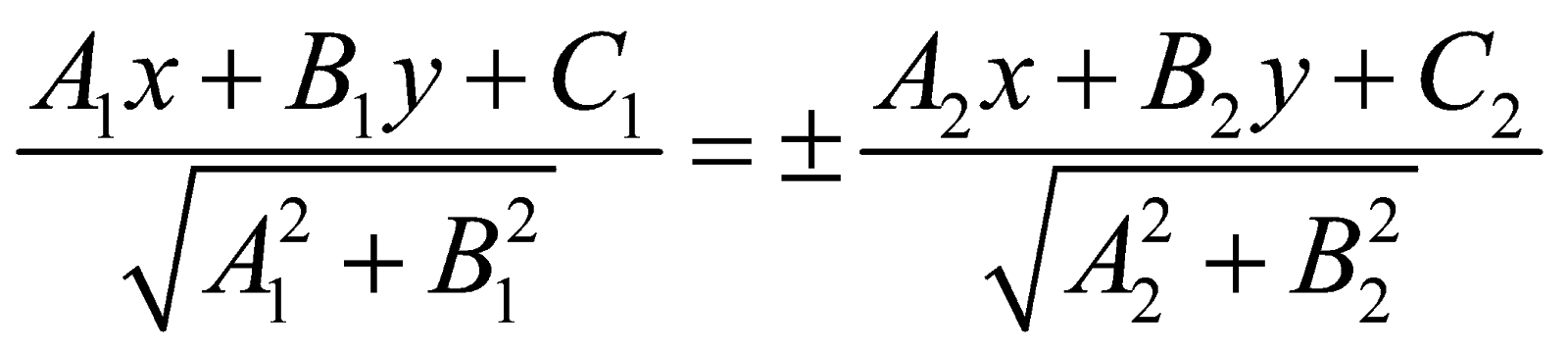
Đường tròn vai trung phong I(a ; b), bán kính R có phương trình :
Dạng 1 :
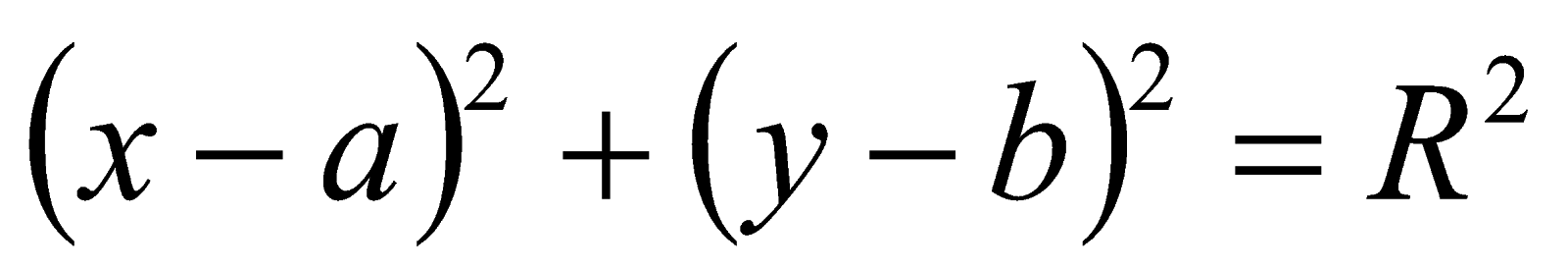
Dạng 2 :
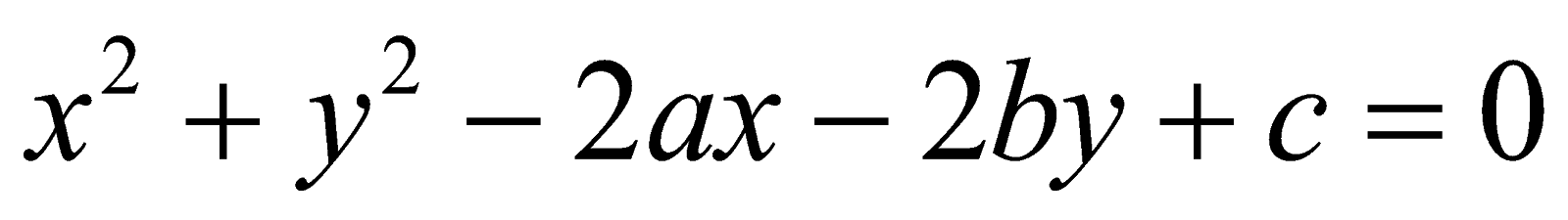
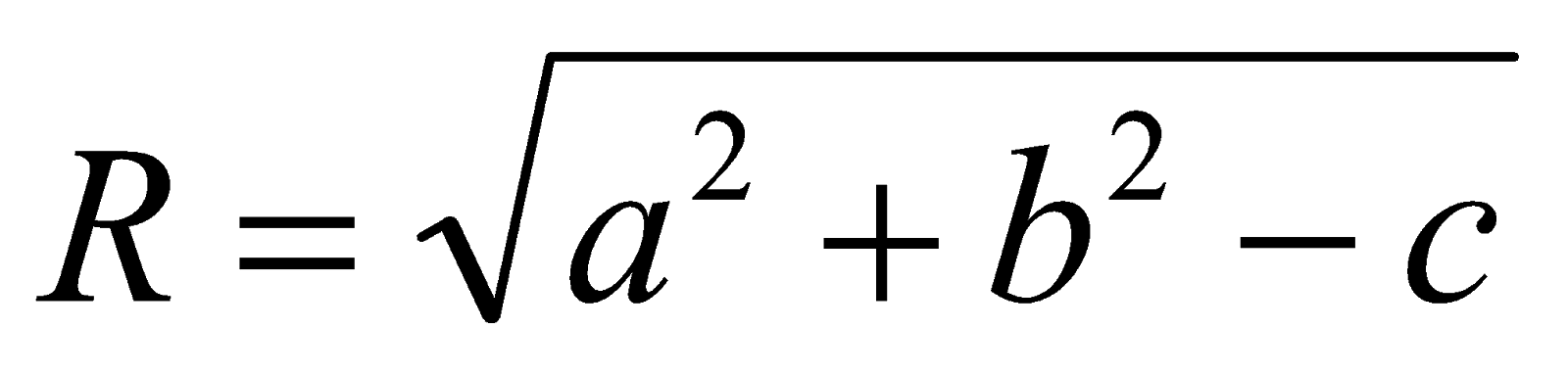
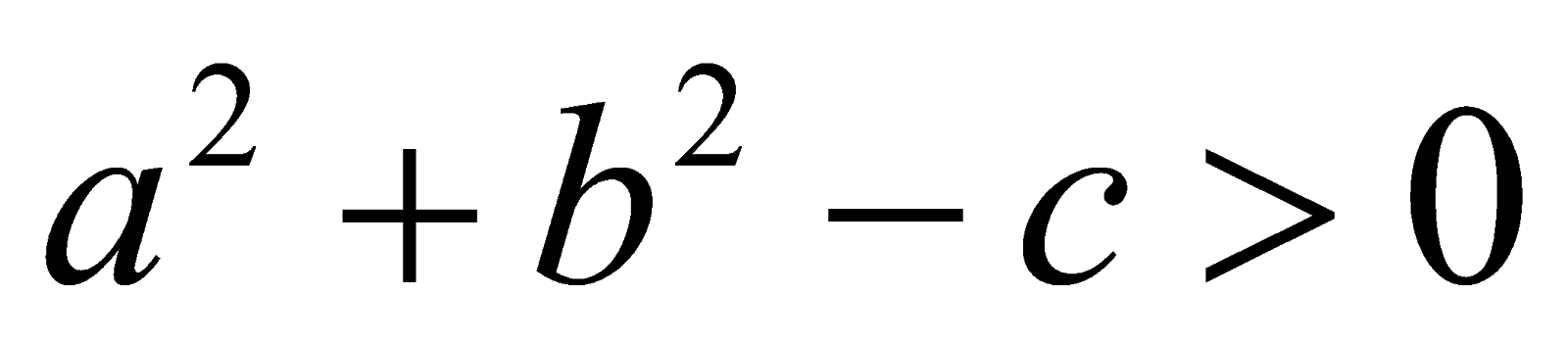
Trên đấy là tài liệu tổng hợp những công thức toán lớp 10 khá đầy đủ các kiến thức và kỹ năng đã học trong công tác toán 10. Những công thức được biên soạn ví dụ theo từng chương, từng bài rất cân xứng để các em học tập sinh thuận lợi học thuộc. Cùng với bộ bí quyết ngắn gọn này, hy vọng sẽ giúp đỡ các em sẽ ôn tập hiệu quả, chấm dứt tốt những bài bác kiểm tra sắp tới của bản thân mình và là người bạn đồng hành cùng những em trong số năm học phổ thông.
Mua tài khoản tcncongdoan.edu.vn Pro để những hiểu biết website tcncongdoan.edu.vn KHÔNG quảng cáo và tải toàn cục File rất nhanh chỉ còn 79.000đ.Tổng hợp kỹ năng Toán lớp 10 gồm 72 trang được soạn bởi người sáng tác Nguyễn Thanh Nhàn. Tư liệu tổng hợp toàn bộ kiến thức, phương pháp giải một số dạng toán thường chạm chán trong công tác Toán 10.
Tổng hợp kỹ năng Toán 10 giúp những em khối hệ thống kiến thức theo từng nhà đề, kèm từ đó là những ví dụ minh họa giúp những em dễ dàng nhớ. Đồng thời tổng hợp kỹ năng Toán 11 cung cấp hệ thống bài xích tập soạn theo nấc độ áp dụng và vận dụng cao. Số lấy ví dụ như nhiều, lời giải chi tiết, dễ dàng hiểu, bài bác tập vận dụng có giải mã sau mỗi công ty đề. Vậy sau đây là trọn bộ cụ thể tài liệu tóm tắt kỹ năng và phương pháp giải Toán lớp 10 mời chúng ta cùng theo dõi tại đây.
Tổng hợp kiến thức Toán 10
1. Mệnh đề
Mệnh đề là một xác minh đúng hoặc sai. Mệnh đề tất yêu vừa đúng vừa sai.
Ví dụ:
i) 2+3 = 5 là mệnh đề đúng.
ii) "

iii) "Mệt thừa l" chưa hẳn là mệnh đề
2. Mệnh đề đựng biến:
Ví dụ: mang lại mệnh đề 2+n=5. Với mỗi quý hiếm của n thi ta được một để đúng họ̆c sai. Mệnh đề như bên trên được điện thoại tư vấn là mệnh đề cất biến.
3. Lấp định của mệnh để:
Phủ định của mệnh đề p. Kí hiệu là



Ví dụ:


4. Mệnh đề kéo theo:
Mệnh đề "nếu


Mệnh đề

Ví dụ: Mệnh đề "

P: mang thiết (điều kiện đủ để có Q)
Q: tóm lại (điều kiện cần để có P)
Ví dụ: Cho hai mệnh đề:
P: “Tam giác ABC bao gồm hai góc bằng 600”
Q: “Tam giác ABC là tam giác đều”
Hãy phát biểu mệnh đề p ⇒Q bên dưới dạng đk cần, điều kiện đủ.
i) Điều kiện cần: “Để tam giác ABC bao gồm hai góc bởi 600 thì đk cần là tam giác ABC là tam giác đều”
ii) Điều khiếu nại đủ: “Để tam giác ABC là tam giác hồ hết thì đk đủ là tam giác ABC cóhai góc bằng 600”
5. Mệnh đề đảo – nhì mệnh đề tương đương.
Mệnh đề đảo của mệnh đề


Chú ý: Mệnh đề


Nếu nhì mệnh đề



6. Kí hiệu 


7. Lấp định của

* Mệnh đề tủ định của mệnh đề “
)
%7D)
* Mệnh đề bao phủ định của mệnh đề “
)
%7D)
Ghi nhớ:
- che định của


- bao phủ định của


- bao phủ định của = là

- lấp định của > là

- phủ định của
+Q(x) là điều kiện cần để sở hữu P(x).
3. Định lí đảo, điều kiện cần với đủ:
Xét mệnh đề đảo của định lí dạng (1) là


Mệnh đề (2) có thể đúng, rất có thể sai. Nếu mệnh đề (2) đúng thì nó được gọi là định lí đảo của định lí (1), thời gian đó (1) hotline là định lí thuận.
Định lí thuận với đảo rất có thể viết gộp lại thành một định lí dạng:
Khi kia ta nói: P(x) là điều kiện cần với đủ để sở hữu Q(x) (hoặc ngược lại). Bên cạnh đó ta cũng nói theo một cách khác “P(x) khi và chỉ còn khi (nếu còn chỉ nếu) Q(x)”









