Trong nội dung bài viết này, hãy thuộc TTnguyen mày mò một số kỹ năng cơ phiên bản cùng với những dạng bài bác tập về ánh xạ con đường tính thường gặp gỡ trong quá trình học đại số và hình học tập giải tích. Bắt đầu thôi!!!
1. Ánh xạ tuyến tính là gì?
Định nghĩa: V→W từ không khí vecto V đến không gian vecto W gọi là ánh xạ con đường tính nếu ưng ý 2 tính chất sau:f(x,y)=f(x)+f(y)f(kx)=kf(x)∀ x, y∈V, ∀ k∈ R
2. Các đặc thù của ánh xạ con đường tính
Cho V và W là hai không gian véc tơ. Giả dụ f: V → W là 1 trong những ánh xạ con đường tính thì:
f(θ) = θf(–v) = –f(v), ∀v ∈ Vf(u – v) = f(u) – f(v), ∀u, v ∈ V.Bạn đang xem: Chứng minh ánh xạ tuyến tính
3. Hạng của ánh xạ tuyến tính – Định lí về số chiều
Định nghĩa hạng của axtt: nếu như f: V → W là 1 trong những ánh xạ tuyến tính thì số chiều của Im(f) hotline là hạng của f, cam kết hiệu là rank(f).
rank(f) = dim(Im(f)).
Định lý về số chiều: giả dụ f: V → W là 1 trong ánh xạ con đường tính thì
dim(Im(f)) + dim(Ker(f)) = n,
trong kia n = dim
V, có nghĩa là rank(f) + dim(Ker(f)) = n.
3. Chứng minh ánh xạ con đường tính
Ví dụ: Cho R2→R3, minh chứng ánh xạ f có phải là ánh xạ tuyến tính hay không?
f(x,y)=(x+y, 0, 2x+2y)
Giải
Lấy 2 vecto ngẫu nhiên thuộc (R^2): (x=(a_1; b_1)) với (y=(a_2,b_2))
– (f(x+y)=(a_1+ a_2,b_1+ b_2))
(= (a_1 + a_2 + b_1 + b_2, 0 , 2a_1 + 2a_2 + 2b_1 + 2b_2))
(= (a_1 + b_1 , 0 , 2a_1 + 2b_1) + (a_2 + b_2 , 0 , 2a_2 + 2b_2) )
(= f(x) + f(y))
– (f (kx) = f(ka_1 , kb_1))
= ((ka_1 + kb_1 , 0 , 2ka_1 , 2kb_1))
= (k(a_1 + b_1, 0 , 2a_1 + 2b_1))
= (kf(x))
Vậy ánh xạ đã cho là ánh xạ tuyến tính.
4. Ma trận của ánh xạ tuyến tính
V là không gian vecto với cửa hàng S
W là không gian vecto với các đại lý T
Ma trận của f theo đại lý S -> T là ma trận gồm những cột là các toạ độ f(s) theo cơ sở T
Cách tra cứu ma trận của ánh xạ tuyến đường tínhTìm hình ảnh f(s)Tìm toạ độ (
5. Bí quyết tìm ma trận chính tắc của ánh xạ tuyến tính
Ví dụ: Tìm ma trận thiết yếu tắc của ánh xạ f: R3→R4
f (a, b, c) = (a + b + c, b, bc, a + c)
Giải
Có thể viết lại thành dạng cột:
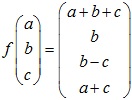
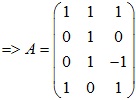
Ví dụ: Tìm ma trận của f theo cửa hàng S-T : R3→R2
f (a, b, c) = (b + c, 2a-c)
S = u 1 (1,0,1), u 2 (4,3,3), u 3 (1,2,1)
T = (2,2), (1,7)
Giải
Tìm ảnh f(s):
f (u 1 ) = f (1,0,1) = (1,1)
f (u 2 ) = f (4,3,3) = (6,5)
f (u 3 ) = (1,2,1) = (3,1)
Tìm toạ độ
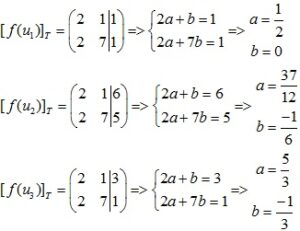
Vậy ma trận S – T là:
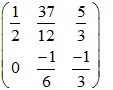
6. Bài tập ánh xạ đường tính gồm lời giải
6.1 bài tập chứng tỏ ánh xạ tuyến tính bao gồm lời giải
Bài 1: Ánh xạ f: R2 → R2 liệu có phải là tuyến tính không?
f (x, y) = (x, y + 1)
Giải
Lấy 2 vecto bất kỳ thuộc (R^2): (x=(a_1; b_1)) cùng (y=(a_2,b_2))
– (f(x+y)=(a_1+ a_2,b_1+ b_2))
= ((a_1 + a_2, b_1 + b_2 + 1))
= ((a_1, b_1 + 1) + (a_2 ,b_2))
≠ f (x) + f (y)
Vậy ánh xạ đã cho không hẳn là ánh xạ đường tính.
Bài 2: Ánh xạ f: R2 → R2 liệu có phải là tuyến tính không?
f (x, y) = (y, y)
Giải
Lấy 2 vecto ngẫu nhiên thuộc (R^2): (x=(a_1; b_1)) với (y=(a_2,b_2))
– (f(x+y)=(a_1+ a_2,b_1+ b_2))
= ((b_1+ b_2, b_1+ b_2))
= ((b_1+ b_1)+(b_2+ b_2))
= (f (x) + f (y))
– (f (kx) = f(ka_1 , kb_1))
= ((kb_1, ka_1))
= (k(b_1, b_1))
= (kf(x))
Vậy ánh xạ đã cho là ánh xạ đường tính.
6.2 tra cứu ma trận f so với cơ sở thiết yếu tắc
Bài 1: kiếm tìm ma trận chủ yếu tắc của ánh xạ f: R3→R3
Bài giảngGiải tích 1Giải tích 2Đại số con đường tính (Linear
Algebra)Xác suất thốngkê
Phương pháp Toán Lý (PT Đạo hàm riêng và PBĐLaplace)Thảo luận
Thảo luận về giảitích
Thảo luận ĐSTTThảo luận XSTKEbooks
Maths Ebooks
Shortlink: http://wp.me/P8gtr-13S
1. Định nghĩa:
Cho V cùng V’ là hai không gian vec-tơ bên trên trường số K. Ánh xạ

(L1):

(L2)

Một ánh xạ tuyến tính đi trường đoản cú V vào chủ yếu nó nói một cách khác là phép thay đổi tuyến tính giỏi toán tử con đường tính trên V.
– dìm xét: từ hai đk trên, dễ ợt nhận thấy rằng:


2. Tính chất:
Cho

1.

2.

Chứng minh:
1. Ta có:

Suy ra:

Mặt khác:

Do đó, từ bỏ (*), (**) ta có:

2. Ta có:

3. Các ví dụ:
3.1: Ánh xạ hằng quý hiếm không:

3.2: Ánh xạ đồng bộ

3.3 Phép rước đạo hàm

Xem thêm: Tinh dầu cà cuống bán ở đâu, cà cuống: nơi bán giá rẻ, uy tín, chất lượng nhất
3.4 Phép mang tích phân xác định:

là một ánh xạ đường tính từ không gian C
3.5: mang lại điểm


4. Tính chất:
4.1 Ánh xạ tích



4.2 qua 1 ánh xạ con đường tính, một hệ vec-tơ nhờ vào tuyến tính lại trở thành 1 hệ vec-tơ dựa vào tuyến tính.
Nghĩa là:



Ngược lại, trường hợp hệ


Chứng minh: do



Suy ra:

Hay:

Vậy tồn tại ít nhất một


Chú ý: Ánh xạ tuyến tính có thể biến 1 hệ chủ quyền tuyến tính thành một hệ phụ thuộc tuyến tính.
5.Định lý cơ bạn dạng về sự xác định ánh xạ đường tính:
5.1 ví dụ mở đầu:
Cho

L(1,1) = (-1,1,2,3)
L(-1,1)=(2,0,2,3)
Tìm f(5,3)? Tổng quát, hãy xác định công thức f(x,y)?
Giải: Ta bộc lộ tuyến tính vec-tơ (5,3) theo nhì vec-tơ (1,1) và (-1,1).
Ta có: (5, 3) = 4(1, 1) – 1.(-1, 1)
Khi đó, do L là ánh xạ tuyến đường tính nên: L(5, 3) = L(4.(1, 1) – 1.(-1, 1)) = 4L(1, 1) – L(-1,1)
Vậy: L(5, 3) = 4.(-1, 1, 2, 3) – (2, 0, 2, 3) = (-6, 4, 6, 9)
Tương tự:

Từ đó, dễ dàng tìm được công thức của L(x,y).
Nhận xét: ta chỉ có thể thể hiện tuyến tính những vec-tơ (x,y) theo 2 vec-tơ (1, 1) với (-1, 1) nếu hệ (1, 1) , (-1, 1) là đại lý của

5.2 Định lý:
Cho một cửa hàng




Ta bảo: ánh xạ đường tính hoàn toàn xác định bởi hình ảnh của một cơ sở.
Chứng minh:
– Sự tồn tại: giả sử x là 1 vec-tơ ngẫu nhiên của V. Lúc đó:

Ta đặt:

Vậy: f là một trong ánh xạ đi trường đoản cú V vào W cùng hiển nhiên

Ta phải chứng minh: f là ánh xạ con đường tính.
Thật vậy vơi đông đảo vec-tơ x, y trực thuộc V. Ta có:

Ta buộc phải chứng minh:

Thật vậy, ta có:

Do đó:

Vậy f là ánh xạ con đường tinh.
– Sự duy nhất:
Giả sử còn trường tồn ánh xạ đường tính


Khi đó: với tất cả


Vậy f = g, giỏi f duy nhất.◊
5.3 các ví dụ:
5.3.1 trong





5.3.2 Trong không khí



Hỏi gồm tồn trên duy nhất hay là không toán tử tuyến tính f (g) trên



6. Nhân (Kernel) và hình ảnh (Image) của ánh xạ tuyến đường tính:
6.1 Định nghĩa:
Cho

Nhân của ánh xạ tuyến đường tính f là tập hợp:

Ảnh của ánh xạ tuyến tính f là tập hợp:

Số chiều của Imf với kerf tương ứng gọi là hạng cùng số khuyết của f, ký hiệu theo lần lượt là rank(f) với def(f). (nghĩa la dim(imf) ≡ rank(f); dim(kerf) ≡ def(f) )









